区域气象特征对流层延迟模型的建设研究

陈中新，朱丽强

(1.苏州工业园区格网信息科技有限公司，江苏苏州 215021； 2.JSCORS苏州分中心，江苏苏州 215021)

区域气象特征对流层延迟模型的建设研究

陈中新1，2，朱丽强1，2

(1.苏州工业园区格网信息科技有限公司，江苏苏州 215021； 2.JSCORS苏州分中心，江苏苏州 215021)

在分析GPS随机软件中两种常用的对流层延迟模型的基础上，利用苏州地区CORS网络数据计算了模型与高度、纬度之间的关系，提出了在网络RTK模式下建立区域气象特征的对流层延迟模型的必要性。

对流层延迟；区域模型；网络RTK

1 引 言

对于城市测绘而言，无论是静态测量，还是实时动态测量，利用站间距比较近而空间误差相关性强的假设，通过观测值之间求差的方法，可以有效削弱GPS信号传播过程中的各种误差。但是由于对流层直接与地面接触并从地面得到能量，其温度随高度的上升而降低、大气层质量的99%集中于此，以及随站间距的增加对流层延迟路径上物理性质不相似越明显的特性，使得GPS信号延迟的80%来源于对流层[1]，因此，在与IGS站联测、高精度GPS基线处理以及气候复杂变化时的实时动态，就不能通过简单求差减弱对流层延迟的影响，必须采用合适的对流层模型进行改正。

2 对流层延迟模型

对流层存在着各种各样的复杂的物理过程，从而不断改变气压、温度、湿度沿高度和水平方向的分布，使得大气折射率随时间和空间而变化[2]。尽管可以采用探空仪探测精确的大气剖面，但因其测量的时间长，而大气结构又随时变化等因素，实践中还是采用经验模型改正、参数估计等方法以减小对流层延迟影响。

测量型GPS的随机软件中对流层处理选项中的模型，应该是具有代表性的常见模型。其中Trimble公司的TGO选项包括:Hopfield，Goad and Goodman，Saastamoinen，Black模型等；Topcon公司的Pinnicale选项包括:Goad and Goodman，分段常数法等；Leica公司的LGO选项包括:Hopfield，Saastamoinen，参数估计等。

2.1 Hopfield模型

Hopfield把对流层的折射对观测值的影响分为干分量和湿分量两部分，其中干分量主要取决于大气的温度和压力，湿分量主要取决于信号传播路径上的大气湿度和高度。引入映射函数，其模型方程为:

其中T为测站的绝对温度，以K为单位；P为测站气压，以毫巴为单位；e为测站水气压，以毫巴为单位；E为卫星的高度角，以度为单位；△trop(E)为对流层折射率改正数，以米为单位。

2.2 Saastamoinen模型

Saastamoinen模型把大气分成三部分:从地面到10 km左右高度为对流层，假设其气温递减率为6.5℃/km；从对流层顶到 70 km左右高度为平流层，假设其气温为常数；70 km以外为电离层。天顶方向干湿延迟分量计算的简约模型为:

公式中符号的意义与Hopfield模型一致，f(B，H)为测站所在纬度和高程的函数。

映射函数可采用Marini连分式映射函数，干湿分量映射函数相同，均为:

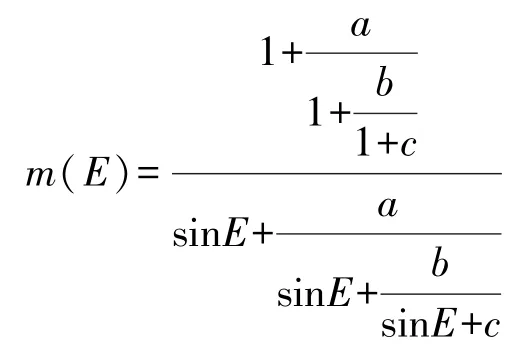
干分量映射函数系数定义为:

湿分量映射函数系数定义为:

3 模型应用的验证与分析

3.1 高精度静态后处理

城市高精度测量控制网都是采用静态测量技术，为了确保成果的质量，一般比规范要求的观测时间增加50%甚至100%，并严格控制观测过程质量，但是往往忽略或不重视基线处理过程中需要的测站气象元素的测定。因此，在没有实测气象元素的情况下，利用加拿大DIPOP软件提供的温度、气压与高度的关系[3]计算模型的延迟量:

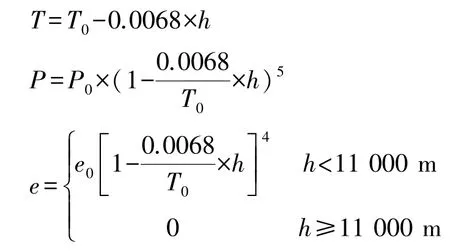
其中T0＝288.15，以度为单位；P0＝1 013.25，以毫巴为单位；e0＝11.691，以毫巴为单位；h为海拔高，以米为单位。因此，对于纬度30°的地区，由于测站高差、不同卫星高度角引起的对流层延迟影响，如表1所示。

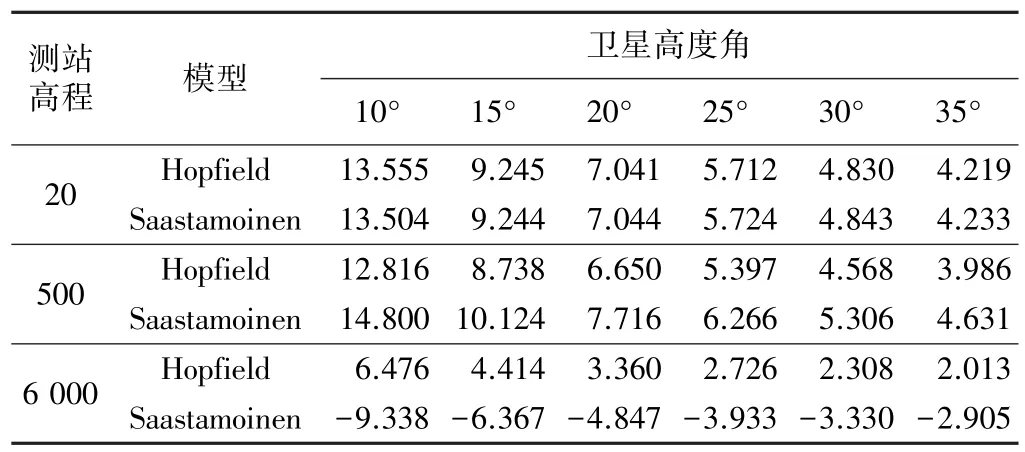
纬度30°地区对流层模型延迟误差(单位/m) 表1

由表1可知，在同一地区(纬度变化不大)，海拔较低时(例如:高程约20 m)在观测高度角不低于15°的情况下，两种典型延迟模型间的误差变化量均在1 cm内。在海拔上升到约 500 m时，两种典型延迟模型间的误差变化量在 50 cm左右。而当海拔为6 000 m时，模型误差间的差值达到几米，甚至十几米。从模型延迟对高度的梯度分析，Hopfield模型的梯度与高度无关，是温度的函数，而Saastamoinen模型与高度有关，随着高度的变化比较明显。随着测站高程的增大，两者之差明显变大。Hopefield模型只按照单层计算，而Saastamoinen模型将温度作为常数分两层计算，并对高度的变化反应灵敏，因此，其精度要比Hopfield模型改正效果要好。

因此，在不同地区进行GPS网数据后处理的时候，要甄别使用合适的对流层模型。近年来，在大型、高精度的GPS控制网数据处理经验，一般采用Saastamoinen模型来估计对流层延迟。为了进一步验证模型间的延迟差异，对苏州地区平均边长约120 km的大型控制网，采用随机软件设置不同大气模型进行基线的处理，其结果如表2所示。可见，在苏州地区使用不同的对流层模型对结果基本没有影响，成果和表1的理论分析相一致。

不同对流层模型对基线解算的影响 表2

3.2 网络RTK实时定位

在常规RTK测量中，由于基站与流动站之间的距离一般控制在10 km范围内，相对于GPS信号的传播路径来说是个微小量，因此，在不使用模型的情况下，直接求双差就能极大削弱对流层延迟。但在网络RTK中，基站的间距达到60 km～100 km，只有当流动站与基准站的距离较近、高差较小的时候，利用差分可以有效减小对流层延迟误差的影响，由于对流层相关性减弱，在大多数时候通过双差不能简单地消除对流层的影响。

由于基站具有全天候、连续观测的特点，系统有足够多的数据来精确求解对流层的天顶延迟参数，从而模拟出区域范围内的大气模型，系统控制中心使用的是根据观测数据不断修正的高精度的对流层延迟模型。但是对于流动站而言，需要通过一两个历元的观测得到高精度的定位，实际上当流动站与基准站的高差超过6 000 m时，如果不修正对流层延迟，由对流层延迟引起的天顶方向延迟偏差达5 m[4]。

对流层延迟的残差对于流动站与CORS网络而言，主要是两者之间的天顶方向相对延迟差，对高程的影响特别显著。它所引起的高程误差[5]:

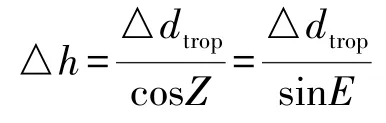
其中△dtrop为天顶方向残余对流层延迟，Z为天顶距，△h为引起的高程误差，E为卫星截止角。根据上式和表1计算在纬度30°的地区，当基站和流动站高差不大的时候，不同模型延迟量的较差对高程的影响，其结果如表3所示；而当基站和流动站高差特别大的时候，同一模型延迟量的较差对高程的影响，其结果如表4所示。

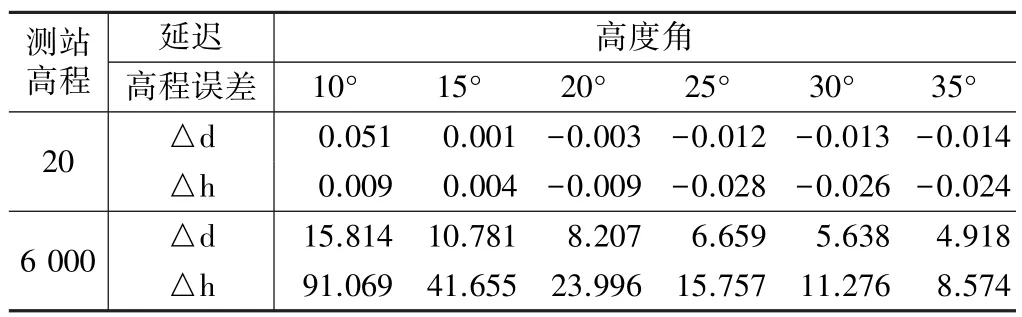
Hopfield和Saastamoinen对流层延迟量之差对高程的影响(单位/m) 表3

Hopfield模型计算对流层延迟量对高程的影响(单位/m) 表4

由表3可知，在低海拔地区，流动站与参考站的高差不大的情况下，即使采用不同的对流层延迟模型所引起的高程误差也在厘米级；而在高海拔地区当采用不同模型时所引起的高程误差可能达到几十米。由表4可知，当流动站与参考站之间的高差达到 6 000 m，即使采用同一对流层延迟模型改正，所引起的高程误差也要有十几米。

因此，即使在网络RTK中的短基线解算也必须谨慎处理对流层延迟误差，从而提高实时RTK的精度和成果的可靠性，原先的一些经典模型改正，其静力学延迟部分的改正精度可以达到厘米级，而湿延迟部分的残余影响还比较大，一般仍会有数厘米的残差。所以，非常有必要在多部门联建的省CORS系统的基础上，通过对对流层延迟随时间的变化随机模型[6]，自主修正高程偏差的距离相关对流层网络内插模型[7]以及用随机游走方法来估计对流层延迟残差[8]等方法的实践和优化，得到符合区域大气条件的对流层延迟模型，从而提高实时定位精度和成果的可靠性。

5 结 论

尽管连续参考站系统已被国内公认为城市基础设施之一，网络RTK技术能实时获取高精度的点位坐标而具有非常广阔的前景，但是对于这一新兴的GPS差分技术，有必要进行系统而严密的研究。从目前的一些测试和实践表明，一方面对流层延迟误差仍是该技术的主要误差源之一；另一方面由于基准站和流动站获取的数据量以及精度要求不同，因而对流层改正模型也应有差异。

因此，建立精确的区域对流层延迟改正模型越来越必要和迫切，这就需要我们创新性地研究对流层延迟对GPS测量的影响，通过各种模型的比较分析，找出修正对流层延迟较为有效的方法，建立起区域气象特征对流层延迟模型，从而可以提高网络RTK成果可靠性、改善高精度基线处理的数据归算，以及优化基于CORS系统的高精度GPS数据仿真。而近年来由测绘局、气象局、地震局等部门联合建设的GPS连续观测网络，比如江苏CORS[9]，能提供的观测数据类型越来越全面，为研究反演计算GPS信号在对流层中传播的时延，建立区域气象特征的对流层延迟模型提供了有利的条件。

[1]霍夫曼－韦伦霍夫，利希特内格尔，瓦斯勒.程鹏飞，蔡艳辉等译.全球卫星导航系统[M].北京:测绘出版社，2009

[2]谢益溪，J拉菲涅特，JP蒙等.电波传播—超短波、微波、毫米波[M].北京:电子工业出版社，1990

[3]曲伟菁，朱文耀，宋淑丽等.三种对流层延迟改正模型精度评估[J].天文学报，2008(1):113～122

[4]何海波.高精度GPS动态测量及质量控制[D].博士学位论文.中国人民解放军信息工程大学，2002

[5]U.Hugentobler，S.Schaer，P.Fridez.Bernese GPS Software (Version 4.2)[M].Stronomical Institute University ofBerne.2001

[6]邵占英，葛茂荣，刘经南.GPS定位中对流层折射率随机模型的研究[J].地壳形变与地震，1996，16(2):1～7

[7]熊永良，黄丁发，丁晓利等.虚拟参考站技术中对流层误差建模方法研究[J].测绘学报，2006，35(2):118～121，132

[8]刘经南，叶世榕.GPS非差相位精密单点定位技术探讨[J].武汉大学学报:信息科学版，2002，27(3):234～240

[9]安艳辉，史照良.全球卫星导航定位连续运行参考站网的技术探讨——以JSCORS徐州试点工程为例[J].现代测绘，2006，29(6):3～6

Research on the Modeling of Tropospheric Delay Based on a Region Atmosphere Features

Chen ZhongXin1，2，Zhu LiQiang1，2
(1.Suzhou Industrial Park Geone Information Technology CO.，Ltd.Suzhou，215021，China；2.JSCORS Suzhou Center，Suzhou 215021，China)

This paper bases on analysing the two familiar tropospheric delay model，using the SZCORS date to prove the relationship between altitude and latitude.Then It indicates the necessary to build the modeling of tropospheric delay based on a region atmosphere features.

tropospheric delay；region model；network RTK

1672－8262(2010)04－93－04

P228

A

2009—11—23

陈中新(1974—)，男，高级工程师，研究方向:为GNSS连续运行参考站系统的建设、应用及相关领域的研发。

现代工程测量国家测绘局重点实验室经费资助项目(TJES0907)