重力坝坝基面应力规律及扬压力影响分析

某水电站枢纽的非溢流重力坝为 2级建筑物,坝高 72m,坝顶宽 8m,坝底宽 60m,上游边坡系数 m=0,下游边坡系数 m=0.84,如图 1所示。坝基面高程为 470.00m,坝上游设计水位为540.00m,坝下游无水。坝体材料为混凝土,弹性模量为 18.0GPa,泊松比为 0.2,容重 γp=2.40t/m3,地基的弹模为 20.0GPa,泊松比为 0.2,容重γp=2.60t/m3。坝体混凝土材料的抗压强度为5MPa,抗拉强度为 0.65MPa。本文采用结构模型应力试验和基于 ANSYS软件的有限元分析法,分别研究该坝在基本荷载组合下,处于弹性范围内时,坝基面的主应力值和应力分布规律,判断坝基面的应力是否满足设计要求。模型试验法由于受试验条件所限,没有模拟扬压力,有限元分析法对模拟有扬压力和没有扬压力两种情况进行了计算。针对以上三种情况进行比较,分析了试验结果和原因。

图 1 大坝剖面

1 结构模型试验

1.1 模型试验的基本原理及相似定律

基本原理:结构模型试验主要是确定在外荷载作用下,施工建筑物表面和内部的应力及位移分布状态。首先按模型规律选择材料及适当的比尺,做成相似的模型,再把作用在原型水工建筑物的各项荷载按一定的相似比换算成相当的荷载加在结构模型上,然后通过各种量测仪器,测量出模型的应变、位移等数据;最后根据模型相似律,将所测数据换算为原型相应的数据,得到原型水工建筑物在外荷载作用下的应力和位移。

相似定律:为使模型上产生的物理现象与原型相似,模型材料、模型形状和荷载的必须遵循一定的规律,这个规律就是相似定律。在原型和模型两个系统中,存在有几何相似、物理相似、力学相似等。选定线形度量 L和力的度量 P这两个自变量作为基本量,推导出原型和模型其它各量之间的关系。设 C代表相似比,脚标“p”代表原型,脚标“m”代表模型,Lp、Lm分别表示原型与模型的线性量度,Pp、Pm分别表示原型与模型力的量度,则:

应力结构模型试验要求模型材料为线弹性材料。本试验采用纯石膏材料,模型比尺为 180,原型弹模为 18GPa,模型弹模为 2.5GPa。故 GL=18.0,CE=7.2,Cσ=7.2。

1.2 模型试验及成果分析

试验重点考虑坝体的自重和水沙荷载,由于纯石膏较轻,不能满足容重相似的条件,故需要施加外力来实现重力荷载相似。试验中,在坝段重心处采用拉杆挂砝码的方法来弥补重力荷载不足;水荷载采用油压千斤顶(WY-300/V型自控油压稳压装置供压)来施加;千斤顶通过传压板多次传压,使荷载有效地传递到坝面。由于在结构模型中扬压力模拟受限,因而不做模拟。

在坝基处上下游边缘各布置一点,在截面中部再布置三个测点,每个测点布置三片互成 45°的直角式应变片(如图 2所示),背面相同位置处也布置了同样的直角式应变片,用正反两面应变值取加权平均,减少误差。并采用万能数字测定装置 UCAM-70A测量应变,最终得到 5个测点的 15个应变值。由材料力学的知识可知,模型测点 x方向 (即 0°方向)和 y方向(即 90°方向)的应力为:

图 2 重力坝模型试验照片

通过上面计算所得的模型应力,需根据相似定律换算成原型应力,结果如表 1所示。结合 α方向绘出该坝段的主应力分布图,如图 3所示,测点编号从坝踵到坝趾分别为 1、2、3、4、5。最大压应力 2.1607MPa,小于混凝土抗压强度 5MPa,故该坝基面的应力满足设计要求。

图 3 模型试验重力坝坝基面应力分布

表 1 模型试验法坝基面主应力成果单位:MPa,拉为正,压为负

2 ANSYS有限元计算

2.1 有限元数值模拟方法

有限元数值模拟方法,是把弹性的连续体离散化为有限数目的单元组合体,并考虑组合体内单元之间的位移连续条件,综合考虑各种因素的影响作用。采用 ANSYS软件对重力坝坝基面进行应力分析,为了与模型试验法比较,分别对有扬压力和无扬压力两种情况进行模拟计算。当岩体材料处于弹性状态,有下列本构关系:

对于各向同性体,弹性矩阵 [D]取决于下式:

2.2 模型的参数与建模

重力坝坝体和坝基的基本资料和设计参数与模型试验相同,三维有限元模型的范围也与模型试验相同。即上游取 1.5倍坝高,下游取 2倍坝高,铅直向取 1倍坝高,坝段宽度 30m。建模直接采用 CAD平面模型导入方式,经过布尔运算中的EXTRUDE＞AREA命令将二维平面模型拉伸为三维模型。

对于坝基岩体,我们采用三维实体单元 Solid45进行模拟;对坝体混凝土则采用 ANSYS专门的混凝土单元 Solid65进行模拟。坝体坝基材料均为线弹性且各项同性材料,根据概述中的实际资料,坝体的弹模(EX)为 18GPa,泊松比(PRXY)为 0.2,密度 (DENS)为 2.40t/m3,坝基的弹模(EX)为 20GPa,泊松比 (PRXY)为 0.2,密度(DENS)为 2.60t/m3。

网格划分时采用三维体映射划分网格,均为8节点四边形网格。划分好以后的网格图如图 4所示。

图 4 重力坝网络划分图

2.3 计算成果分析

在坝基左右两侧(上下游边缘)施加水平向约束(Ux),坝基底部边界施加铅直向约束(Uy),坝段纵向约束(Uz)。基本荷载的施加分为两个工况:step1包括自重应力场和上游面水压力;step2包括自重应力场、上游面水压力和坝基面上的三角形扬压力。

通过计算,得到各节点的主应力 σ1、σ2。为了与模型试验比较,取出对应于模型试验法中的坝基面 1、2、3、4、5点的主应力值 (如表 2所示 ),绘制坝基面主应力图(如图 5、图 6所示)。

表 2 ANSYS有限元分析坝基面主应力成果单位:MPa,拉为正,压为负

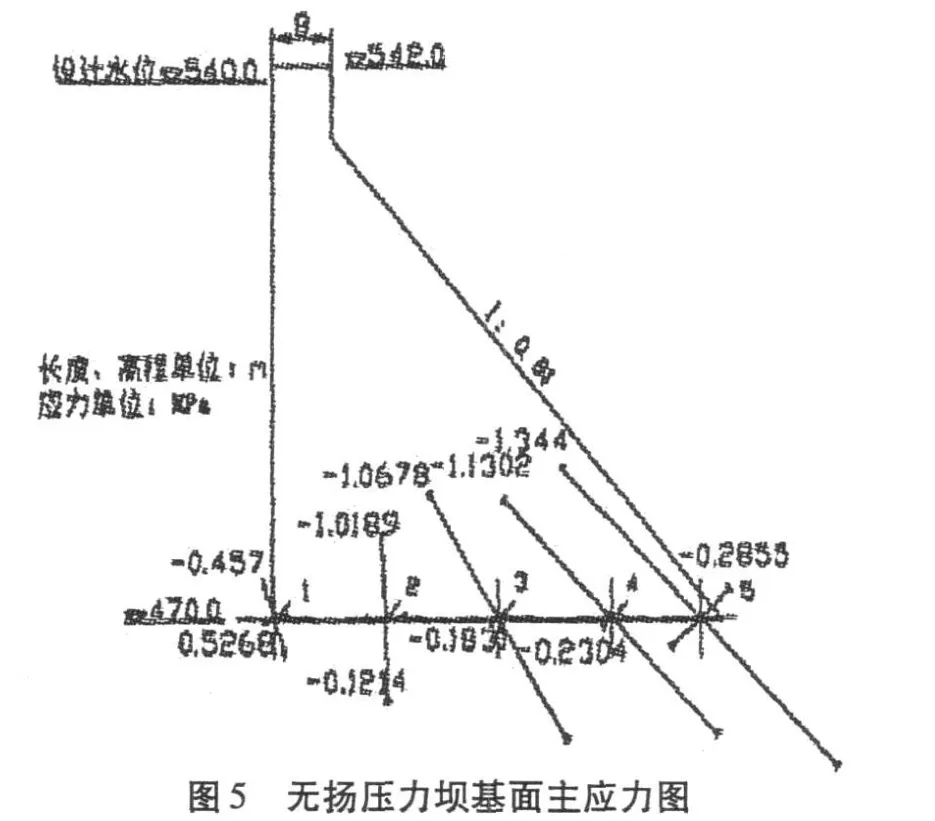
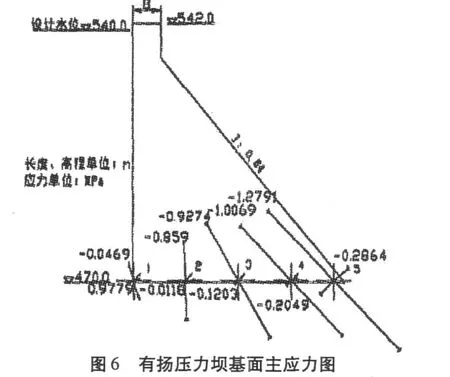
通过图 3、5、6的比较,可以看出结构模型试验法和有限元分析法的结果在坝基面上应力分布规律相似,数值相近。坝基面的主压应力值从坝踵向坝趾逐渐增加,模型试验法中坝踵处主压应力值较小,有限元分析法中坝踵处出现较小主拉应力,两种方法中坝趾处都出现较大主压应力。通过上述图 5、6的比较,可以看出在有限元分析计算中,不施加扬压力的坝基面主应力值总体比施加扬压力后的坝基面主应力值大,这是因为扬压力的方向与自重的方向相反,相互有所抵消。通过图 3、5的比较,可以看出在都不模拟扬压力的情况下,模型试验法得出的坝基面最大主应力值比有限元分析法得出的结果略微偏大。

3 结论

3.1 结构模型试验法和有限元分析法的结果在坝基面上应力分布规律相似,数值相近,坝基面的主压应力值从坝踵向坝趾逐渐增加。模型试验法中坝踵处主压应力值较小,有限元分析法中坝踵处出现较小主拉应力,坝趾处在两种方法中都为较大主压应力。

3.2 模型试验法计算表明,坝基面最大主压应力值为 2.1607MPa,有限元分析法计算表明,坝基面最大主压应力值 1.3440MPa,均小于混凝土抗压强度 5MPa,故该重力坝坝基面的主应力满足设计要求。在有限元分析计算中,没有施加扬压力比施加了扬压力的应力计算结果偏大,这是因为扬压力的方向与自重的方向相反,相互有所抵消。

3.3 结构模型试验法模拟扬压力有一定困难,需要我们从方法和技术上进行改进,同时它与有限元数值计算分析相互补充、相互验证。两种方法都是分析坝基面应力的有效手段。

〔1〕张 林,陈建叶.水工大坝与地基模型试验及工程应用.四川:四川大学出版社,2009.

〔2〕吴媚玲.水工建筑物.北京:清华大学出版社,1981.

〔3〕张 林.碾压混凝土断裂实验研究.水力学报,2001,(5).

〔4〕杨宝全等.重力坝结构模型试验研究.四川水利,2007,(1).

〔5〕陈兴华等.脆性材料结构模型试验.北京:水利电力出版社,1984.

〔6〕陈胜宏.水工建筑物.北京:中国水利水电出版社,2004.

〔7〕陈 媛,张 林等.基于相似理论的重力坝扬压力等效模拟方法研究.四川大学学报(工程科学版),2008.

〔8〕李芬花等 .基于 ANSYS有限元的混凝土重力坝坝踵正应力分析.水利水电技术,2009.