基于协方差矩阵和小波变换的角点检测算法
2010-04-11黄华川张浬萍
黄华川,张浬萍
HUANG Hua-chuan, ZHANG Li-ping
(西南科技大学 制造学院,绵阳 621010)
基于协方差矩阵和小波变换的角点检测算法
A corner detection algorithm based on covariance matrix and wavelet transform
黄华川,张浬萍
HUANG Hua-chuan, ZHANG Li-ping
(西南科技大学 制造学院,绵阳 621010)
角点在机器视觉方面起着十分重要的作用。本文通过对曲线的协方差矩阵构建方向角函数,对该方向角函数在不同尺度下进行小波变换,最后根据小波变换的响应值,找到曲线上的角点。实验结果表明,该算法在一致性和准确性都有较好的表现。
小波变换;角点检测
0 引言
物体的角点包含丰富的信息,且角点的数目远远小于图象中像素点的数目。通过对角点这一局部特征进行处理来替代对整幅图象进行处理,大大地提高了计算速度,使得对图象的实时处理成为可能。此外,由于角点具有旋转不变性和几乎不受光照条件的影响等特征[1],因此,角点具有可以在图象之间进行可靠的匹配等优点,使得角点检测在光流计算、目标跟踪、三维场景重构、运动估计、摄像机标定、视觉的定位和测量等机器视觉方面起着十分重要的作用[2]。
A.Rosenfeld和L.Kitchen利用曲线上一点前后臂夹角的余弦值来估计该点的曲率,将曲线上的局部曲率最大点作为角点[3]。Fei Shen和Han Wang利用Hough变换来检测角点,将图象投影到Hough空间,通过阈值技术检测角点[4]。H.Moravec把角点定义为各个方向上灰度变化足够大的点[5]。文[6,7]是把曲线边缘上的点的方向角函数在多尺度小波变换下同时出现最大值的点作为角点。
1 基于小波变换的角点检测原理及算法
利用小波变换求取曲线角点的实质是用多个高斯低通滤波器对曲线的方向角同时进行滤波,计算曲线的曲率,通过求局部极值,得到候选角点,然后对候选角点进行分类,再采取不同的原则加以判断,最后得到正确的角点。经典方法是利用曲线上某一点前后两点连线与横轴的夹角来构造方向角函数[7],该方法只考虑了曲线上某一点邻域前后两个不同点的信息,舍弃了这两个点之间其他点的信息,考虑的因素不够完善,存在检测出伪角点的可能。
基于协方差矩阵特征向量的小波变换角点检测算法[6],首先计算每个像素一个邻域上的协方差矩阵;然后由该矩阵及其特征值构造方向角函数;最后对该方向角函数进行小波变换,得到角点的位置。该方法的具体检测过程如下:

参数s决定了Pi参与计算的像素个数,n为封闭曲线上像素数目。

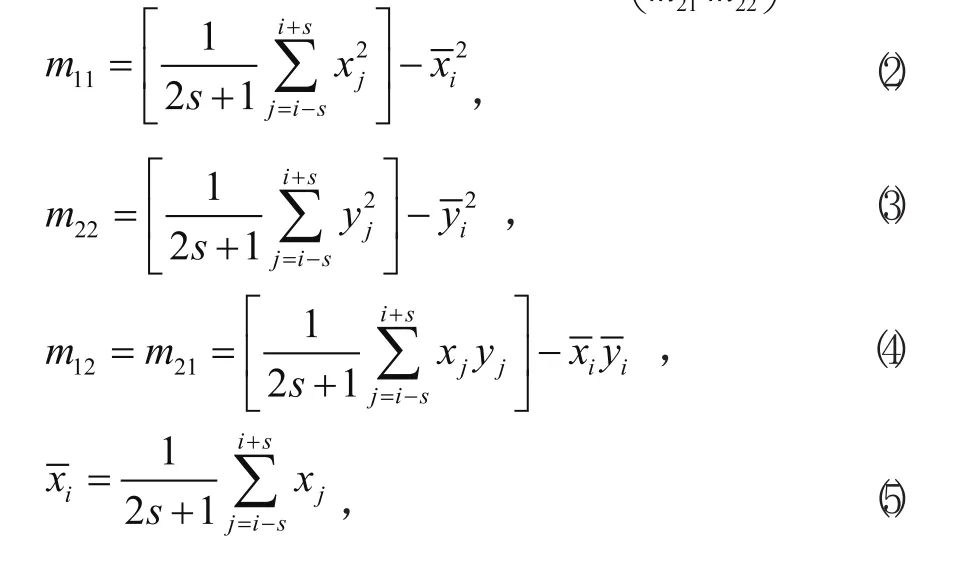
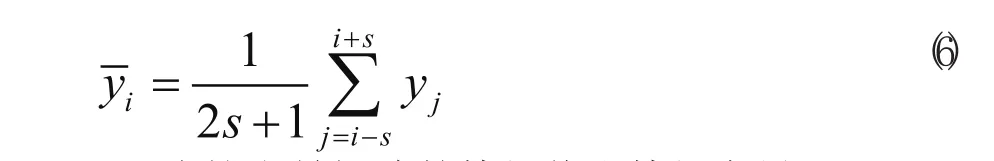
3)求协方差矩阵的特征值和特征向量λ1, λ2,E1,E2,其中λ1是较大的特征值,E1是λ1对应的特征向量。



5)函数θi在尺度k下的小波变换定义为
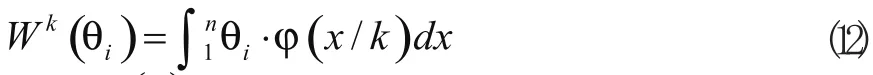
6)在4个不同尺度k下计算方向角θi的小波变换;
8)根据小波变换的取值,如果在曲线的第i个点处θi在四个尺度下的小波变换值都为局部最大值,并且,那么认为曲线的第i个点对应着一个角点[6],标记PFi=1,否则标记PFi=0 。
2 实验

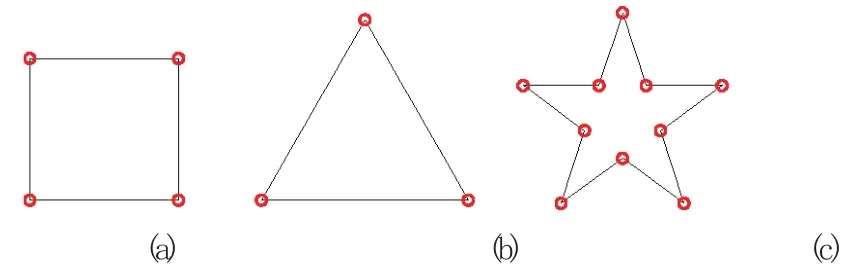
图1 不同形状的曲线链角点检测结果
2)不同夹角的角点在haar小波变换下的响应如表1所示:

表1 不同角度下的小波变换响应
由表1可以得出,对于不同夹角的角点,其根据协方差矩阵得到的方向角函数,在各阶小波变换下均能得到局部极值,可以用于角点的检测及准确定位。
3 结论
由实验可以得出结论,基于协方差矩阵特征向量的小波变换角点检测算法在一致性、准确性和复杂性上都有较好的表现,同时,具有旋转和缩放不变的优良特性。
[1] 陈乐,吕文阁,丁少华.角点检测技术研究进展[J].自动化技术与应用.2005,24(5):1-4.
[2] Liu Wen-Yu,Li Hua,Zhu Guang-Xi.A fast algorithm for corner detection using the morphologic skeleton[J].Pattern Recognition Letters.2001(22),891-900.
[3] Rosenfeld A.,Kitchen L.Gray level corner detection[J].Pattern Recognition Letters.1982(3):95-102.
[4] Fei Shen,Han Wang.Corner detection based on modified Hough transform[J].Pattern Recognition Letters.2002(23):1039-1049.
[5] Moravec H.P.Towards Automatic Visual Obstacle Avoidance[C].In:IEEE International Conference on Robotics and Automation.1997:584-596.
[6] Chi Hao Yeh.Wavelet-Based Corner Detection Using Eigenvectors of Covariance Matrices[J].Pattern Recognition Letters.2003(24):2797-2806.
[7] Azhar Quddus,Moncef Gabbouj.Wavelet-based corner detection technique using optimal scale[J],Pattern Recognition Letters.2002(23):215-220.
TP391.41
A
1009-0134(2010)11(下)-0021-02
10.3969/j.issn.1009-0134.2010.11(下).08
2010-08-07
西南科技大学青年预研基金(07zx3101)
黄华川(1976 -),男,研究方向为计算机视觉与图象处理。
