斜坡地基高填方路堤模型试验极限承载力数值分析*

赵炼恒 王志斌 李 亮 但汉成 刘 项

(中南大学土木建筑学院1) 长沙 410075) (湖南科技大学土木工程学院2) 湘潭 411201)

在山区修建高等级公路,不可避免会遇到大量斜坡地基上的高填方路堤[1-2].但由于其影响因素多、试验经费高等原因,现有试验研究主要集中在小尺寸模型试验、土工离心试验和数值模拟方面,国内采用室内大尺寸模型试验研究的资料较少[3-4].通常大型室内模型的制作和系统测试需花费大量经费和时间,因而结合数值模拟的辅助方式,研究不同工况下斜坡地基上填方路堤物理力学响应与变形破坏形式非常有意义[5-6].本文在室内大型模型试验的基础上,建立了考虑试验模型槽和斜坡地基边界效应的数值计算模型,分析了室内模型斜坡地基上填方路堤变形和破坏的物理力学形态.

1 室内模型试验

1.1 室内试验模型原型

试验依托工程为湖南省常(德)-吉(首)高速公路有代表性的路段,试验模型与原型按照1∶20的比例制作,室内模型试验尺寸如图1所示.

图1 室内模型试验示意图

基本模型试验步骤为:土工试验→模型制作→传感器设置→加载装置设置→加载控制→数据观测→模型开挖观测.

1.2 试验模型槽

试验模型在长方体形状的地下模型槽内修筑完成,模型槽最大尺寸为6 m×3 m×3 m,最大容量54 m3.在槽内修筑钢筋砼刚性挡土墙并在挡土墙上设置观测窗口,以利于对填方路堤变形和破坏的物理形态进行直观观察.试验模型有效尺寸为5.6 m×1.6 m×3.0 m,斜坡地基采用亚砂土水泥改性土模拟,填方路堤采用红砂岩破碎后的碎石土修筑(压实度达到90%),修筑完成的试验槽如图2所示.

图2 试验模型槽

1.3 试验设备

模型试验所需仪器设备包括荷载装置与测试设备两类.利用模型槽两侧的两排预埋锚索并结合横跨于模型槽上方的槽钢作为反力装置,采用1 000 kN卧式液压千斤顶对填方路堤的预制刚性钢筋混凝土板进行加载.根据试验设计目的,模型试验过程中有如下详细测试项目:荷载作用下路堤内部应力、填方路堤变形、极限承载力大小以及滑动破坏面形态与位置.

1.4 模型试验

限于篇幅与本文主题,以下主要阐述模型试验极限荷载下填方路堤破坏形态的试验结果,详细量测过程和试验成果见文献[2].

试验模型在坡顶加载过程中,当外荷载增加到一定量值后,路堤坡面出现均裂隙.继续施加2～3级荷载,通过对加载状态下填方路堤坡面裂隙的发展情况进行观测,发现本次模型试验出现了两种基本的破坏形态:半填半挖路基的折线形破坏形态和高填方路堤的沿斜坡坡面滑动破坏形态.

试验中,认为当坡面出现较大裂隙或路堤变形严重时路堤破坏,此时所加荷载即为该模型的极限荷载.依据该假定,选择其中极具代表性的3个模型试验破坏形式和极限承载力如表1所列.

表1 模型试验滑动面位置及极限承载力

2 数值模型介绍

本文FLAC3D模型计算模型试验极限承载力的基本过程是:编制FISH子程序,采用增量加载直至模型破坏.控制指标为:当模型体出现过度变形或不能再进行稳定的数值计算时,确定模型为破坏,填方路基上施加的荷载即为极限荷载.

2.1 数值计算模型

数值计算中采用能够较为全面的反映影响模型计算的主要因素且建模过程较为简单易行的数值计算模型即可.依据该原则并考虑对称性,数值计算模型取为实际试验模型的一半,并根据试验实际情况设置了3种材料属性,并在各材料接触的地方设置接触面.

根据计算模型对称性,模型中左侧边界只采用x向约束,中右侧、后侧、前侧及底侧边界均采用三向约束,顶面与路堤坡面为自由面.同时为了适应边坡在加载至破坏过程中出现的大位移反应,采用大变形模式进行模拟.典型计算模型如图3.

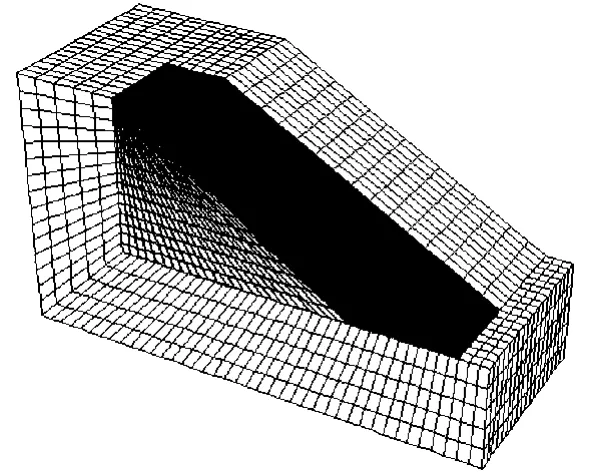
图3 典型计算模型简图

2.2 数值计算材料参数

数值计算分析的准确性取决于本构模型选取的正确性和岩土体力学参数取值的可靠性.本文中斜坡地基和填方材料采用莫尔-库仑模型、模型槽材料采用弹性模型.模型试验中三者之间的接触面特性及材料的基本物理力学性质通过室内常规实验并参考相关资料[7-9]获得,选取参数如表2、表3所列.

表2 数值计算接触面参数

表3 模型试验材料数值计算参数

3 数值计算结果

图4 数值模型3变形破坏图

数值计算过程中增量加载直至模型破坏,当模型体出现过度变形或不能再进行稳定的数值计算时,确定模型破坏.通过数值模型体在荷载作用下的物理力学响应可以较为直观的找出模型体的变形和破坏模式,3个模型体在极限承载力作用下的位移矢量图和位移变形云图如图4所示.

由图4可看出,斜坡地基上半填半挖路基和填方路基呈现出两种不同的破坏模式,半填半挖路基所显示的破坏面均为折线型,而填方路基的破坏面则为斜坡地基坡面与填方路堤的接触面,这与室内模型试验的结果一致.同时由图示路堤位移矢量图及变形云图可以较为清晰地找出滑动面,荷载作用下坡顶土体以向下运动为主,至滑动破坏面则逐渐转化为向坡外临空面运动.量测出模型1、模型2折线形滑动面距路堤顶面分别约为38 cm和45 cm,滑动面出露位置大致位于路堤填土高度的2/3处,与试验误差值在12.5%以内,能够较为准确的印证室内模型试验结果.由模型3的位移矢量图可以看出,填方土体均不同程度的向临空面滑移,且滑移方向基本一致,由此可以确定其滑动面为斜坡地基坡面与填方路堤的接触面,与室内模型试验结果较为吻合.

4 模型试验与数值计算对比分析

数值计算中增量加载直至模型破坏,当模型体出现过度变形或不能再进行稳定的数值计算时,此时在路基上施加的荷载即为极限荷载,极限荷载和破坏面位置与室内模型试验的对比如表4所列.

表4 试验与数值计算滑动面位置及极限承载力对比

数值计算过程中记录的填方土体顶面荷载和顶面竖向位移之间的p-δ关系与室内模型试验的结果对比如图6所示.

由图6和表4可以看出:极限承载力数值计算结果均略大于室内模型试验结果,有两个模型的计算结果误差控制在10%以内,总平均误差约为12.23%;数值模型滑动面则与室内模型试验基本一致.说明数值计算较为准确的反映了室内模型试验的真实物理过程.

图6 顶面p-s曲线

由图5还可看出,数值计算记录的 p-δ关系曲线在加载前期,载荷-位移响应具有较为明显的线弹性性质,这与室内模型试验的 p-δ关系曲线有较大差异.其原因在于:影响室内模型试验结果的因素很多,而数值计算模型是对室内实际模型条件的理想简化,土工试验参数、模型槽与斜坡及填土界面计算参数的选取、室内模型试验所用填土材料的各向异性和不均匀性、反力装置和加载设备的不稳定影响、测量和观测设备的误差以及模型试验过程中存在各种主客观误差均是造成数值计算值与室内模型试验值有误差的原因.

5 结 论

1)基于3个大型室内模型试验结果,通过FLAC3D软件建立数值模型的方法对斜坡地基高填方路堤在极限承载力作用下的力学行为进行了数值模拟.研究表明通过对数值计算模型的校验后再进行室内模型的数值模拟,是实用有效的研究方法,能为充分认识斜坡地基上高填方路堤力学状态提供有益参考.

2)数值模型的计算结果在斜坡地基上填方路堤顶部所能承受的极限承载力、填方土体变形和破坏的物理形态方面,与大型室内模型试验结果吻合较好,说明所采用的数值模型基本正确,较好地反映了真实的室内模型试验过程.

3)数值计算模型是对室内实际模型条件的理想简化,由于多种原因虽不能做到结果与室内模型完全相同,但依然能够定量的反映真实物理过程.通过后续的建模及参数校正后,可进行各种参数的敏感性分析,因而能为设计计算提供参考和依据.

[1]邓卫东.高填路堤稳定性研究[D].西安:长安大学公路学院,2003.

[2]王志斌.岩质斜坡地基上填方路堤稳定性研究[D].长沙,中南大学土木建筑学院,2007.

[3]李碧雄,张利民,陈谦应.斜坡上高路堤的稳定及变形试验研究[J].成都科技大学学报,1996(5):12-18.

[4]赵炼恒,罗 强,杨 峰,等.临坡条形基础极限承载力上限计算[J].武汉理工大学学报:交通科学与工程版,2010,34(1):84-87,92.

[5]高文华,Richard J.Bathurst.条形荷载下加筋土边坡破坏机制的数值模拟[J].土木工程学报,2007,40(6):54-58.

[6]Itasca Consulting Group.Inc.FLAC3D(Fast Lagrangian Analysis of Continua in 3 Dimensions)User manual Version 2.1[M].USA:Itasca Consulting Group,Inc.,2003.

[7]岩土工程手册编写委员会.岩土工程手册[M].北京:中国建筑工业出版社,1994.

[8]水利水电规划设计总院.混凝土面板堆石坝研究成果汇编[M].北京:水利水电规划设计总院出版,1991.

[9]殷中泽,许国华.土与混凝土接触面剪切特性[C]//第六届全国土力学及基础工程学术会议论文集.上海:同济大学出版社,1991:97-100.