海上风机桩式基础结构形式综合模糊优选

翟钢军，李玉刚，康海贵

(大连理工大学建设工程学部，辽宁大连 116024)

利用式(7)、(8)计算非结构性因素的相对隶属度，具体结果见表2和表3。

1 前言

受化石能源资源日趋枯竭、能源供应安全和环境压力等的驱动，近年来世界开始重视利用丰富的海上风能资源，欧盟最早在北海和波罗地海浅海区域兴建了大规模的风电场，其中桩式结构是最常见的风机基础结构［1］。海上风机与陆地结构相比它所处的海洋环境十分复杂和恶劣，是高风险高投入的工程项目，如何降低海上风电成本是当前乃至今后海上风电发展的主要目标，其中基础结构被公认为造成海上风电成本较高的主要因素之一，对基础结构进行优化设计十分必要。海上风机基础的优化设计，首先应是结构形式的优选，在一定的海洋环境、海底地质状况及施工条件下，必定存在一些相对适用的结构形式。

海上风电场基础结构形式方案的优选涉及的指标和考虑的因素很多，其中有些因素是确定性的，而有些因素往往带有模糊性的特点。传统的海洋工程基础结构选型中，决策者多以非此即彼的思想对结构选型进行决策，选出相对适宜的基础结构形式。但是采用传统的方法将很难在方案优选过程中进行各个因素的定量化分析，对方案进行优选是不完善的［2］。文章将影响基础结构选型的模糊因素，根据模糊数学的隶属度理论［3，4］，利用非结构性和结构性决策模糊集分析单元系统理论进行量化，应用多目标单元系统模糊优选模型，对基础结构形式方案进行模糊综合评价和优选。

2 多目标单元系统模糊优选模型

多目标单元系统模糊优选的基本原理是利用与评价对象有关的单因素评判结果构成新的评价矩阵，并利用权重因子作模糊变换，根据各对象的相对隶属度进行优化排序，进而从中选出最优方案。

1)设多目标决策系统由n个方案形成决策集D={d1，d2，…，dn}，由 m 个目标(或因素)组成对决策集D的评价目标集P={p1，p2，…，pm}。则m个目标对n个方案的优劣的评价可以用目标特征值矩阵X(判断矩阵)来表示:

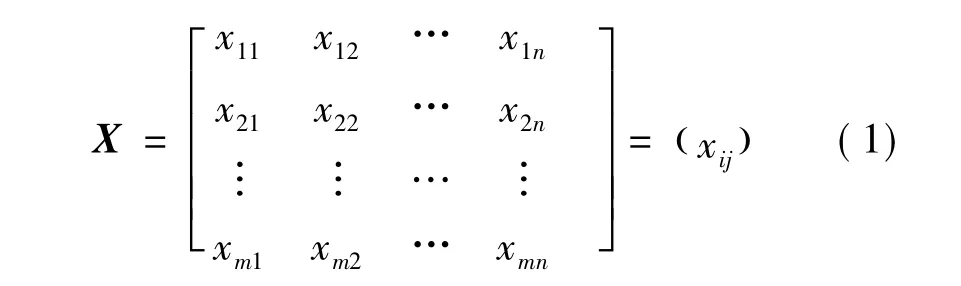
式(1)中，xij为方案 j目标 i的特征值(i=1，2，…，m;j=1，2，…，n)。

2)根据相应的优选模型原则，在目标特征值矩阵X的基础上变化出目标相对隶属度矩阵R:

式(2)中，rij表示第j个方案在第i个目标下的相对隶属度。

3)设多目标系统中m个目标的权重不同，权向量为:

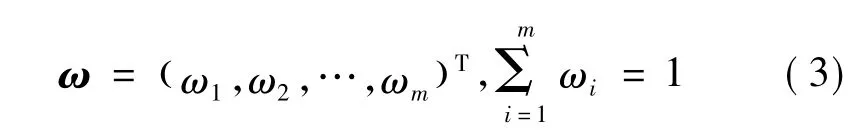
4)设方案j对优等决策的相对隶属度以表示，则多目标单元系统模糊优选模型为:

式(4)中，p为距离参数，p=1时为海明距离，p=2时为欧氏距离。根据以上步骤所求得的目标相对隶属度和目标权重，按照上式计算出所有方案的相对隶属度uj，uj最大的方案即为满意决策。

3 确定因素的相对隶属度及权重

在方案选型评价的模糊优选中，确定各因素对决策集的隶属函数与隶属度是确定模糊关系矩阵的关键。

设m个目标集P={p1，p2，…，pm}中包含有 q个非结构性因素(或定性目标)，即 C={c1，c2，…，cq}(q≤m)。现研究方案集D中的方案dk与dl(就因素ci而言)进行“优越性”的二元比较，得决策集的优越性二元对比矩阵

按照优先关系和排序一致性原则将优越性二元对比iE矩阵的各行相加，得到一个表示i目标下各决策元素的优越性特征值的列向量xij。

非结构性因素(或定性目标)就“优越性”而言为越大越优，则非结构性因素的相对隶属度为:

对于m个目标集 P={p1，p2，…，pm}中除了 q个非结构性因素(或定性目标)外的m－q个结构性因素(或定量目标)，根据计算或估算可以得到其具体或大约的目标特征值xij，但是由于不同的评估目标在数量级上是各不相同，必须将其进行规范化，根据定量目标的性质可按效益型、成本型和适中型目标确定目标的相对优属度:

通常，确定各因素的权重是比较困难的。为了 解决这一问题，采用类似于确定因素相对隶属度的非结构性模糊决策法来确定权重，其基本原理与确定影响因素隶属度一致。目标集P中的元素pk与pl就“重要性”作二元比较，得到目标集中各因素对“重要性”的二元对比矩阵β，作归一化处理得目标i的权重 ωi。

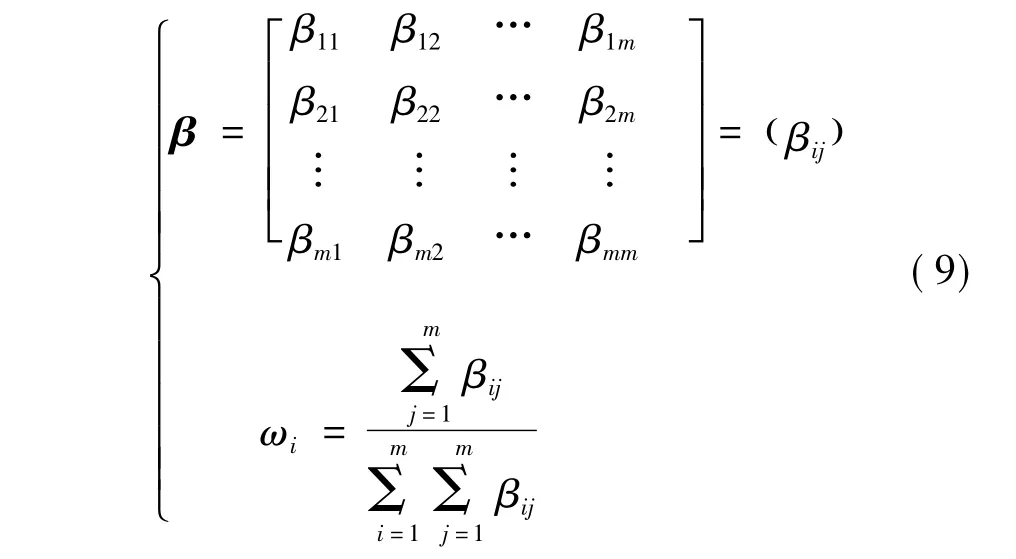
式(9)中，βij仅在 0，0．5，1．0 中取值。

4 工程实例描述

某海上风电场，水深在5～15 m，海床面以下30～50 m深度内地基土以砂质粉土及粉质黏土为主，海流平均流速3．45 m/s，平均波高 2．25 m，波周期 6．8 s，波速 9．0 m/s，选定的风力发电机组为3 MW，风机荷载资料由厂家提供(见表1)。根据区域环境条件和场地的工程地质条件，并参考欧洲国家现有海上风机基础结构形式、国内外海上石油平台、海上灯塔的设计经验，提出4种基础形式进行结构方案设计:单根钢管桩基础，三脚架组合式钢管桩基础，四脚架组合式钢管桩基础，高桩承台群桩基础。

表1 风力发电机组荷载汇总表Table 1 Summary of w ind turbine loads

以上4种风机基础结构形式方案组成本文考虑的方案集，即 D={d1，d2，…，dn}={单桩(方案 1)，三桩(方案2)，四桩(方案3)，高桩承台(方案4)}，其立体视图如图1所示。

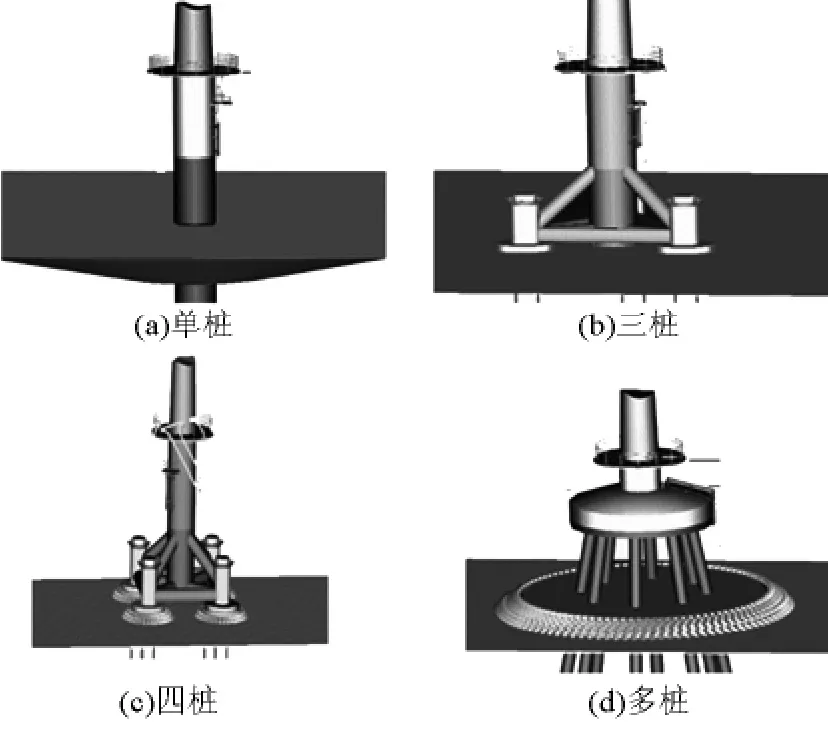
图1 4种风机基础形式设计方案的立体视图Fig．1 Three dimensional view of 4 kinds of fan base design

5 基于非结构性因素的基础结构形式的模糊优选

5．1 非结构性因素的选取

从结构功能、经济性能、施工可行性等方面考虑，影响基础结构选型的因素很多，包括非结构性因素，如“结构对环境的影响程度”等和结构性因素，如“施工费用”等，在此建立4种方案所对应的优选半结构性因素集:P={p1，p2，…，pm}={技术难度，抗冲力荷载能力，环境影响，施工工期，检修维护难易，施工难度，施工费用，制造成本，维护费用}。同时为了避免因因素较多导致某些因素权数较小，出现大量“淹没”情况，对此模型根据各因素的影响程度进行分类。因素 p1，p2，p3，p4，p5这 5 个因素的影响程度较小，将其作为一层进行一级模糊优选。因素p6，p7，p8，p9这4个因素对结构形式选型的影响程度大，作为第二层进行二级模糊优选［5，6］。在计算中，考虑各层之间的相关性即耦合作用，将一级模糊优选的结果代入二级模糊优选，既使次要因素的权数有效降低，又能突出主要因素的影响，分析过程如下:

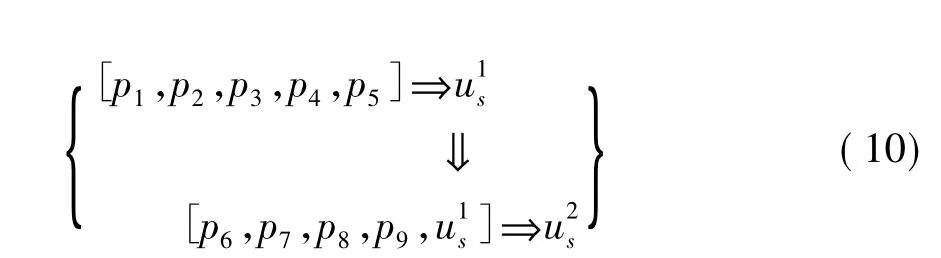
5．2 非结构性因素的相对隶属度的确定

利用式(7)、(8)计算非结构性因素的相对隶属度，具体结果见表2和表3。

5．3 确定目标的权重

利用式(9)计算因素的权重，具体结果见表2和表3。

5．4 选型优化结果

有了模糊目标集和权重集后，应用多目标单元系统模糊优选模型即式(9)，取海明距离p=1时，得决策相对隶属度向量u1，取欧式距离p=2时，得决策相对隶属度向量为u2，结果见表2和表3。

表2 一级模糊优选结果Table 2 First－step fuzzy optim ization results

表3 二级模糊优选结果Table 3 Second－step fuzzy optim ization results

5．5 优选结果分析

从模糊优选结果可以看出，方案2(u2=0．993 8)、方案 3(u2=0．968 3)明显优于其他设计方案，其中方案2优于方案3。需要强调的是，在以上计算中，因素的层次划分及因素权重的确定是在确定海上风力发电场基础结构形式方案时采用的，随着工程进入施工期、运营期，层次的划分及权重也将随之改变，因为在开发初期投资是最重要的，但随着进入施工期、运营期其因素的重要性也将发生改变。但不管处于何种时期，应用此方法都可得到比较理想的优选结果。

6 基于结构性因素的基础结构形式的模糊优选

6．1 确定基础结构模糊选型优化的结构性因素

基础结构的选型优化是一个涉及多层次、多因素的复杂规划问题，在结构性因素中如果仅考虑重量目标是片面的。下面根据基础的实际情况引入强度可靠度、结构刚度以及结构抗震性能总共4个目标，对上述4种方案的基础形式进行模糊多目标选型优化。

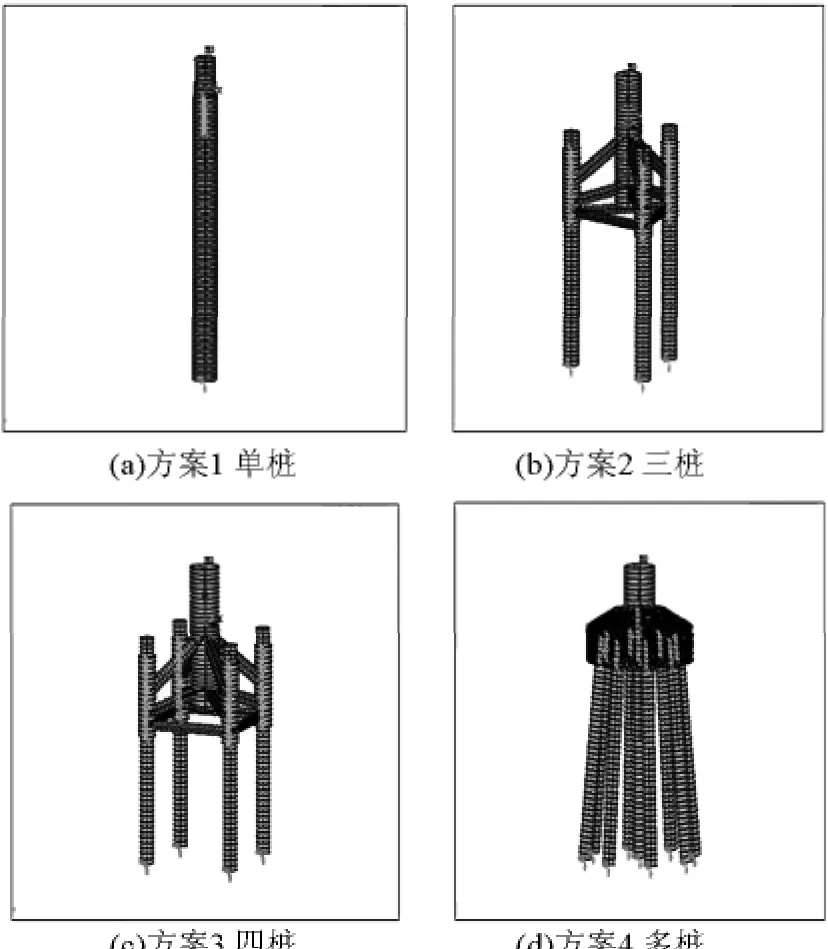
图2 ANSYS模型Fig．2 ANSYSmodel

1)重量计算。在优化设计中得到的基础结构重量，是以6倍桩径考虑的，基础结构有限元分析模型如图2所示，利用文献［7］粒子群优化模型，对方案1、方案2、方案3、方案4四种结构形式进行统一的优化设计，从而得到在相同条件下结构性因素的相关数据。最后，以此为依据进行模糊选型优化，其中，方案4中承台为钢筋混凝土承台，将钢筋混凝土承台按照钢筋混凝土1 500元/m3与Q345型钢板10 000元/t折合成用钢量。以上工作作为初步设计的一部分，由于分析过程中，没有考虑桩与土之间的相互作用即土壤的非线性影响，并且采用简化计算模型，因此其优化设计结果将作为后续工作的初步设计尺寸或参考尺寸。

2)刚度计算。刚度在模糊优选中是一个重要指标，此次选型优化计算中刚度指标的选取是在正常工作条件下(而不是单位载荷作用下)基础法兰面处节点水平位移值δ，其值见表4。

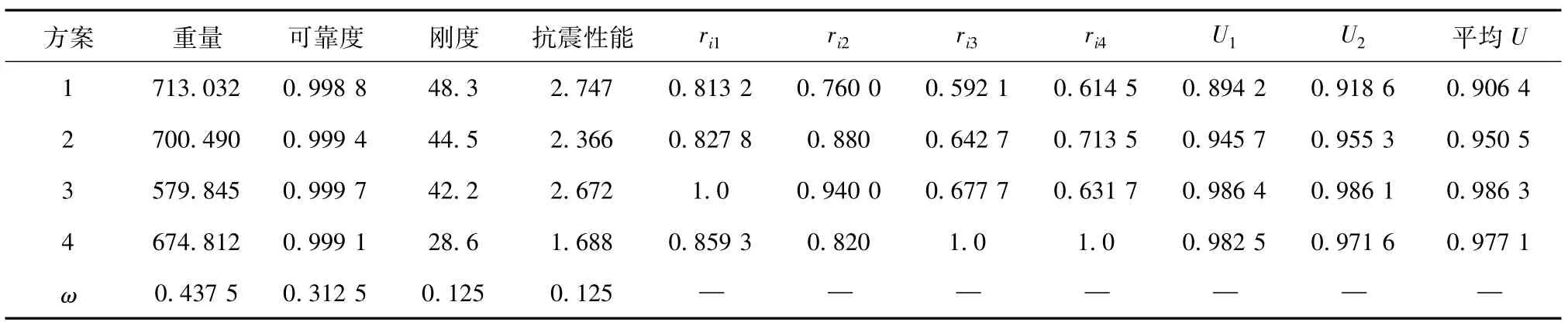
表4 选型优化结果Table 4 Lectotype optim ization results

3)结构抗震性能。在高耸结构中，地震是主要荷载形式之一，水平作用是主要的，但还需要考虑竖向作用。在有限元分析中，地震荷载以加速度的形式作用于结构，随时间而变化，采用ANSYS软件中的瞬态分析来模拟计算地震对基础结构的作用。分析计算过程中，4种方案采用同一地震加速度数据。计算结果见表4。

4)强度可靠度计算。采用文献［7］推荐的基于支持向量机分类技术的可靠度方法，其计算结果见表4。

6．2 结构性多目标模糊选型优化计算过程、

结果及分析

1)结构性目标模糊化。一般来说，结构性因素之间一般不具有可比性，进行优选时必须将目标函数模糊化。在本模糊选型优化中，按下列方法确定其相对隶属度:

重量:重量目标采用相对越小越优模型公式将重量模糊化求得其相对隶属度，表达式为

式(11)中，ri1为重量的相对优属度;Wmin为4种方案中的最小重量;Wi为第i种方案的重量。计算结果见表4。

可靠度:可靠度目标采用绝对越大越优模型公式，将可靠度目标模糊化求得其相对隶属度，表达式为

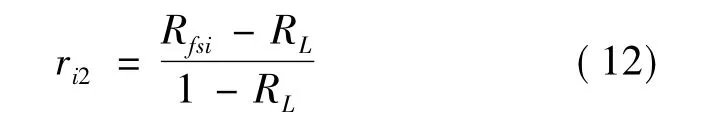
式(12)中，ri2为可靠度的相对优属度，Rfsi为第i种方案的可靠度，RL为工程上允许的可靠度的下限值，为0．995。计算结果见表4。

刚度:刚度目标也采用相对越小越优模型公式

式(13)中，ri3为刚度的相对优属度;δmin为四种方案中的最小刚度;δi为第i种方案的刚度。计算结果见表4。

抗震性能:抗震性能目标也采用相对越小越优模型公式

式(14)中，ri4为刚度的相对优属度;¯ωmin为四种方案中的最小刚度;¯ωi为第i种方案的刚度。计算结果见表4。

2)确定目标权重。确定目标的权重仍然采用模糊优先关系和互补原则，与非结构性因素权重的确定相同，结果如下:重要性排序为重量、可靠度、刚度、抗震性能。

3)确定决策相对隶属度向量u。应用多目标单元系统模糊优选模型，取海明距离p=1时，得决策相对隶属度向量u1，取欧式距离p=2时，得决策相对隶属度向量为u2，结果见表4。

从表4可看出，关于上述指标的模糊优选，不管取海明距离p=1还是欧式距离p=2，四桩结构形式都是最优的。同时可以看出，关于上述指标的模糊优选，各方案的优选结果相差不大，结构的可靠度指标、刚度指标及抗震性能指标对结构的选型优化有一定的影响，但主要还是取决于用钢量的多少。

7 基于综合系统的基础结构形式的模糊优选

设整个系统分解为H层，最高层为H。若最低层(第1层)有若干个并列的单元系统，每个单元系统均有多个目标特征值输入，根据多目标单元系统模糊优选模型对每个单元系统计算输出──方案相对优属度向量:

它组成第2层中某个单元系统的第i个输入，如图3所示。

图3 3层模糊优选系统图Fig．3 3 － layer fuzzy optim ization system

设第2层并列单元系统的权向量为ωj=(ω1j，ω2j，…，ωmj) ，且则多目标单元系统模糊优选模型可用于第2层中单元系统的计算。如此从第1层向第H层进行计算，直至最高层。由于最高层中只有一个单元系统，可得最高层单元系统的输出──方案的相对优属度向量。

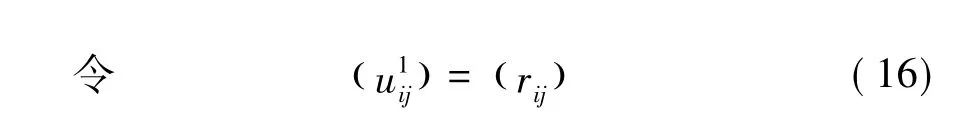
据此可优选多层次多目标系统满意方案，现将所考虑的系统分解为非结构性因素子系统、结构性因素子系统。各子系统的输入指标作为系统的输入层，具体包含前几节中所述的因素。系统模型结构如图4所示。

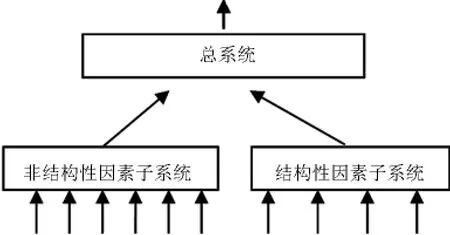
图4 基础结构系统模型结构图Fig．4 Infrastructure system model structure diagram

根据以上所述以及前几节的计算，可得第2层的选型优化结果(见表5)。

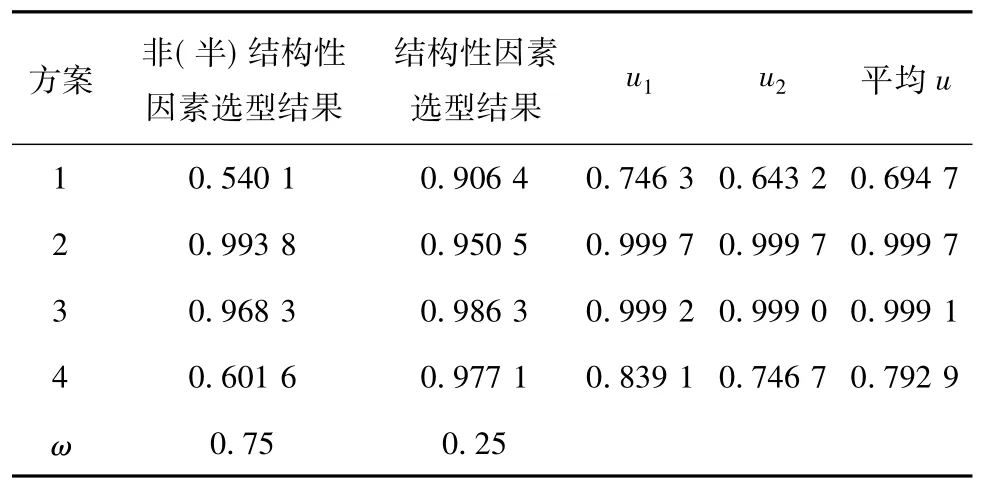
表5 选型优化结果Table 5 Lectotype optim ization results

从表5可看出，不管取海明距离p=1还是欧式距离p=2，模糊优选结果为三桩结构形式稍稍优于四桩结构形式，明显优于单桩及多桩结构形式。因此，在后续工作中应将重点放于三桩和四桩结构形式上。

8 结语

利用模糊数学理论解决了海上风机桩基基础选型的问题，通过分析得到以下结论:

影响基础结构选型优化的因素多为非结构性因素，在确定其相对隶属度时受主观因素的影响较大，用非结构性模糊决策集分析单元系统理论确定其相对隶属度和权重，可以有效地降低确定相对隶属度和权重的人为影响。

将因素分层综合考虑了影响结构选型的各种非结构性和结构性因素，通过计算可知，用此优选模型进行基础结构选型优化可得到比较理想的优选结果。

在确定性的海洋环境条件下，考虑多种不确定性影响因素，通过对海上风电场4种基础结构形式的模糊优选研究，可以给出确定性的结论:三桩结构与四桩结构形式明显优于单桩及多桩结构形式。

［1］ Simon－Philippe Breton．Geir Moe，Status，plans and technologies for offshore wind turbines in Europe and North America［J］．Renewable Energy，2009，34(3):646 －654．

［2］ 翟刚军．海洋固定平台模糊优化与模糊可靠性研究［D］．大连:大连理工大学，2001．

［3］ 陈守煜．工程模糊集理论与应用［M］．北京:国防工业出版社，1998．

［4］ Zadeh L A．Fuzzy sets as a basis for a theory of possibility［J］．Fuzzy Sets and System，1999，100:9 －34．

［5］ 翟钢军，封 盛，康海贵，等．海洋平台设计选型的多级模糊优化及非结构性模糊决策分析［J］．中国造船，2002，43(1):23－29．

［6］ 康海贵，翟钢军，李玉成．多级工程模糊优选在海上平台设计选型中应用［J］．大连理工大学学报，2001，41(3):368 －371．

［7］ 李玉刚．桩式海上风机基础可靠度分析及优化方法研究［D］．大连:大连理工大学，2009．