引风机内颗粒沉积的数值模拟

2010-03-28田松峰

电力建设 2010年12期

田松峰，李滢，周玉

（电站设备状态检测与控制教育部重点实验室（华北电力大学），河北省保定市，071003）

0 引言

火力发电厂中，引风机将燃料燃烧后形成的烟气从锅炉中连续不断地吸出，并经由烟道排入大气[1]。引风机虽然设置在除尘器之后，但是由于除尘器并不能将烟气中的全部固体微粒去除，剩余的固体微粒随烟气一起进入引风机，特别是当除尘器不能正常工作时，大量的飞灰颗粒将随烟气进入引风机，造成引风机剧烈磨损[2]。

计算流体力学（computation fluid dynanics，CFD）可以将流体力学实验研究与理论分析联系起来，用数值模拟的方法研究流体运动的物理特性。本文采用CFD方法研究离心式通风机内部的气固两相流动，对风机降低磨损和提高安全性有一定的现实意义。

1 引风机模型

1.1 引风机结构

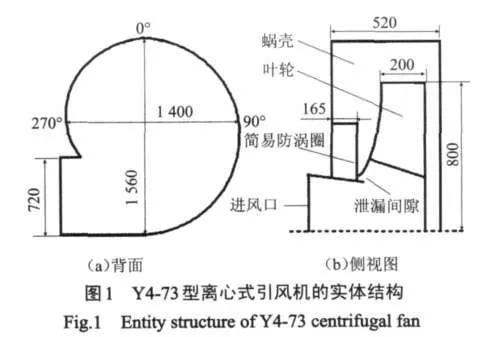
Y4-73型离心式引风机的叶轮由12片叶片构成，与后倾机翼斜切的叶片焊接于锥弧形的前盘与平板形的后盘中间。收敛、流线形的进风口制成整体结构，用螺栓固定在风机入口侧。用来调节风机流量的装置，轴向安装在进风口前面。引风机的结构如图1所示，图中长度单位为mm。

1.2 建立模型

应用Fluent软件的前处理模块Gambit，建立引风机的空气动力学模型。叶片采用简化的翼型叶片，以保证得到质量较好的网格。建立起引风机的几何模型后，分别对蜗壳曲线、叶轮出口圆、各个叶片、叶轮进口圆建立面，之后采用布尔分割法将风机分成蜗壳区域和叶轮区域[3]。

1.3 网格划分

由于叶轮和蜗壳的结构和流动复杂性不同，则网格的尺寸也不同，在划分网格时，可分别划分叶轮和蜗壳的网格。对于叶轮区域，由于受到强烈旋转作用，其流场情况复杂，同时叶片结构也较复杂，存在小尺寸结构。因此，该区域的网格尺寸要尽可能小。但是，受计算机性能限制和可能出现负网格的影响，网格尺寸也不能太小。综合考虑，叶轮区域选择间距为0.8 mm的三角形结构化网格。对于蜗壳区域，其结构相对于叶轮简单一些，但流动比较复杂且受到叶轮旋转的影响，所以采用间距为1 mm的三角形结构化网格。引风机网格划分如图2所示。

2 气固两相流数值模拟

2.1 基本方程

重整化群k-ε模型将重整化群的数学方法应用于瞬时Navier-Stokes方程，该模型中的常数与标准k-ε模型不同，且方程中出现了新的函数或项[4]。重整化群k-ε模型可应用于不同类型的流动模拟，包括旋转均匀剪切流、包含射流和混合流的自由流动、管道内流动、边界层流动以及带有分离的流动。本文采用重整化群k-ε模型，对Y4-73型离心式引风机进行流场的数值模拟。

2.2 边界条件设置

在Gambit中设置求解器为Fluent 5/6，采用Simple算法对引风机内流场进行非定常流动的数值模拟。根据不可压缩流的特点，定义速度进口和流量出口。壁面函数选取无滑移标准壁面函数。

引风机进口处的速度边界条件为匀速，其值为3.7 m/s。叶片选择移动壁面，叶轮出口为interface，蜗壳出口选择流量边界条件，叶轮内的流体选择Moving Reference Frame，其他边界设为默认的壁面边界[5-6]。

2.3 结果分析

Y4-73型离心式引风机的非定常流速度矢量如图3所示。当气流流经旋转叶片时，产生垂直叶片表面的相对速度，由于叶轮叶片不断做功，气体速度沿流动方向不断升高，气流以较高的流速流入蜗壳，沿蜗壳通道逐渐减小[7]。

待非定常流动收敛后，加入颗粒，采用离散相模型和拉格朗日颗粒轨道模型进行数值模拟，并进行如下假设：（1）流体在流动过程中不可压缩；（2）固体颗粒是具有相同直径、密度均匀的球体；（3）当固体粒子所占体积比例小于0.5%时，认为粒子的存在对气流参数的影响很小；（4）忽略粒子间的相互作用；（5）粒子在气流中受到的作用力主要是气体的黏滞阻力，其他力忽略不计；（6）气固两相具有相同的温度场；（7）不考虑固相与壁面的摩擦力[8]。引风机中颗粒的边界条件如表1所示，表1中颗粒类型为惯性颗粒。

表1 颗粒边界条件及参数设置Tab.1 Boundary conditions and parameters of grain

表1中初始坐标和速度的设定值表示颗粒随气相运动。进行颗粒数值模拟时，首先根据模拟时间选择合适的启停时间，再进行初始化和迭代计算。数值模拟得到的颗粒分布状态如图4所示。

图4中，颗粒主要在叶片的非工作面上沉积，固体颗粒从风机入口进入叶轮通道，首先有一小部分颗粒与叶片前缘相撞后发生反弹，而其余部分与吸力面碰撞后进入叶轮通道，被气流裹挟甩出叶轮。颗粒在黏性力和离心力的共同作用下，前进一段距离后再次与叶片发生碰撞，而这次碰撞发生在叶片压力面的后缘区域[9-10]。在这2个区域中与叶片发生碰撞的颗粒，若具有一定粘性且在流动边界层内，就会在叶片表面沉积。而一旦有灰粒沉积就会引起叶片磨损，进而导致风机震动噪声过大，严重影响风机工作效率和性能[8]。

3 气力吹灰

清除风机叶轮上的积灰，常用的方法有水力吹灰和气力吹灰。水力吹灰过程中存在沿程损失和局部阻力损失，为了满足对喷水速度的要求，必须提高喷水压力，因此需增大提升水压所需的能量，同时增加了喷水量，使得风机壳上的排水孔无法满足及时排水的要求，从而出现风机叶轮浸泡于水中的现象，使喷水清灰失去意义。本文采用气力吹灰方式来消除引风机叶轮上的积灰。

在引风机内加入速度较高的气流，通过数值模拟验证其对颗粒吹扫的能力，计算结果如图5所示。初期颗粒随气流发生90°偏转进入叶轮通道。受风机内旋转流场的影响，固体颗粒与叶片非工作面发生碰撞，且主要沉积于叶片前缘和后缘部位。

以清除叶片入口处积灰为例，计算清灰气流应具有的速度。叶轮入口的圆周速度为

式中：D1为叶片进口直径，m；n为风机转速，r/min。对于Y4-73型离散引风机，D1=1 m，n=1 450 r/min，由式（1）得u=75.8 m/s。

引风机入口速度分布如图6所示。图中：w为相对速度；v为绝对速度。由图6中的入口速度三角形可知，要使射流作用于积灰处，w和u之间的夹角α应大于叶片入口安装角，取叶片入口安装角为45°。当v和u之间的夹角大于90°时，w指向叶片的工作面，射流介质不能对叶片非工作面上的积灰产生直接的作用力，除灰效果不理想；当其夹角等于90°时，除灰效果最好。因此，最佳射流方向为径向射流[11]，此时，α= 45º，有

由式（2）得v=75.8 m/s，当射流速度大于75.8 m/s时，清灰气流才能作用于积灰处。考虑到负压和阻力的影响，取喷嘴气流速度为90 m/s，为了同时保证吹扫效果和防止振动，在对称位置加装喷嘴。加装喷嘴后，颗粒分布如图7所示。

由图7可看出：由于高速吹扫气流的加入，提高了颗粒速度并减少了由于叶轮旋转对颗粒运动轨迹的影响；在叶片前缘部分，使颗粒的速度方向偏向叶轮通道，减少与前缘的碰撞；在后缘部位，由于颗粒在进入蜗壳之前仍有较高的速度，从而减少与叶尾部分的碰撞。因此，加入吹扫气流可减少颗粒与叶片的摩擦，降低沉积概率[10-12]。