四运放多功能KHN滤波器的设计
2010-03-26孔令云袁战军王向阳
李 安,孔令云,郭 静,袁战军,王向阳,商 莹
(陕西国际商贸学院 电子与信息工程系,陕西 咸阳 712000)
通用二阶滤波器有两种形式,一种是TT(Tow-Thomas)滤波器,另一种是KHN(Kerwin-Huelsman-Newcomb)滤波器。与TT滤波器相比,KHN滤波器不仅能直接实现低通和带通 滤波,还能实现高通滤波,应用广泛,是现代电流模式滤波器设计的基础[1-6]。然而KHN滤波器属于单输入、三输出的通用滤波器,不能实现三输入、单输出通用滤波。由于电阻比有限,因此其Q值不能太高[7]。三个集成运放中,有一个运放的反相端不满足虚地,则对运放提出较高要求。
鉴于KHN滤波器在现代电流模式电路中的地位,提出了另一种形式的KHN滤波器,它不仅能实现单输入、三输出的通用滤波,也能实现三输入、单输出通用滤波,电路的极点频率和品质因数能够被独立、精确的调节,电路也能被修饰成一个正交振荡器。电路包含4个通用集成运放、2个电容和11个电阻,且所有运放的反相输入端均虚地。
1 电路原理
图1给出了由四运放构成的多功能电压模式二阶电路,其中有1个大反馈环和2个小反馈环。

图1 四运放多功能二阶电路Fig.1 Multi-functional second order circuit with four OPs
设 R1=R2=R,C1=C2=C,R5=R6,使用 MASON 公式,可得到三环路的增益和为

电路的行列式为
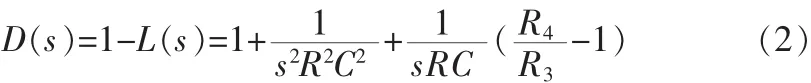
电路的极点频率和品质因数分别为


式(3)表明,通过同步调整 R1、R2,可实现极点频率的独立调节,而不影响品质因数。式(4)表明,通过调整 R4、R3的电阻比,可实现品质因数的独立调节,而不影响极点频率,从而实现二者的正交调节。值得注意的是,通过调整R4/R3,很容易实现高Q电路,特别是当R4=R3,Q=∝,这意味着电路变成了一个正弦振荡器,其频率可由R、C调节。
若 Vo3=Vo, 则从电压源 Vi1、Vi2、Vi3到输出端 Vo的前向通道增益分别为-1/s2R2C2、1/sRC、-1,由 MASON 公式知,相应的传输函数为

由式(5)、式(6)、式(7)可知,若 Vo3是输出,则 Vi1是低通输入,Vi2是带通输入,Vi3是高通输入。图1所示电路是从一个端口输出信号,从3个端口输入信号的双二次节,分别实现了低通、带通和高通二阶滤波。相应的增益常数分别为GL=-1,GB=Q,GH=-1。
如果Vi3=Vi,则从Vi到输出端 Vo3、Vo1的前向通道增益分别为-1和1/sRC,从Vi到输出端 Vo2的前向通道增益和为-1/s2R2C2+1/sRC-R4/sRCR3,相应的传输函数为

若取 R4/R3-1=1,则由式(8)、式(9)可得

由式(8)、式(9)可知,若 Vi3是输入,则 Vo3是高通输出,Vo1是带通输出。式(10)、式(11)说明,Vo2并不是低通输出,当满足条件R4/R3-1=1时,Vo1+Vo2才是低通输出,这是一个值得注意的问题[8-9]。所以图1电路也能从一个端口输入信号,从多个端口输出信号的双二次节,同时实现了高通、带通和低通二阶滤波。相应的增益常数分别为GH=-1,GB=Q,GL=-1。
2 计算机仿真
为了验证电路的正确性,在EWB5.0平台上创建图1电路,其中集成运放选用通用运放μA741,这里仅仿真单输入、三输出滤波器。 取 R1=R2=R=10 kΩ,C1=C2=C=10 nF,R5=R6=10 kΩ,R4=20 kΩ,R3=10 kΩ, 则理论给出 fo=1.5915 kHz,Q=1,GH=-1,GB=1 ,GL=-1。 仿真结果如图 2所示。 用 EWB5.0提供的指针可测得:fo=1.5849 kHz,Q=1.0113,GH=-1,GB=1.0113,GL=-1。

图2 单输入、三输出二阶滤波器的仿真结果Fig.2 Simulation results of filter with one input,three outputs
为了说明电路的品质因数受电阻比R4/R3控制,仍取R1=R2=R3=R5=R6=10 kΩ,C1=C2=10 nF, 使 R4分别为 12.5、15、17.5、20 kΩ 时,理论给出 fo=1.5915 kHz,Q 分别为 4、2、1.33、1。 用 EWB5.0可测得 fo=1.6298 kHz,Q分别为 4.0690、2.0313、1.3503、1.0108,仿真结果如图3所示。
为了说明电路的极点频率受R1、R2控制,且与R4、R3无关,取 R3=R5=R6=10 kΩ,R4=20 kΩ,C1=C2=10nF,使 R1=R2=R,分别为 1、10、100 kΩ 时,理论给出 Q=1,fo为 15.915、1.5915、0.15915 kHz,。带通滤波器的频率特性如图4所示。用EWB5.0 可测得 fo分别为 16.3789、1.6379、0.163789 4 kHz时,相应的Q分别为1.1427、1.0103、0.9995。显然频率较高时,出现了Q增强现象,这是由于运算放大器的有限增益带宽积造成的[7]。
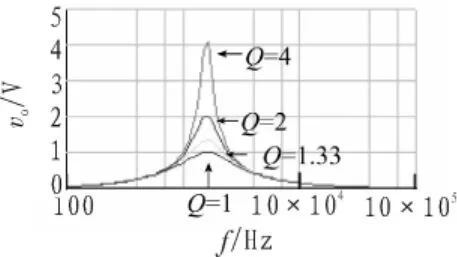
图3 品质因数与R4/R3关系的仿真结果Fig.3 Simulation results for the relationship between quality factor and R4/R3

图4 极点频率与R关系的仿真结果Fig.4 Simulation results for pole frequency and R
理论上,当R4=R3,电路变成了振荡器,仿真结果表明R4要稍小于R3,才能维持振荡。取R1=R2=R3=R5=R6=10 kΩ,C1=C2=10 nF,当 R4=9.9 kΩ〈R3=10 kΩ,电路振荡,由于 Vo2比 Vo1超前90°,所以Vo2和Vo1是两相正交正弦波。理论给出fo=1.5924 kHz。仿真结果如图5所示。实测fo=1.5588 kHz。造成频率下移的原因是运算放大器的有限增益带宽积[10]。造成波形失真的原因是无限幅电路,只要给积分器增加二极管限幅电路[7],即可改善波形。可见计算机仿真结果与理论设计基本一致,说明所设计电路正确有效。

图5 正交正弦振荡器的仿真结果Fig.5 Simulation results for quadrature sinusoidal oscillator
3 结 论
使用4个通用集成运放、2个电容和11个电阻,设计二阶通用滤波器,其参数设置如下:fo=1.5915 kHz,Q=1,GH=-1,GB=1,GL=-1。该电路既可单输入、多输出同时实现低通、带通和高通滤波,也可以多输入、单输出分别实现低通、带通和高通滤波。电路除具有低的灵敏度外,还具有以下特点:1)电路的极点频率和品质因数能独立调节,容易获得高Q滤波;2)所有集成运放的反相输入端虚地,因而承受的共模电压为0,对运放的要求不高;3)电路还可被调节成一个频率可调的正交正弦振荡器。
[1] Keskin A ü,Biolek D,Hancioglu E.Current-mode KHN filter employing current differencing transconductance amplifiers[J].AEU-Int.J.Electron.Commun,2006,60(6):443-446.
[2] Ssahram M,SaitT.New current-mode current-controlled universal filter with single input and three out-puts[J].International Journal of Electronics,2001,88 (3):333-337.
[3] Tangsrirat W,Pukkalanun T.Structural generation of two integrator loop filters using CDTAs and grounded capacitor[J/OL]. International Journal of Circuit Theory and Applications,2009 (37):616[2009-07-10].http://www3.interscience.wiley.com/journal/122507208.
[4] 李永安.用AOA设计有源补偿双二阶电流模式滤波器[J].电讯技术,2008;48(8):92-96.LI Yong-an.Design of biquad current mode filter with active compensation based on AOA [J].Telecommunication Engineering,2008,48(8):92-96.
[5] 李永安.用AOA Deboo积分器设计通用二阶电流模滤波器 [J].电子器件,2007,30(5):1591-1593.LI Yong-an.Designing of universal second-order currentmode filter based on AOA deboo integrator's[J].Chinese Journal of Electron Devices,2007,30(5):1591-1593.
[6] 李永安.基于MO-CDTA的电控调谐多功能电流模式二阶滤波器及振荡器[J].微电子学,2009,39(5):670-672.LI Yong-an.Electronically tunable multifunctional currentmode filter and oscillator using MO-CDTA[J].Microelectronics,2009,39(5):670-672.
[7] Franco S.Design with operational amplifiers and analog integrated circuits [M].3rd.New York:Mc.Graw-Hill Science Engineering,2001:120-130.
[8] 王楚,余道衡.电子线路解题指南[M].北京:北京大学出版社,2005:46-56.
[9] 李永安.适宜集成的KHN滤波器 [J].电讯技术,2007,30(5):71-73.LI Yong-an.Design of KHN filters easy to be integrated[J].Telecommunication Engineering,2007,30(5):71-73.
[10] Budak A.Passive and active network analysis and synthesis[M].Boston:Waveland Press,Prospect Heights,IL,1991:320.
