关节式准柔性后缘翼型的气动特性分析

尹维龙

(1.哈尔滨工业大学复合材料与结构研究所，哈尔滨150080，yinweilongbj@sina.com.cn; 2.哈尔滨工业大学力学博士后流动站，哈尔滨150080)

目前，绝大多数飞行器的副翼和襟翼均通过机械式铰链装置使控制面产生偏转来改变机翼的弯度，进而改变机翼的气动升力.但是，传统控制面偏转时，机翼表面斜率发生突变，易产生气流分离，降低控制面的操纵效率［1］.为此，人们提出了一种柔性后缘可变弯度机翼的概念.柔性后缘机翼采用了柔性蒙皮技术，使得后缘在变形过程中机翼表面始终保持光滑和连续，改善了机翼表面的压力分布，提高了气动效率［2－3］;同时，可变弯度变形机翼在变形过程中机翼表面始终处于无缝状态，大大地减少了雷达回波，从根本上提高了飞行器的隐身性能.早在1920年就出现了可滑动后部大梁的变弯度机翼，但复杂的结构使其一直没有得到实际应用.为此，一些学者采用多关节式偏转后缘的变形方案.Monner［4］提出了一种称为“可转动翼肋”机构概念.马里兰大学的研究人员［5］设计了一种机械式“多节式”可变弯度机翼.杨智春等［6］也验证了“可转动翼肋”5关节式变形后缘的结构方案，并讨论了后缘变形路径对气动特性和驱动力的影响.Icardi［7］设计了一种形状记忆合金扭转驱动器驱动的3关节式准柔性后缘.为了取消了笨重的转轴，Barbarino［8］提出了一种翼段通过柔性铰链来连接的4关节式后缘.本文从翼面压力分布和转轴力矩的角度分析多关节后缘的利与弊.

1 柔性后缘的气动特性

对于传统偏转式后缘而言，后缘偏转量可以直接采用控制面绕铰链转轴偏转的角度来衡量;而对于柔性后缘而言，其变形后的外形是曲线，无法找到固定的旋转参考点，也就无法直接来定义偏转的角度.目前，大多数学者参照文献［9］提出的方法来定义柔性可变后缘弯度机翼的等效后缘偏角(以下简称为后缘偏角)，表达式如下:

其中:hT为后缘尾缘点的垂直位移，cF为柔性后缘的长度(一般占翼型弦长的20～30%).

假设来流为无粘流［10］，可以采用面元法来计算翼型的翼面压力和升力［11］.下列算例均采用NACA0012翼型，变形后缘长度为弦长的30%.假定柔性后缘和传统后缘的偏转角均为10°(向下)，图1为不同形状后缘的翼型表面压力分布曲线.可以看出，传统后缘在偏转轴处出现压力尖点，而柔性后缘的翼型上、下表面压力分布在变形部分比较平缓，且压力峰值出现在变形起始点之后(压力峰值点后移)，可以预见带有柔性后缘的翼型气流分离点将后移.还可以看出，柔性后缘在翼型后缘部分形成了更大的局部加载，因而在相同的后缘偏角下所产生的升力也就越大(翼型上、下表面压力所围成的面积).

图1 柔性后缘与传统后缘的翼型压力分布

图2(a)为不同形状后缘的翼型升力随着攻角的变化曲线.可看出，在相同的攻角和偏转角下，柔性后缘的翼型升力系数比传统后缘提高了0.27左右;在相同攻角下，产生同样升力所需后缘偏角，柔性后缘比传统后缘小2°.图2(b)为不同形状后缘的翼型俯仰力矩系数随着攻角的变化曲线.柔性后缘的翼型低头俯仰力矩比传统后缘增加了68%左右，是由于柔性后缘在翼型后部形成更大的局部加载造成的.考虑机翼结构的弹性，过大的低头力矩会降低控制面的操纵效率［6］.

图2 不同形状后缘的翼型气动特性(偏转角为10°)

综上所述，柔性后缘给翼型气动特性带来的好处主要有:柔性后缘的翼型表面气动压力分布趋于平缓，产生同样的升力所需后缘偏角小于传统后缘;但是，柔性后缘会产生较大的低头力矩.

2 关节式准柔性后缘的气动特性

图3所示的多关节式准柔性后缘可充分运用现有成熟的控制面结构设计和控制技术，具有低成本、易于结构实现等优点，一旦变形方案在实验室内获得成功，很容易应用到工程实际中去.

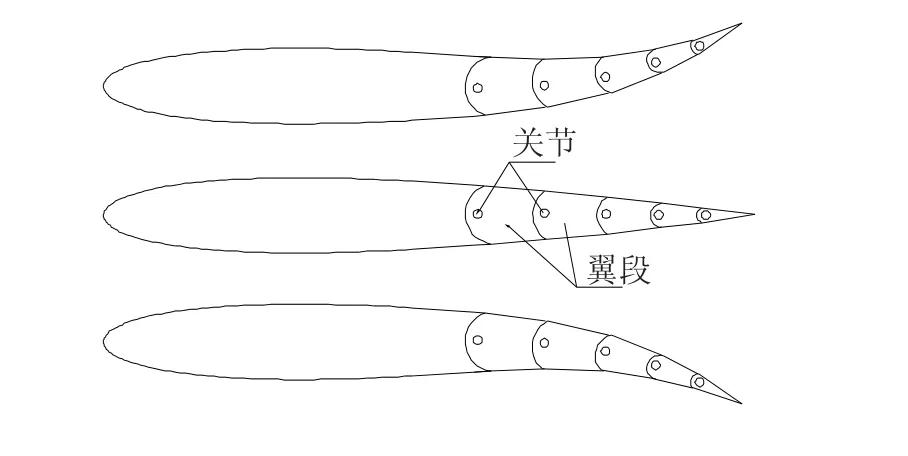
图3 关节式后缘的结构和变形示意图

对于多关节式后缘而言，其后缘偏角不能唯一地确定后缘的变形形状.因为两点之间的直线是唯一的，但曲线可以有很多条.因此，对于多关节式后缘，除了定义等效偏转角外，还要给出各个关节的相对偏转角.

设各个关节的相对偏转角相等，且后缘各片段等长，则相对偏转角与等效偏转角间的关系为

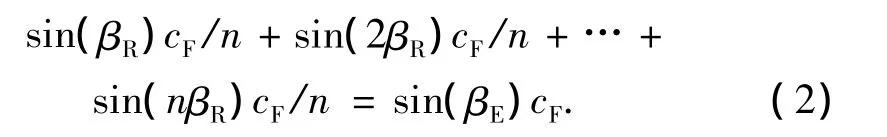
其中:n为后缘关节数，βR为各关节的相对偏转角.假设βR和βE均是小角度，那么相对偏转角可以简化为

由式(3)可以看出，βR＜βE.正是由于后缘采用多关节式形式，各关节的相对偏转角小于传统控制面的偏转角，这样使得变形后的后缘翼型表面趋于光滑.

图4为不同关节数后缘的翼型表面压力分布曲线.可以看出，传统式后缘(1个关节)的翼型表面压力在转轴附近出现较大的尖点，上表面的气流通过转轴位置时要克服很大的逆压梯度，这样会导致气流的过早分离.当后缘采用2个关节时，翼型表面压力在两个转轴附近均出现尖点，但这两个尖点的高度比单节后缘要低得多.以此类推，对于多关节后缘，翼型表面压力在各个转轴附近均出现尖点，但尖点高度随着节数的增加而逐渐降低.当关节数为5时，翼型表面压力的尖点已经非常低了;当关节数为10时，翼型表面压力分布已和柔性后缘相差无几了(图1中的柔性后缘压力分布).同时，产生相同升力所需的后缘偏角随着后缘关节数的增加而减小，如图5，俯仰力矩(低头)是随后缘关节数的增加而逐渐增大的，如图6.

由此可见，后缘的关节数越多，相对偏转角越小，翼型表面曲率的突变程度越低，相应表面的压力尖点越低.但是，多关节式后缘也无法克服柔性后缘带来的俯仰力矩偏大的问题.这个问题可以通过配合前缘控制面的变形来克服.

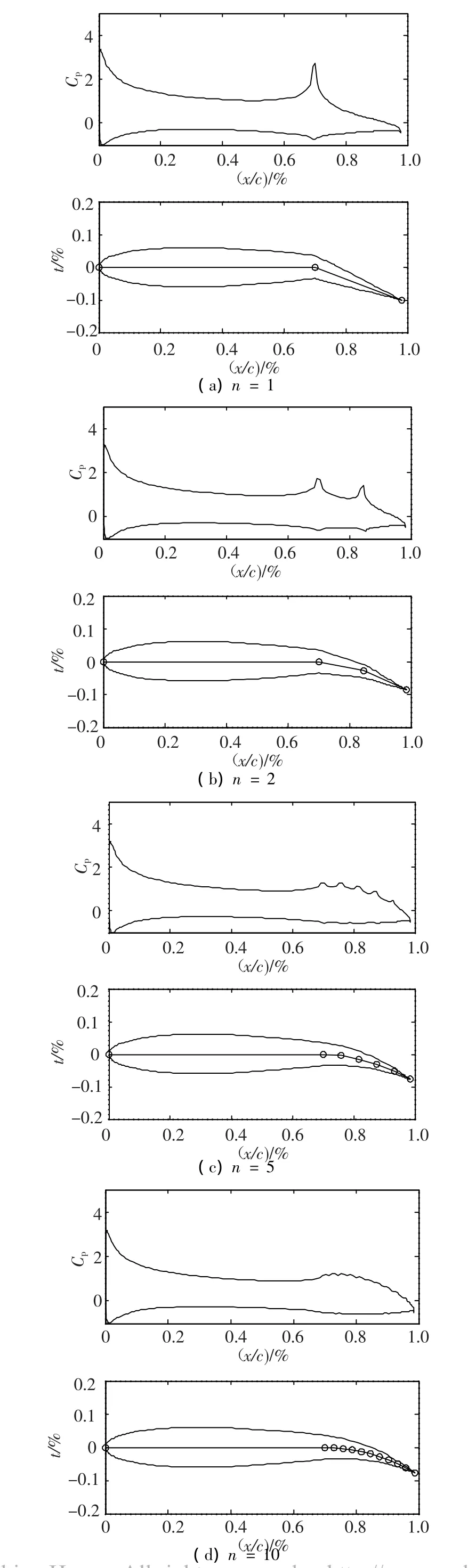
图4 后缘关节数对翼型表面压力的影响(α=0°，CL=1.53)

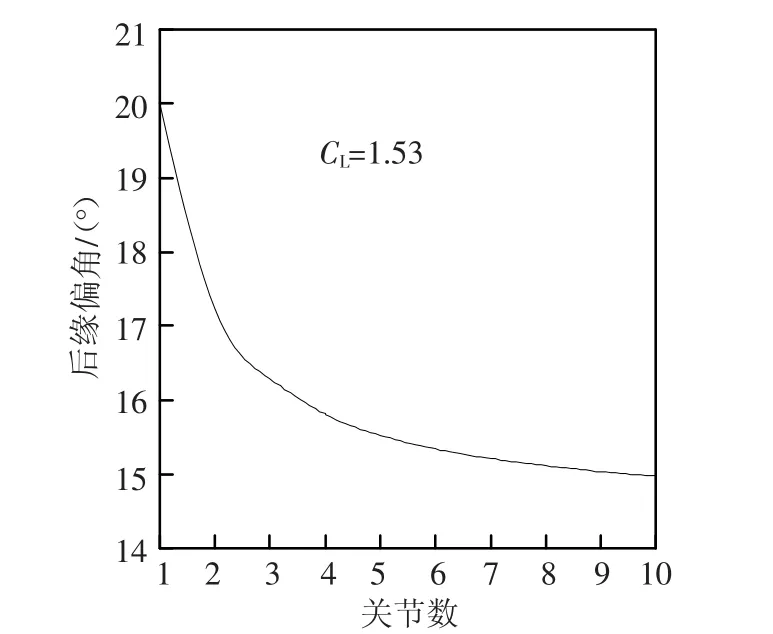
图5 后缘偏角随着后缘关节数的变化

图6 俯仰力矩随着后缘关节数的变化

3 关节式后缘的转轴力矩

气动力作用在关节转轴上的力矩可以通过翼面压力(关节位置到后缘尾缘点)对该关节转轴中心的力矩积分得到.假设各个关节的相对偏转角度相等，且各个翼段同时偏转.图7为第1个关节转轴的气动力矩随着关节相对偏转角的变化曲线.可以看出，转轴力矩随着相对偏转角线性增加;当变形结束后，气动力作用在第1个关节的转轴力矩随着关节数的增加而增大，5关节后缘第1个关节的最终转轴力矩比1个关节后缘(传统偏折式后缘)增大了87%.

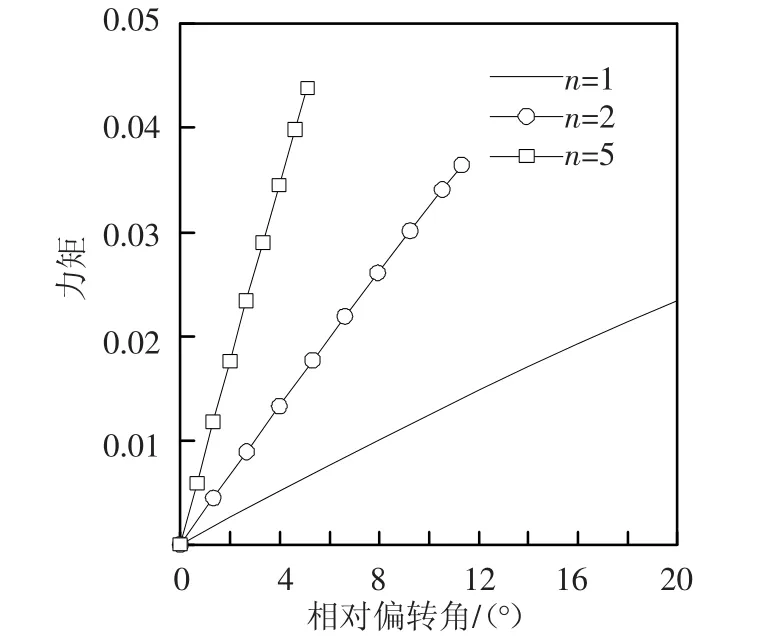
图7 第1个关节的转轴力矩随着相对偏转角的变化

4 结论

柔性后缘的翼型表面气动压力分布趋于平缓，产生同样的升力所需后缘偏角小于传统后缘;但是，柔性后缘会产生比较大的低头力矩.多关节式准柔性后缘充分运用了现有成熟的控制面结构设计技术和控制技术，具有低成本、易于结构实现等优点.关节式后缘的翼型表面压力在各个转轴附近均出现尖点，但尖点高度随着节数的增加而逐渐降低，产生相同升力所需的后缘偏角随着后缘关节数的增加而减小;但是，俯仰力矩(低头)是随着后缘关节数的增加而逐渐增大的，第1个关节的转轴力矩随着关节数的增加而逐渐增大.

虽然多关节式后缘存在关节增多带来重量增加和驱动力矩增大的问题，但可借助复合材料和智能驱动材料来克服.本文的研究成果可直接为柔性后缘机翼的结构设计提供必要的技术指导.

［1］PARKER H F.The parker variable camber wing，NACA－77［R］.［S.l.］:NACA，1930.

［2］邱涛，何刚.自适应机翼—后缘变弯度机翼结构设计原理初探［C］//航空飞行器发展与空气动力学研讨会论文集.北京:中国航空学会，2006:110－114.

［3］ROH J H，KIM K S，LEE I.Shape adaptive airfoil actuated by a shape memory alloy and its aerodynamic characteristics［J］.Mechanics of Advanced Materials and Structures，2009，16(3):260－274.

［4］MONNER H P.Realization of an optimized wing camber by using form variable flap structures［J］.Aerospace Science Technology，2001，5(7):445－455.

［5］POONSONG P.Design and analysis of a multi－section variable camber wing［D］.Maryland:University of Maryland，2004.

［6］杨智春，解江.柔性后缘自适应机翼的概念设计［J］.航空学报，2009，30(6):1028－1034.

［7］ICARDI U，FERRERO L.Preliminary study of an adaptive wing with shape memory alloy torsion actuators［J］.Materials and Design，2009，30:4200－4210.

［8］BARBARINO S，PECORA R，LECCE L，et al.A novel sma-based concept for airfoil structural morphing［J］.Journal ofMaterialsEngineering and Performance，2009，18(5－6):696－705.

［9］GANDHI F，ANUSONTI-INTHRA P.Skin design studies for variable camber morphing airfoils［J］.Smart Mater Struct，2008，17:1－8.

［10］ANDERSON J D.Fundamentals of aerodynamics［M］.New York:McGraw—Hill，1984:189－274.

［11］SANDERS B，EASTEP F E，FORSTER E.Aerodynamic and aeroelastic characteristics of wings with conformal control surfaces for morphing aircraft［J］.Journal of Aircraft，2003，40(1):94－99.