分数阶Fourier域非均匀采样Chirp信号的频谱研究
2010-03-24
(海军航空工程学院 电子信息工程系,山东 烟台 264001)
0 引言
目前数字信号处理理论大多建立在均匀、理想采样信号模型的基础之上,而实际中得到的数字信号一般是非均匀、非理想的采样信号。随着高速采样技术的发展,对非均匀采样信号的研究成为信号处理领域的一个重要的研究内容。非均匀采样是相对于均匀采样的一种采样方法[1]。现实中,由于受到采样设备和被采样信号的限制,均匀采样是相对的,而非均匀采样是绝对的。针对工程实践中经常遇到的Chirp信号,文献[2-4]利用周期性非均匀采样方法给出了非均匀采样 Chirp信号在分数阶Fourier变换下的频谱表达式,分析了其在分数阶域的频谱的特点。本文提出了一种自适应非均匀采样方法,利用此法得到了这类非均匀采样信号在分数阶域的频谱表达式,进一步得到了非均匀采样Chirp信号在分数阶Fourier变换下的频谱表达式,研究了非均匀采样Chirp信号在分数阶的频谱的特点。
1 自适应非均匀采样信号的分数阶Fourier变换
1.1 分数阶Fourier变换
近年来,一种新的时频分析工具—分数阶Fourier变换[5],受到了信号处理界越来越多的关注。它作为Fourier变换的一种广义形式,可以理解为信号的坐标轴在时频平面上绕原点作逆时针旋转。如果把信号的Fourier变换看成其由时间轴逆时针旋转π/2后到频率轴上的表示,则分数阶Fourier变换可以看成将信号由时域逆时针旋转一定的角度到分数阶域上的表示。
信号 x (t)的角度为α的分数阶Fourier变换定义为:
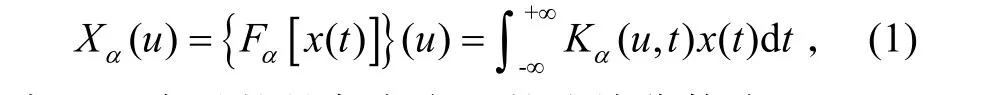
式中:α表示的是角度为α的连续分数阶Fourier变换,变换核为:

有关分数阶Fourier变换的详细介绍,可以参考文献[6-7]。
1.2 自适应非均匀采样信号模型
设模拟信号 x (t)的分数阶Fourier变换Xα(u)是分数阶域中的带限信号[3],即

式中:αΩ是信号 x (t) 在分数阶域的带宽。
自适应非均匀采样流程如图1所示。首先,设定一个采样频率;然后,用此采样频率对信号进行采样。由于信号是时变的,因此在采样过程中必须判断设定的采样频率是否满足采样定理[8]的要求。

图1 自适应非均匀采样流程图
非均匀采样信号模型如图2所示。前n+ 1个采样点的间隔相等,后m个采样点的间隔也相等,即前n+ 1个点和后m个点是均匀采样点,但采样间隔不同,第n个点是分界点。采样频率 f1=1/T1,且使采样频率 f2=1/T2,同样使即满足采样定理的要求。

图2 非均匀采样信号模型
由以上可知,这些非均匀采样序列的采样时刻可以表示为

此非均匀采样序列可写为s={s0,s1}的形式,其中:

将序列1s 右移n+1个位置,得到

式中:z−1表示的是单位延迟算子。
因此,原始的非均匀采样序列可以表示为:

1.3 非均匀采样序列的分数阶Fourier变换
由均匀采样信号的采样定理可以得到[2]:

由分数阶Fourier变换的性质可以得到:

最终可得

当 T1=T2时,

即为均匀采样信号的数字谱表达式。

即变为Fourier 域中的均匀采样频谱表示。该式与文献[9]所得结果一致。
2 非均匀采样Chirp信号的分数阶频谱分析
在工程处理和应用中经常会遇到Chirp信号,如在雷达和声纳的回波信号中。处理Chirp信号的方法很多,其中分数阶Fourier变换是比较理想的方法。
Chirp信号的模型可以表示为:

当 cotα + m0=0时,其分数阶Fourier变换可以表示为:

将式(12)代入式(11)即可得到非均匀采样Chirp信号的分数阶数字频谱:

3 仿真
仿真时选择x (t)=ej(3t2+2t)作为初始信号,信号的观测时间为[0.01 s,4.98 s]。首先,用采样频率f1=25 Hz 对信号进行均匀采样,采样时间为[0.01 s,3 s],采样点数为75个;再用采样频率 f2=50 Hz 对信号进行采样,采样时间为[3 s,4.98 s],采样点数为100个。对非均匀采样Chirp信号进行分数阶Fourier变换后如图3所示(图3中 p=2α / π,以下同)。该变换所用时间为38.92 s。若对该信号进行均匀采样,设定信号的观测时间仍为[0.01 s,4.98 s],采样频率 f=100 Hz,采样点数为498个,其分数阶Fourier变换如图4所示,所用时间为100.33 s。从采样点数和所用时间可以看出,本文所提出的非均匀采样方法和均匀采样方法相比,既减少了存储空间,又满足了实时性要求。而且,对比图3和图4可以明显看到,图3中信号的幅度低于图4中信号的幅度,这是由于信号的分数阶Fourier变换具有能量聚集性,如果信号采样点数少,那么经过分数阶Fourier变换后,信号在分数阶域的幅度必然低。

图3 非均匀采样信号的分数阶Fourier变换

图4 均匀采样信号的分数阶Fourier变换
4 结束语
本文提出了一种自适应非均匀采样方法,并利用分数阶Fourier变换对这类非均匀采样信号在分数阶域的频谱进行了研究,得到了这类非均匀采样信号在分数阶域的数字谱表达式,进一步得到了非均匀采样Chirp信号的分数阶频谱表达式。最后,仿真结果对结论进行了验证。本文所提出的非均匀采样方法,与均匀采样方法相比,尽管信号在分数阶域的幅度有所降低,但是该方法既节省了存储空间,又满足了实时性要求,利于工程上的实现。
[1]汪安民.基于非均匀采样的信号频率检测方法及其实现[D].武汉:华中科技大学,2004:1-15.
[2]李炳照,陶然,王越.非均匀采样信号的分数阶数字频谱研究[J].电子学报,2006,34(12):2146-2149.
[3]RAN T,BING-ZHAO L,et al.Spectral analysis and reconstruction for periodic nonuniformly sampled signals in fractional fourier domain[J].IEEE Trans Signal Processing,2007,55(7):3541-3547.
[4]李炳照,陶然,王越.分数阶Fourier 域上非均匀采样信号的频谱重构研究[J].电子学报,2008,36(6):1202-1205.
[5]OZAKTAS,H M KUTAY M A,ZALEVSKY Z.The fractional Fourier transform with applications in optics and signal processing[M].New York:John Wiley &Sons,2000:1-50.
[6]陶然,齐林,王越.分数阶Fourier变换的原理与应用[M].北京:清华大学出版社,2004:1-20.
[7]TAO R,DENG B,WANG Y.Research process of the fractional Fourier transform in signal processing[J].Sci China Ser F-Inf Sci,2006,49(1):1-25.
[8]OPPENHEIM A V,WILLSKY A S,NAWAB S H.信号与系统[M].2 版.北京:电子工业出版社,2007:514-582.
[9]张卫强,陶然.分数阶傅里叶变换域上带通信号的采样定理[J].电子学报,2005,33(7):1196-1199.
