一类带θ(t)型核的奇异积分算子的有界性

陈跃辉，叶晓峰，刁俊东

(华东交通大学基础科学学院应用数学，江西南昌330013)

因为左边的式子在r和x中是一致有界的，且由引理中的增长条件可知上面的第一个和第三个式子也是一致有界的，因此

1 介绍及其定义

近年来，奇异积分算子得到了广泛的研究，并取得了丰硕的成果，尤其是随着一些空间分解理论的建立，它们在一些空间上的有界性问题得到了解决。1985年彭立中在文献[1]中引进了具有深刻微分方程背景的θ(t)型Calderón-Zygmund算子，兰家诚在文献[2]和[3]中分别研究了具有θ(t)型Calderón-Zygmund核的多线性奇异积分极大算子的Lp-有界性和型Calderón-Zygmund核的多线性振荡奇异积分算子的Lp-有界性的充分条件，2007年Chang Derchen和Li Junfeng在文献[4]中得出了型Calderón-Zygmund算子的加权估计，2008年吴田峰等在文献[5]中研究了型Calderón-Zygmund算子与BMO函数生成的交换子在空间上的有界性，2009年马丽娜在文献[6]中讨论了型Calderón-Zygmund算子与Lipschitz函数生成的交换子在Lebesgue空间及Hardy空间上的有界性，同年Chen Jiahong在文献[7]中得出了具有Calderón-Zygmund核的多线性振荡算子的加权Lp-有界性，但对于θ型Calderón-Zygmund算子在Lipschitz空间上的有界性问题的讨论还没有，为了得出型Calderón-Zygmund算子在Lipschitz空间上的有界结论，以便将这些有界结论应用到奇异积分算子的研究中，这里我们将主要考虑当K满足型条件时，Calderón Zygmund积分算子在μ为非双倍测度时，算子Tε在Lipschitz空间上的有界性。

μ是一个有限的Borel测度，并且满足n-维增长条件:存在n＞0，A＞0可使得对于所有以r为半径的球Br，所有的r都有是一个测度μ满足n-维增长条件的有限测度空间，是一个度量空间。

设0＜β＜1，如果f∈Λβ，则

定义2 如果存在常数c1，c2，使得:

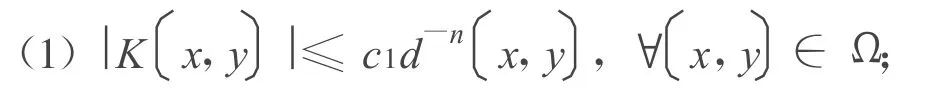
2 定理，引理及其证明

定理的证明

首先，由1∈Λβ可知条件(b)可推出条件(a)。接下来，我们证明条件(a)也可推出条件(b)，为了证明条件(a)也可推出条件(b)，首先对于所有的x∈X，观察发现，当0＜r1＜r2＜∞时，我们有

因为左边的式子在r和x中是一致有界的，且由引理中的增长条件可知上面的第一个和第三个式子也是一致有界的，因此

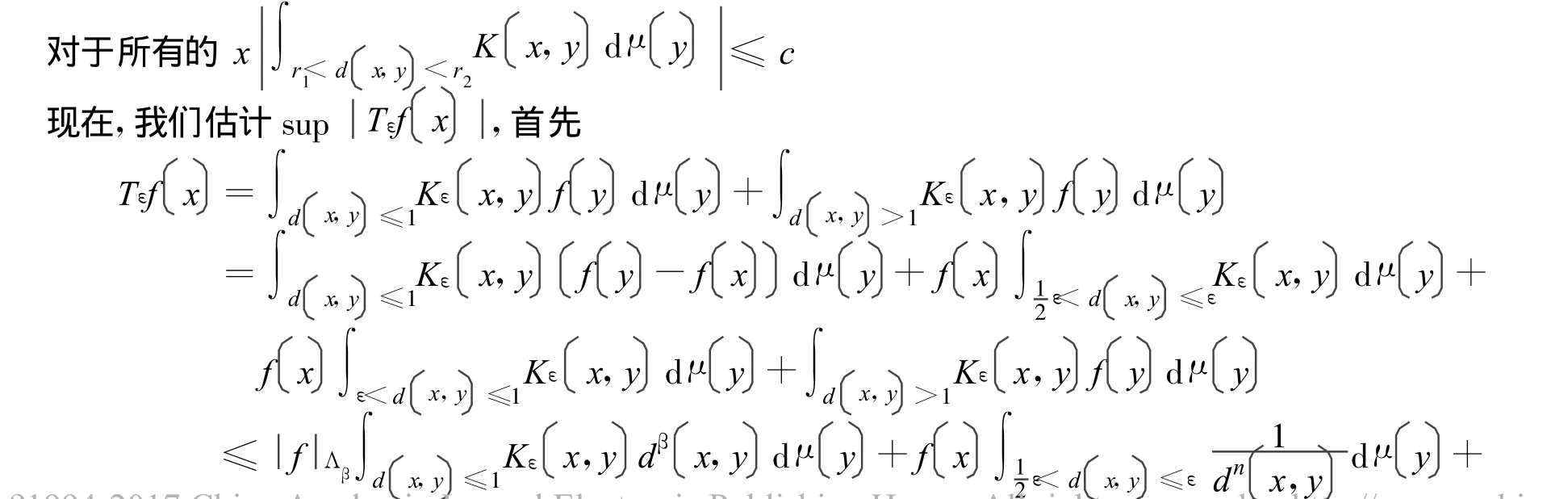
[1] 彭立中.广义Calderón Zygmund算子及其加权模不等式[J].数学进展，1985，25(02):12-16.

[2] 兰家诚.具广义Calderón Zygmund核的多线性振荡奇异积分极大算子的有界性[J].数学年刊，2005，26(6):799-812.

[3] 兰家诚.广义Calderón Zygmund核的多线性振荡奇异积分算子的Lp-有界性[J].应用数学学报，2006，29(2):566-576.

[4] Chang Derchen，Li Junfeng.Weighted scale estimates for generalizedCalderón Zygmund type operators[J].Contemporary Math，Amer Math Soc，2007，44(5):61-70.

[5] 吴田峰.θ(t)型Calderón Zygmund算子交换子的有界性[J].绵阳师范学院学报，2008，27(8):306-314.

[6] 马丽娜.广义Calderón Zygmund算子交换子的有界性[J].高校应用数学学报，2009，24(4):453-461.

[7] Chen Jiahong.Weighted Lp-boundedness ofmultilinearoscillatory singular integralwithgeneralized Calderón-Zygmundkernel[J].Journal of the Graduate School of the Chinese Academy of Sciences，2009，26(5):852-866.

[8] EDUARDO G A.Boundedness on inhomogeneous Lipschitz spaces of fractional integrals，singular integrals and hypersingular integrals associated tonon-doub lingmeasures.[J].Math.CT，2008，106(3):956-980.