对数零相位谱在雷达目标识别中的应用研究

冷家旭,黄惠明,龙 方

(北京跟踪与通信技术研究所,北京 100094)

1 引言

高分辨一维距离像(HRRP)是雷达接收到的目标强散射点子回波沿雷达视线方向的投影矢量和,它包含了目标沿距离向精细的几何结构特征,对目标分类识别十分有价值。但是H RRP对目标的姿态变化和距离向的平移变化都很敏感。为抑制平移敏感性问题,人们提出了多种平移不变特征,如幅度谱、功率谱、零相位谱等。相比于幅度谱、功率谱,文献[2]提出的零相位谱保留了除线性相位以外的所有相位信息,且计算难度不大。

在此基础上,结合对目标高分辨距离像产生原理的分析,本文提出一种对数零相位谱最小距离识别方法——提取目标HRRP的对数零相位谱特征,利用线性判别分析进行维数压缩,并在最小欧氏距离与最小马氏距离准则下对飞机目标进行分类识别。外场实测数据的仿真结果表明对数零相位谱特征识别性能优于功率谱与幅度谱特征,验证了本文方法的可行性与有效性。

2 对数零相位谱的定义

所谓零相位谱,即是将高分辨实距离像x(n)的频谱X(m)=[X0 X 1 ejφi…XN-1 ejφN-1]的每根谱线相位φi(i=0,1,…,N-1),减去第1根相位非零谱线的相位φ1的0～N-1倍,从而使X(1)的相位置零,具体形式为[3]:

对数零相位谱是通过零相位谱取自然对数获得的,定义为:

定义1 设XZPP(m)为一维距离像序列x(n)的零相位谱,则称

是序列x(n)的对数零相位谱。

根据零相位谱的定义与性质,容易证明,对数零相位谱同零相位谱一样,能够完全去除信号中的线性相位并保留其他相位信息,具有平移不变性。通过下节的推导还可以看出,对数零相位谱能利用简单的最小距离判决准则实现目标分类识别,并且具有明确的物理意义。

3 分类方法

3.1 对数零相位谱最小距离分类原理

高分辨雷达通常工作在高频区,目标可以用散射点模型表示。设当目标姿态角为θ时,雷达信号在目标面向雷达表面r(x,y,z)处引起的散射点分布函数为h,θ)[4],其中r为目标几何中心到该处的位置矢量。

若雷达发射线性调频信号:S(t)=rect(t/Tp)◦ej2π(fct+γt2/2),则目标回波经dechirp脉压处理后得到的一维实距离像可表示为[5]:

式中,Tp为脉宽,γ为调频率,R ref为解线频调的参考距离,R=|R0+r|为散射点到雷达距离,R0为雷达到目标几何中心的距离矢量。注意到远场条件R0≫r,近似有R=R0+r cosφ,φ=∠(R,r)。

对Sr(t)进行时域采样(采样频率为fs),并将式(3)两边进行DFT,化简可得:

式中,R0=R0-R ref(即:R ref的影响可以通过平移坐标消除),H(m,θ)为目标散射函数h(r,θ)的空域离散Fourier变换,积分面s是处在雷达波束内雷达可见的目标曲面。

式(3)表明,目标实距离像的频谱可分为3部分,第1项P(m)仅与雷达发射信号有关,第2项exp[j(4πf,γm/Nc)R0]是目标相对雷达平动引起的线性相位项,而第3项H(m,θ)则包含了目标的特性信息,是HRRP目标识别的根本依据。

将Sr(m;θ)转换到对数零相位谱域,可以消除目标平动引起的线性相位,则有:

假设雷达观察到目标h1(r,θ1)和h2(r,θ2)的回波分别为s1(t;θ1)和s2(t;θ2),在对数零相位谱域相减,可得:

式(6)表明,不同目标雷达回波的对数零相位谱的距离测度(如欧氏距离、马氏距离等),可以作为度量和判断不同目标相似程度的依据。因此,对数零相位谱最小距离分类方法适用于雷达HRRP飞机目标识别。

3.2 对数零相位谱最小距离判决准则

根据上述分析可知,对数零相位谱最小距离判决准则可表述如下:

假设有C类不同目标,其姿态角为θij,i∈NC,NC={1,2,…,C},j∈Di,Di={1,2,…,Ni},Ni为第i类目标划分的姿态角域个数。用它们的平均对数零相位谱log zpp (si(t;θij))作为比较模板,对于待识别目标的距离像s(t;θ),如果存在某个确定的k∈NC,l∈Dk,对∀i∈NC,j∈D i有:则认为目标是姿态角为θkl时的第k类目标。

在本文中,取d(x1,x2)分别为样本点x1、x2的欧氏距离与马氏距离,即:

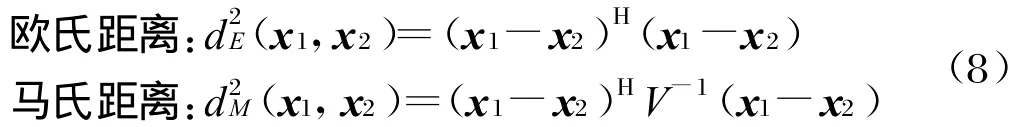
4 算法仿真

4.1 外场实测实验数据介绍

本文采用雷达实测飞机数据进行仿真识别。该数据是取自国内某研究所逆合成孔径C波段实验雷达的ISAR测量飞机数据,其脉冲重复频率为400Hz,信号带宽为400MH z;采用Dechirp接收,转换后信号的采样频率为10MH z。试验飞机有三种,“雅克-42”为中大型喷气飞机,“奖状”为小型喷气飞机,“安-26”为中小型螺旋桨飞机。

根据数据中航迹信息可以预先估计出飞机姿态角,本文选用“雅克-42”的第1段,“奖状”的第2、4段以及“安-26”第1、3段作为训练样本,以10°为间隔划分姿态角域,适当抽取后生成18个训练样本库,每个样本库包含500个距离像。测试样本来自其它段数据,每类飞机取10000个测试距离像。

4.2 仿真流程与结果比较

因为距离像的能量集中在信号的低频部分,不同目标距离像间的差异信息也主要集中在低频分量上。因此,本文首先将提取的对数零相位谱进行低频截短,再利用线性判决分析(LDA)[6]以及最小欧氏、马氏距离分类器进行目标识别。作为对比,试验还截取了相同频段的功率谱与幅度谱特征,具体算法仿真流程如图1所示。

表1、表2为不同截取维数时对数零相位谱、功率谱与频谱幅度三种特征的识别性能比较,其中表1使用最小欧氏距离分类器,表2使用最小马氏距离分类器。根据频谱幅度的对称性,用于比较的低频分量最大截取维数为128。

图1 仿真算法流程

表1 不同截取维数时识别性能的比较(最小欧氏距离分类器)

表2 不同截取维数时识别性能的比较(最小马氏距离分类器)

从表1、表2中可以看出,截取维数高于2维时,对数零相位谱的识别率均高于同频段的另外两种特征。这是由于频谱相位中包含了更多的目标形状信息,功率谱与幅度谱丢失了全部相位信息,而对数零相位谱则保留了除线性相位以外的所有相位信息,因此其识别性能优于另外两种特征。另外,每种特征的识别率均随着维数增加先上升后略有下降,这是因为距离像的鉴别力主要集中在低频分量上,高频分量则包含了更多的幅度突变和噪声杂波等干扰,低频分量的增加能够提高识别率,而有害高频信息的引入将导致识别率下降。但FDA能在压缩维数的同时聚集同类、分散异类,在一定程度上减弱了高频分量的干扰,使识别率下降幅度不大。

比较表1、表2的数据,不难发现,相同条件下最小马氏距离分类器的识别性能优于最小欧氏距离分类器。这是由于马氏距离在计算过程中考虑了类内样本矢量中每个特征点的方差,在计算距离时依据方差大小对各特征点分配不同的权值,达到减弱大方差特征点影响的目的,因而其识别率高于欧氏距离分类器。但也正是因为需要计算类内样本的协方差矩阵,马氏距离的计算量较大,如表3所示,其平均时耗均高于相同条件下的欧氏距离分类器,识别性能的提升是以牺牲运算量为代价。

表3 识别性能与时耗比较,维数为32

综合上述三种特征的识别性能与低频分量截取维数的关系以及识别过程的平均时耗,对数零相位谱特征在平均识别率、运算量等方面均表现了出色的性能,不失为HRRP目标识别中的一种合理选择。而基于欧氏距离与基于马氏距离的判决准则各有利弊,在工程应用中可根据实际情况加以选择。

5 结束语

高分辨距离像的频谱相位包含了大部分目标信息,对数零相位谱特征不仅能够保留这些信息,而且具有平移不变性。本文提出对数零相位谱最小距离目标识别方法,将对数零相位谱特征成功地应用于雷达目标识别领域中。在对外场实测数据的仿真试验中,比较了最小欧氏距离与最小马氏距离两种判决准则下对数零相位谱特征的识别性能,同时将其与功率谱、幅度谱进行横向对比,验证了该方法的可行性与有效性。■

1 Xing M,Bao Z,Pei B.The properties of high-resolution range profiles[J].Optical Engineering,2002,41(2):493-504.

2 曹向海,刘宏伟,吴顺君.基于零相位谱的雷达目标识别[J].现代雷达,2007,29(9):48-55.

3 Pajd la T,H lavac V.Zero phase representation of panoramic Images for image based localization[C].Proc.8th Int.Con f on Computer-analysis of images and patterns,Berlin,Springer,1999:550-557.

4 裴炳南.高分辨雷达自动目标识别方法研究[D].西安:西安电子科技大学,2002.

5 保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2006.

6 刘本永.子空间法雷达目标一维像识别研究[J].电子与信息学报,2004,26(7):1137-1143.