平面二维浅水模型在枢纽施工期行洪与通航研究中的应用

2010-03-21王振华

湖南水利水电 2010年5期

王振华

（永州市水利水电勘测设计院永州市425000）

低水头水利枢纽常修建于平原河流，工程施工导流方案一般选择分期围堰法，各期围堰布置型式对束窄河段的行洪与通航有着重要影响。初步设计中常利用施工期束窄河段过流面积估算其平均流速，并根据不同围堰布置型式的侧收缩系数及流速系数估算上下游水位落差，从而分析导流方案对行洪与通航的影响。但对于平原地区常见的微弯分汊河流，施工期分流比发生改变，河床宽浅不一，边界复杂，不易确定主汊流量，很难利用经验公式准确计算汊道束窄河段平均流速及水位差，无法分析流场分布对通航的影响。虽然可进行物理模型试验，但其存在周期长、成本高、不易修改边界的缺点。

针对上述问题，下面以某拟建水利枢纽工程为背景（枢纽河段河势如图1所示），通过数学模型分析不同的围堰布置方案对坝址处微弯分汊河段洪水期水位壅高及束窄河段流场的影响，为施工导流方案设计提供参考。

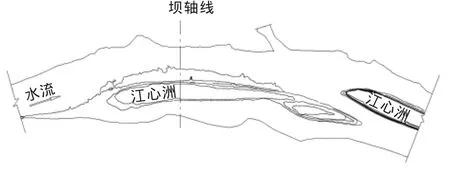
图1 枢纽河段河势图

1 数学模型计算及结果分析

1.1 控制方程

工程所在河段为宽浅水域，水力参数在垂直方向的变化明显小于水平方向的变化，故忽略垂向流速及垂向加速度，使水压力接近静压分布，并根据Boussinesq假定将三维N-S方程沿水深方向积分平均即可得平面二维浅水运动控制方程。忽略科氏力及水面风应力，其在笛卡尔坐标系下可表示为：

水流连续方程：

式中h——水深；ux和uy——分别为沿水深积分的平均流速在x、y方向的分量；z0——河床高程；g——重力加速度；vt——紊动粘性系数；ρ——水的密度；n——曼宁糙率系数。

离散方法采用有限单元法，运用Galerkin加权余量法把浅水方程离散成非线性代数方程，然后采用Newton-Raphson方法求解。离散区域内采用三角形6节点等参单元和四边形8节点等参单元相混合。网格步长为（10～50）个万单位。

1.2 模型的计算分析

1.2.1 模型的率定

模型采用枢纽河段实测地形，模拟范围包括坝址上游4 km及下游8 km河段。并利用原型洪、中、枯三级流量观测资料率定和验证模型，结果表明模型水面线、断面流速分布及分流比均与原型吻合较好，可应用于施工期水动力模拟。

1.2.2 模型计算方案的确定

枢纽河道深泓线位于左汊左岸一侧，形成宽约300 m的深槽，河床平均高程约为15 m左右。左汊靠近江心洲一侧为宽约400 m的漫滩，高程在（20～30）m之间。为提高枢纽河段行洪能力，计算模型将左汊漫滩开挖至20 m高程，且右汊工程可在枯水期完成，洪水期过水。在此基础上分析主汊束窄河段行洪能力。计算洪水流量采用该河段两年一遇洪水流量。

计算内容从以下两方面考虑确定：

（1）由于河床深槽靠近左汊左岸，因此需分析在过流面积相等情况下，漫滩开挖后束窄河段分别位于左汊左侧和左汊右侧时（图2）对水位壅高的影响，以便于合理设计微弯分汊河道各期围堰位置。根据河床地形计算得，束窄河段位于左汊左侧、宽度分别为200 m和250 m时，其过流面积与束窄河段位于左汊右侧、宽度分别为250 m和320 m时相等。故对此四种方案进行计算分析。

图2 两种围堰布置方案（左：方案1，右：方案2）

（2）工程中常采用钢筋混凝土材料将纵向围堰做成直墙型，并作为永久建筑物与闸墩相结合。但围堰附近会形成回流区，不利于束窄段的行洪与通航。改善回流区的方法之一是改变纵向围堰线型，使束窄河段水流过渡平缓。因此，需分析不同纵向围堰型式对水位壅高及通航的影响程度，进而合理设计施工导流方案。计算选取束窄宽度分别为200，250，300，350，400 m情况下，两种不同纵向围堰型式（图3）的水位壅高及通航水流条件。

图3 两种纵向围堰型式（左：直线型，右：流线型）

1.3 计算结果分析

（1）不论束窄河段位于左汊左侧（方案1）还是右侧（方案2），当束窄河段溢流面积相等时，水位壅高值基本一致（表1）。说明左汊漫滩开挖以后，洪水期微弯河道及河床深槽对主流影响不大。因此，当各施工期主汊束窄河段溢流面积相近时，即可保证各期水位壅高较均衡，从而使施工期水位壅高值达到最低。

表1 不同围堰布置方案对水位壅高影响m

（2）从表2可看出，随着溢流宽度的增加，水位壅高逐渐减小。在相同溢流宽度下，流线型纵向围堰能够降低水位壅高，尤其是在溢流宽度较小时，水位壅高降幅较大。说明溢流宽度较小时回流区对上游水位壅高影响较大。因此，在工程中当溢流宽度受通航要求、工程量、施工强度等因素影响，调整范围受限时，可通过优化纵向围堰线形来有效提高行洪能力。

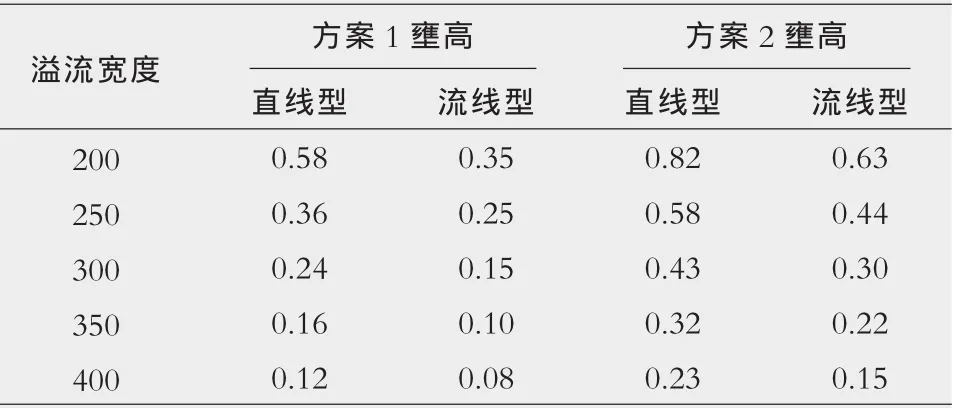
表2 不同围堰布置型式的水位壅高m

（3）由各工况流场分析可知，左汊主流在进入束窄河床时，即在上游纵向围堰端部处，由于水流急剧束窄挤压，产生较大横流，影响范围较大。当束窄河床位于左汊右侧时，对于不同的溢流宽度和纵向围堰线形，河床束窄处水面横向流速分布如图4所示。流线型围堰使水流过渡更加平缓。在靠近围堰处，最大可使横流降低1.0 m/s左右，且横流大于0.3 m/s的宽度约为（150～200）m，比直线形纵向围堰工况减少（50～100）m。当束窄河床位于左汊左侧时，同样具有类似规律。因此，为保证航行安全，应优化纵向围堰线形，同时应使航道距离围堰150 m以上。

2 工程实例分析

2.1 导流方案的确定

（1）各期围堰布置设计。拟建枢纽工程经可行性论证，其主要建筑物布置为：左汊从左至右依次为船闸、泄水闸及电站厂房，右汊为泄水闸。左汊27孔泄水闸堰顶高程19.00 m，孔口净宽20 m，右汊19孔泄水闸堰顶高程25.00 m，孔口净宽14 m。

图4 不同工况河床束窄处水面横向流速分布

工程主要开发目标为改善航运条件与水环境，电站发电效益主要为解决运行期的运行成本，因此，施工导流方案选择的总原则是确保施工期不断航、尽量减少施工期库区水位壅高。考虑优先对船闸施工，围堰布置方案为：一期围堰围左汊左侧船闸及部分泄水闸，束窄河段临时航道通航，并利用枯水期对右汊泄水闸施工。二期围堰围左汊右侧，已建船闸通航。

（2）纵向围堰位置确定。左汊总溢流宽度约为700 m左右，根据数模结论①，当各期束窄河段宽350 m时，可使过流面积基本相等，从而使施工期水位壅高值最小。但是，一期束窄河段需要开挖临时航道及漫滩，考虑到施工进度及工程量，为尽快完成临时航道开挖，保证施工初期不断航，临时航道必须选在距离洲岸约300 m处。根据数模结论③，为保证通航安全，临时航道应至少距离纵向围堰150 m左右。因此，将一期束窄河段宽度初步定为450 m。与此对应的二期溢流净宽仅为200 m，是施工期行洪能力的控制工况，且该溢流宽度受一期通航条件及工程量影响不益做大幅度增加。根据数模结论②，应优化二期纵向围堰线形来提高束窄河段行洪能力。

2.2 物理模型试验分析

围堰为土石过水围堰，挡水标准为两年一遇洪水流量。并采用该流量研究行洪与通航。

二期由左汊10孔已建泄水闸过流，净宽为200 m。当纵向围堰设计为直线型作为闸墩的一部分时，闸前形成回流区（图5左），水位壅高值为62 cm。设计标准要求不超过45 cm。故该方案行洪能力不满足要求。然后试验增加了20 m、40 m溢流净宽，壅高值降为：57 cm、52 cm，仍不符合要求。可见仅在局部范围内增加溢流宽度是不能有效提高行洪能力的。通过采用增加20 m净宽并将纵向围堰改为折线型方法，改善回流（图5右），壅高值降为42 cm，符合设计要求。可见在溢流宽度较小时，调整纵向围堰型式能够有效降低水位壅高，与数模结论相吻合。

图5 二期不同纵向围堰线形闸前流场

与二期对应的一期溢流宽度约为420 m，当采用直线型纵向围堰时，束窄河段形成宽约150 m的回流区，河床束窄处临时航道局部横流达到0.8 m/s，不利于船舶航行安全。改为流线型纵向围堰后，回流区宽度仅为约70 m宽，局部横流约0.45 m/s，基本不影响通航。因此，该围堰布置方案满足各期行洪与通航要求。