混响室搅拌器位置优化的数值分析

崔耀中,魏光辉,范丽思,万浩江,刘小强

(军械工程学院强电磁场环境模拟与防护技术国防科技重点实验室,石家庄 050003)

1 引 言

混响室是一种新型的电磁兼容测试场地,通过屏蔽腔体内一个或多个搅拌器的不断转动,改变电磁场的边界条件[1-3],以产生一个统计意义上的均匀场,它具有 Q值高、成本低、测试空间大等优点[4-5]。搅拌器作为混响室的重要组成部分,其配置直接影响其改变边界条件的能力,进而决定混响室电磁场的统计均匀性[6-7]。而场均匀性是评价混响室性能的决定性指标,国内外学者对此进行了大量的相关研究[8-9]。但这些因素的改变通常是根据工程技术人员经验,并没有达到最优解,且工程应用价值受限。

本文采用基于矩量法(MOM)电磁仿真软件FEKO建立了配备双搅拌器的混响室仿真模型,并结合遗传算法(GA)对混响室搅拌器位置进行优化,以得到统计均匀性较为理想的电磁测试环境。通过优化计算,得到了搅拌器位置的最优解以及相应的表征混响室场均匀性的电场标准偏差值。

2 仿真建模

混响室模型主要包括屏蔽腔体、发射天线和搅拌器,如图1所示。屏蔽腔体大小为9.92 m(长)×7.44 m(宽)×4.06 m(高);发射天线为工作带宽57.08～93.75MHz的对数周期天线,本文选择工作频率80MHz进行研究;搅拌器采用两个大小不同的Z型结构搅拌器,其中大搅拌器横向放置,小搅拌器竖直放置。FEKO建立的混响室仿真模型内部结构如图2所示。

图1 混响室示意图Fig.1 Sketch of a reverberation chamber

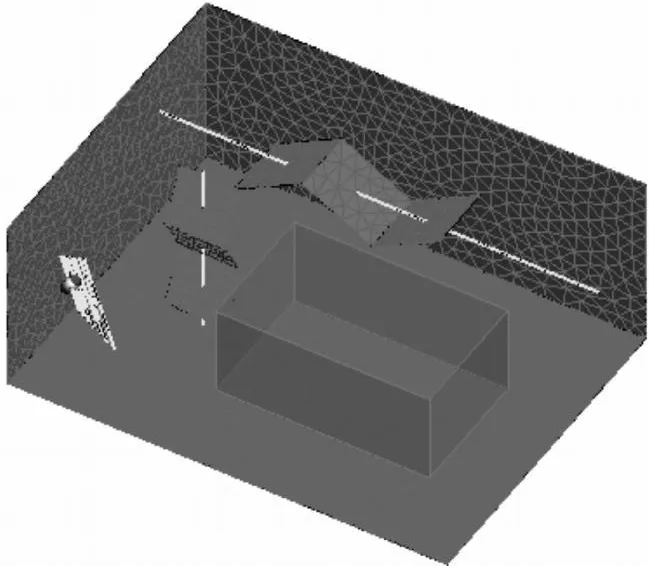
图2 仿真模型内部结构Fig.2 Inner structure of simulation model

3 目标函数及综合评价函数计算

遗传算法通过调用FEKO建立混响室仿真模型,优化双搅拌器在混响室中的位置,使得评价混响室场均匀性的电场标准偏差在满足标准IEC61000-4-21[10]要求的基础上尽可能小,测试区域8个顶点位置处对输入功率归一化的最大电场值的标准偏差越小,说明测试区域场均匀性越好。测试区域距离腔室6个面、天线及搅拌器的最短距离应大于λ/4或者1 m,λ为最低工作频率波长。在此选择矩形测试区域坐标区间 x∈[3.5,6.44],y∈[4.1,8.92],z∈[1,3.06]。

在搅拌器旋转一周内,记录测试区域8个顶点位置在正交轴上的最大电场强度Emaxik(i代表正交轴x、y、z方向,k代表顶点位置1～8)及平均输入功率 Pinput,求出各顶点处Emaxik对Pinput的归一化最大电场值:

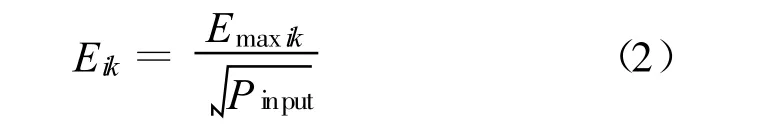
分别对Eik在8个顶点位置求平均值〈〉8及对 Eik在8个顶点,每个顶点3个正交轴位置求平均值〈〉24:

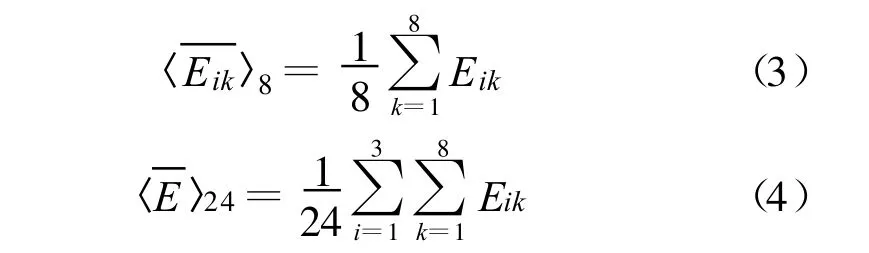
各正交轴向归一化最大电场值标准偏差:

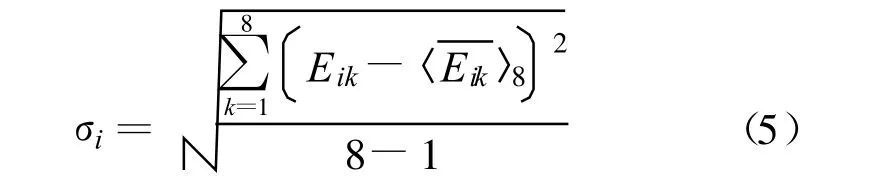
8个顶点,每个顶点3个正交轴的归一化电场最大值Eik标准偏差:

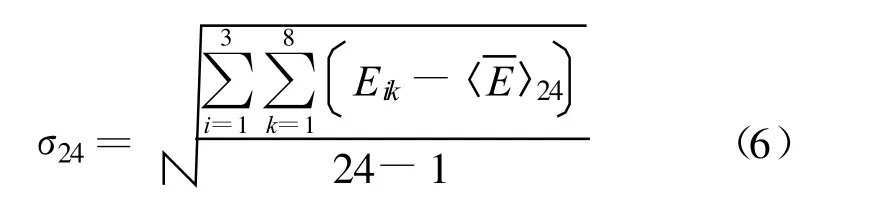
标准偏差σ相对于平均值可以表示为单位为dB的量:

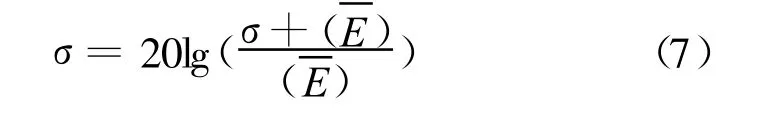
将各轴向电场标准偏差 σx、σy、σz及总标准偏差σ24作为遗传算法优化多目标函数。根据多目标优化问题的权重系数变换法[11],在此将综合评价函数即适应度函数定义为各目标函数的加权和,即综合评价函数:

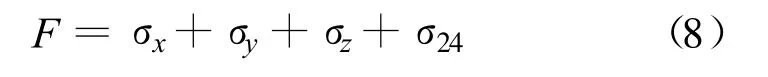
这样将多目标优化转化为单目标优化,即F※min,F 越小 ,即 σx、σy、σz及 σ24越小,说明测试区域场均匀性越好。根据标准IEC61000-4-21(如表1所示)的场均匀性限值,当工作频率在80MHz时,可用工作区的标准偏差σ应低于4dB。

表1 场均匀性限值Table 1 Field uniformity tolerance requirements

4 优化计算

优化过程中,遗传算法调用FEKO建立的混响室仿真模型,待FEKO完成对混响室的数值分析后再返回遗传算法,如图3所示。在此采用遗传算法对横搅拌器与腔体右墙距离d1及竖搅拌器与腔体后墙距离d2进行优化,如图4所示。同时测试区域在优化过程中不变。

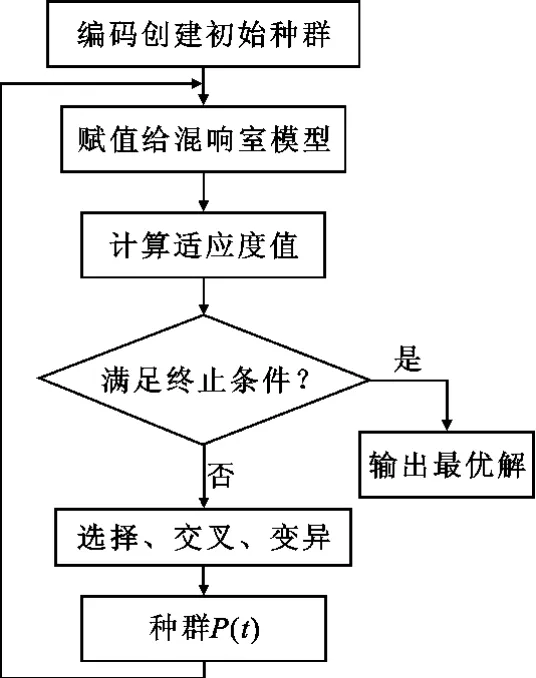
图3 优化流程图Fig.3 Flowchart of optimization

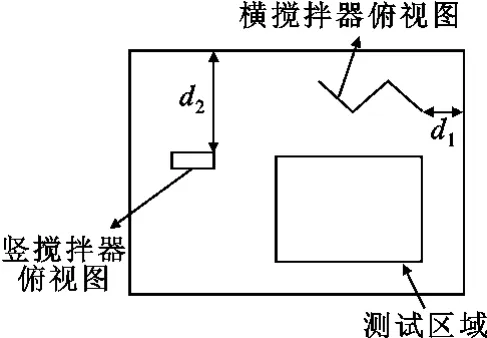
图4 搅拌器初始位置Fig.4 Initial position of stirrer

具体过程如下:

(1)采用实数编码方式随机生成一组初始个体作为初始群体P(0),在此选择种群个体数为30;

(2)程序调用混响室仿真模型,将各个个体值赋给混响室计算模型中的变量d1和d2,并进行混响室数值分析计算;

(3)程序读取仿真结果文件,并计算各个个体的目标函数值及适应度值;

(4)选择操作。根据各个个体的适应度值,采用随机遍历抽样(SUS)选择法,从种群P(t)中选择优良的个体遗传到下一代群体P(t+1);

(5)交叉操作。采用均匀交叉方式首先使种群P(t)中的个体随机配对,之后将两两配对的个体以0.8的交叉概率Pc相互交换部分基因,并将改变基因的个体遗传到下一代种群P(t+1);

(6)变异操作。按照高斯近似变异方式首先在种群P(t)中随机选择一个个体,对于选中的个体按照0.1的变异概率Pc改变某一个或某一些基因座上的基因值为其它的等位基因,并将改变基因的个体遗传到下一代种群P(t+1);

(7)终止条件判断。若进化代数t不大于最大进化代数,转到步骤2,否则将具有最小适应度的个体作为最优解输出,终止运算。

5 优化结果及分析

初始群体P(0)中部分个体以及相应各轴向电场标准偏差、总标准偏差及适应度值如表2所示。初始及优化计算得到的发射天线位置、各轴向电场标准偏差、总标准偏差及适应度值如表3所示,优化后搅拌器位置如图5所示。

表2 初始群体部分个体及相应标准偏差值Table 2 Part of individual in initial population and corresponding standard deviation

表3 优化前与优化后结果比较Table 3 Comparison between initial and optimum

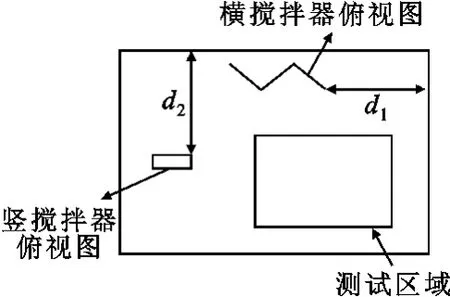
图5 搅拌器最优位置Fig.5 The optimum position of stirrer

从图4和图5可以看出,优化后横搅拌器向中间移动,竖搅拌器向前移动,与发射天线的距离变小。由表2可知,搅拌器位置变化时,测试区域电场标准偏差随之变化,说明搅拌器位置影响测试区域场均匀性。由表3可知,初始状态测试区域电场标准偏差值较大,且 σx、σz大于4dB,不满足标准IEC61000-4-21要求;优化后测试区域场标准偏差明显减小,满足标准IEC61000-4-21的要求。综合评价函数F较初始状态下降了45.4%;各轴向电场标准偏差分别下降了47.4%、20.1%、57.1%,且σy、σz已经小于2dB;σ24下降了44.0%,说明优化后测试区域场均匀性较优化前有所改善。

搅拌器通过转动不断改变混响室边界条件,使谐振频率及模结构发生变化,多个不相关的模结构就产生了多个独立的场分布结构,从统计意义上讲,独立样本越多场分布越均匀。对搅拌器位置进行优化,本质是为了增加独立采样点。从优化结果可知,搅拌器位置优化后,改善了场均匀性,说明提高了搅拌器的搅拌效率,增强了其改变边界条件的能力。

6 结 语

本文通过将遗传算法与混响室数值模拟相结合,研究了搅拌器位置对混响室测试区域场均匀性的影响。研究过程表明:

(1)搅拌器作为混响室内重要组成部分,其位置变化时,混响室测试区域场均匀性随之变化,这是由混响室内电磁场分布不尽相同,从而不同位置的搅拌器改变边界条件的能力不同造成的;

(2)通过优化搅拌器的位置,即提高搅拌器增加混响室独立采样点的能力,各轴向电场标准偏差分别下 降 了 47.4%、20.1%、57.1%,σ24下 降 了44.0%,提高了测试区域场的均匀性,从而提高了混响室用于电磁兼容测试时的准确度。

[1] 丁坚进.混响室理论、设计和测试[D].北京:北京交通大学,2006.DING Jian-jin.Theory,measurement and design of reverberation chamber[D].Beijing:Beijing Jiaotong University,2006.(in Chinese)

[2] Christian Bruns,Ruediger Vahldieck.A closer look at reverberation chambers 3-D simulation and experimental verification[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(5):612-626.

[3] Kent Madsen,Paul Hallbjorner,Charlie Orlenius.Models for the Number of Independent Samples in Reverberation Chamber Measurements With Mechanical,Frequency,and Combined Stirring[J].IEEE Antennas and Wireless Propagation Letters,2004(3):48-51.

[4] David A Hill.Boundary Fields in Reverberation Chamber[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(2):281-290.

[5] 袁智勇,李暾,陈水明,等.混响室设计与校准测试[J].电波科学学报,2007,22(4):571-576.YUAN Zhi-yong,LI Tun,CHEN Shui-ming,et al.Design and calibration of reverberation chamber[J].Chinese Journal of Radio Science,2007,22(4):571-576.(in Chinese)

[6] Geoffroy Lerosey,Julien de Rosny.Scattering cross section measurement in reverberation chamber[J].IEEE Transactions on Electromagnetic Compatibility,2007,49(2):280-284.

[7] Stephanie Mengue,Elodie R ichalot,Odile Picon.Comparison between different criteria for evaluating reverberation chamber functioning using a3-DFDTD Algorithm[J].IEEE Transactions on Electromagnetic Compatibility,2008,50(2):237-245.

[8] YUAN Zhi-yong,HE Jin-liang,CHEN Shui-ming,et al.E-valuation of Transmit Antenna Position in Reverberation Chamber[J].IEEE Transactions on Electromagnetic Compatibility,2007,49(1):86-93.

[9] Avila S L,SantosM A,Weinzierl D,et al.Maximum Working Volume Evaluation in a Non-Canonical Reverberation Chamber[J].IEEE Transactions on Electromagnetic Compatibility,2009,45(3):1646-1649.

[10] IEC61000-4-21,Testing and measurement techniques-Reverberation Chamber Test Methods[S].

[11] 王小平,曹立明.遗传算法理论、应用软件实现[M].西安:西安交通大学出版社,2002.WANG Xiao-ping,CAO Li-ming.Genetic Algorithm:Theory,Application and Software Implementation[M].Xi′an:Xi′an Jiaotong University Press,2002.(in Chinese)