基于ADRC的发电机励磁系统控制研究
2010-03-19李天云王雪奇
李天云 安 博 戚 为 王雪奇
(1.东北电力大学,吉林 吉林 132012;2.浙江省宁波鄞州供电局,浙江 宁波 315103)
1 引言
由于电力系统是强非线性、时变系统,而励磁控制在维持电力系统稳定中占有重要的地位,近年来发电机的非线性励磁控制方式的研究获得了飞速发展,并取得了丰硕的成果[1-4]。但是各种方法也各自存在不足:模糊PID等智能控制方法计算量大、控制很难满足实时性要求;自适应控制对有纯滞后、需要前馈补偿且动态过程变化缓慢的系统,可做到效果较好,但对动态过程变化迅速的系统效果欠佳,并且还存在稳定性、鲁棒性问题;H∞控制、变结构控制、鲁棒控制等理论尚未完全成熟,数学工具抽象、复杂,应用和推广受到影响。尤其是在实际发电厂中存在模型本身的参数扰动和测量装置的误差等,这些扰动通过各种途径进入励磁控制系统的测量环节,经综合放大单元放大,将严重影响系统的控制精度[5]。因此,寻找一种算法简单、抗干扰能力强、系统响应快、鲁棒性好、易于在实际现场中应用的励磁控制方法成为提高电力系统稳定性的关键。
本文将自抗扰控制技术[6]用于发电机励磁控制系统中,该控制技术是在继承传统PID不依赖于对象模型优点的基础上,通过改进传统PID固有缺陷而形成的新型控制器。它不依赖于系统的精确模型,将模型内扰(模型及参数的摄动)和不可测外扰的作用归结为系统的总扰动,利用非线性误差反馈的方法对其进行实时估计并给予补偿,控制对象参数发生变化或遇到不确定性扰动时都能得到很好的控制效果,具有较强的适应性、鲁棒性和可操作性。在非线性强的电力系统中更显出了其高速高精度控制的优越性。
2 自抗扰控制技术(ADRC)基本原理
2.1 ADRC的基本组成
自抗扰控制器由非线性跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制律(NLSEF)3部分组成,其二阶结构[9]如图1所示。
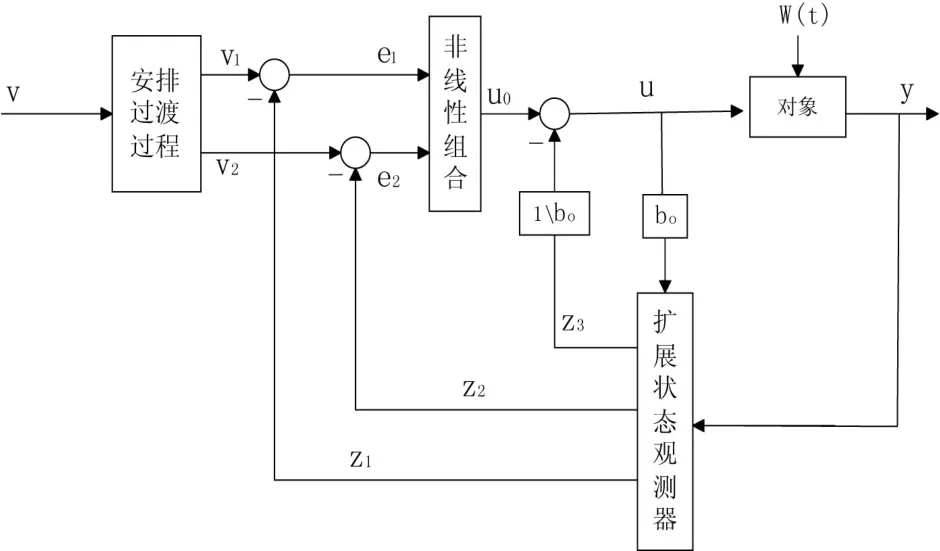
图1 ADRC结构图
2.2 ADRC各部分主要功能
(1)用跟踪微分器来安排过渡过程并提取其微分信号[7]。
(2)用扩张状态观测器来估计被控对象状态和不确定扰动因素,将含未知干扰的非线性不确定性对象化为积分串联型对象进行控制,系统的“模型”和“外扰”处于同等地位,都可以用ESO估计出其实时作用量而给以“补偿”。
(3)由安排的过渡过程与状态估计之间误差的非线性组合以及扰动估计的补偿来生成控制信号,非线性反馈控制律用一个简单的非线性函数实现了对控制工程界的经验知识“大误差小增益,小误差大增益”的数学拟合,提高了自抗扰控制器的动态性能和鲁棒性。
2.3 具有扰动跟踪补偿能力的二阶ADRC的具体实现算法
对于这样一类含有未知扰动w(t)的不确定对象
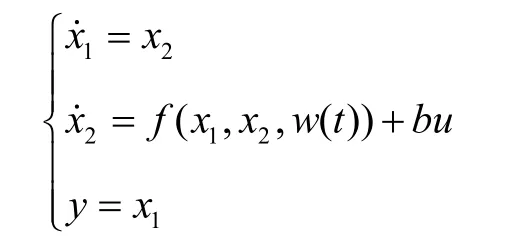
(1)设定v0为输入,用跟踪微分器(TD)安排过渡过程
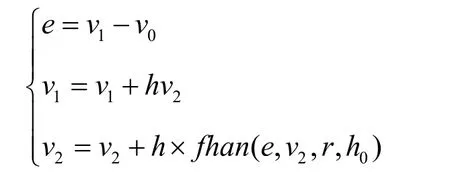
其中,v1为v0的跟踪信号,v2可视为v0的导数,h 是积分步长,h0为滤波因子。
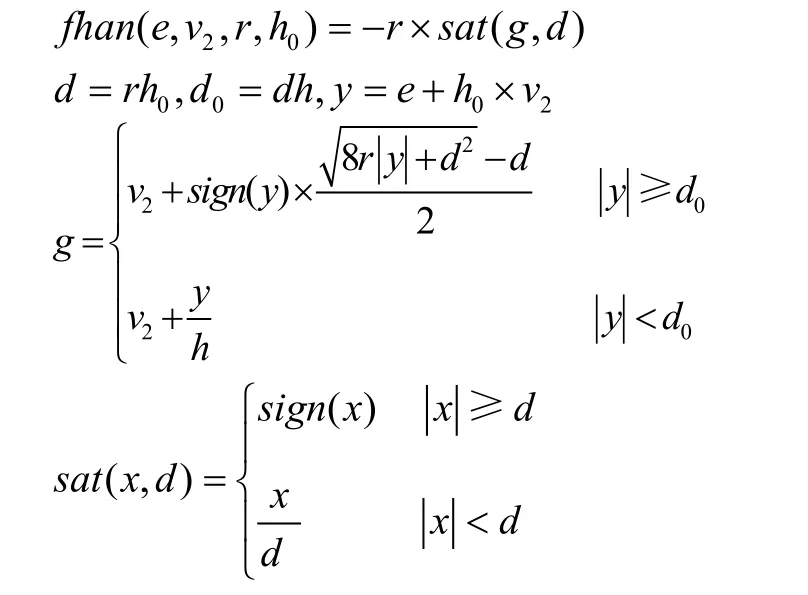
一般的控制系统中,误差直接取成e=v0-y,误差的这种取法使初始误差很大,易引起“超调”,很不合理。根据对象承受能力,若先安排合理过渡过程v1( t),然后误差取成e=v1( t)-v0( t ),就可以解决常规PID控制系统的“快速性”和“超调性”之间的矛盾,并提高调节器“鲁棒性”[6]。
TD的跟踪效果及滤波性能仿真研究:
1)输入信号v0( t)=cos(t)时,仿真波形如图2所示。
2)v0( t)=cos(t)+0.1rand(1)时,仿真波形如图3所示。
3)跟踪误差如图4所示。
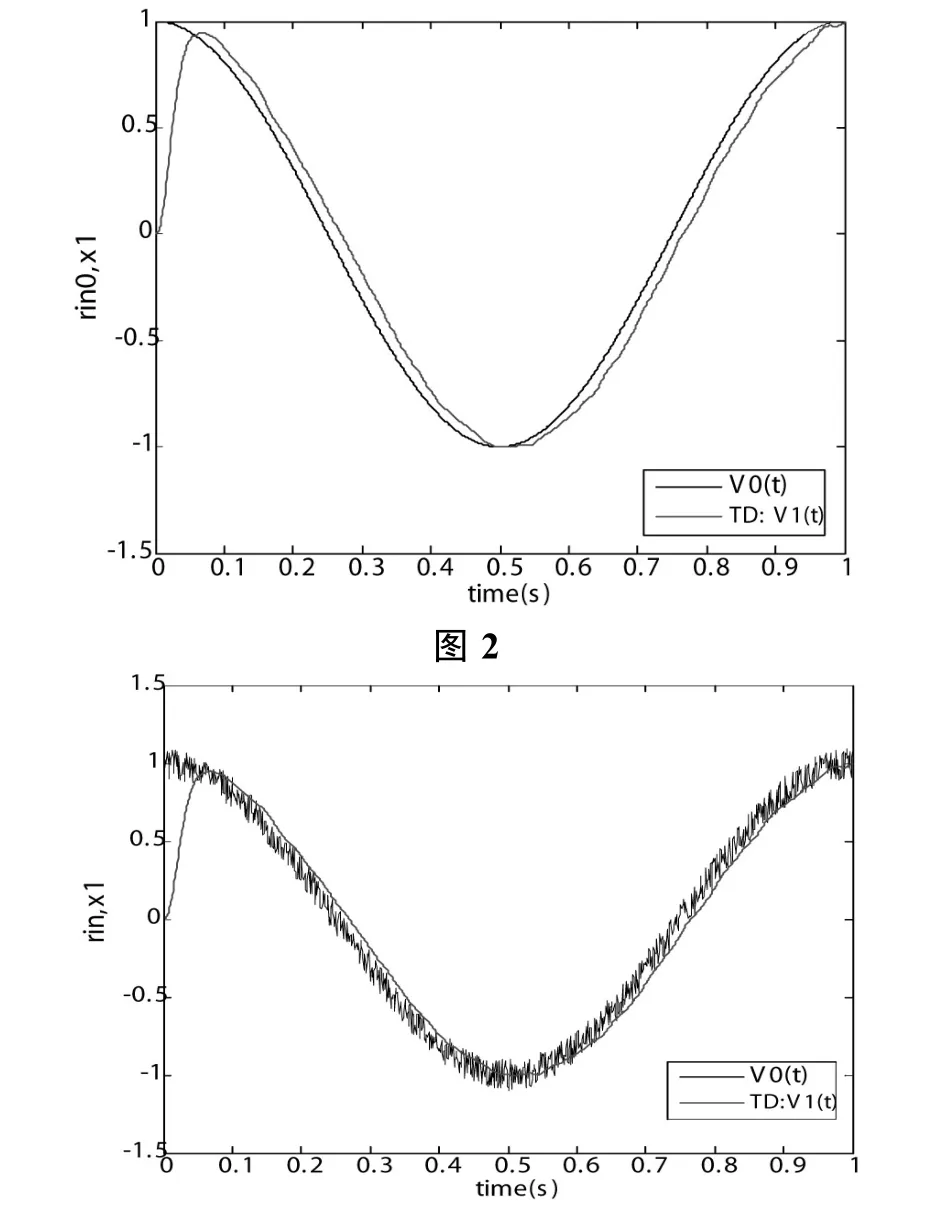
图3
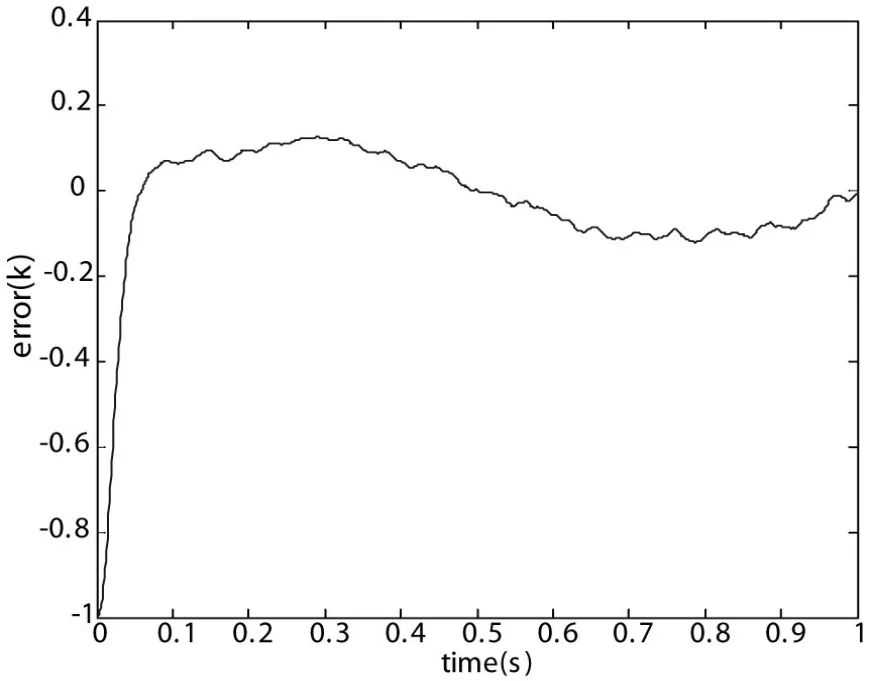
图4
由以上仿真可知:TD具有很好的滤波效果和快速跟踪能力。经仿真分析得出:r是决定跟踪快慢的参数。r越大,v1更快地跟踪信号v0,但当v0被噪声污染时,会使信号v1被更大的噪声所污染。为了滤掉v1所含的噪声,选取适当的h0,能获得很好的滤波效果。
(2)以系统输出y和输入u建立扩张状态观测器(ESO)来跟踪估计系统状态和扰动

文献[9]给出了自抗扰控制技术用于滤波的研究结果,提供了一些仿真实例。结果表明,这种新型的控制技术对高频噪声具有较好的滤波特性。并通过应用实例与卡尔曼滤波相比, 显示了其优越性和实用性。
3 发电机励磁系统的自抗扰控制律设计
图5为本文设计的存在模型参数扰动和量测误差扰动的发电机励磁系统方框简图,其中w为发电机的内部参数扰动,v为量测误差扰动。
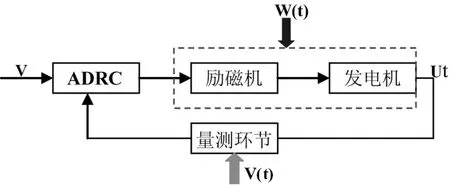
图5 励磁控制系统数学模型
若只研究励磁系统动态特性,且不考虑辅助控制信号,则励磁系统为单输入单输出系统,可以采用简化的传递函数来表征系统各个组成部分的数学模型[10]。
(1)同步发电机传递函数
只研究励磁系统的动态特性时,同步发电机的传递函数可以简化为一阶滞后环节
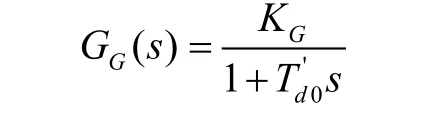
其中,KG为发电机的放大系数,为其时间常数,忽略发电机的磁场饱和现象。
(2)移相触发单元及功率单元传递函数
经简化处理,此单元用一阶惯性环节来表示
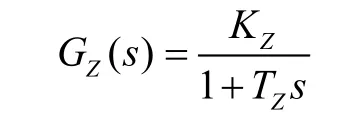
(3)电压测量环节传递函数
电压测量环节由测量变压器、整流滤波电路及测量比较电路组成。其中整流滤波电路略有延时,可用一阶惯性环节来近似描述。其它电路一般可忽略它们的延时。因此,电压测量的传递函数可表示为
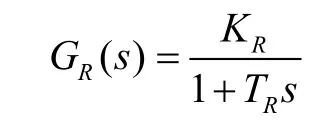
这样得到了被控对象的控制模型。以机端电压为控制目标,整个发电机励磁系统可以采用二阶跟踪微分器,三阶扩张状态观测器对励磁系统进行自抗扰控制律设计。
4 仿真及结果分析
本文采用Matlab/Simulink仿真工具对基于ADRC的励磁控制系统进行仿真试验,搭建仿真图如图6所示。分别考虑了发电机励磁系统分别受到突变扰动、模型扰动和测量误差等随机扰动时机端电压的影响,并与经典PID的控制效果进行了比较。其中励磁控制系统各部分参数选为:发电机转子时间常数=6.148s ,K=1.0;功率单元T=0.3s,K=1.0;GzZ电压测量环节TR=0.02s,KR=1.0。控制律中δ=0.01,k1=20,k2=2。
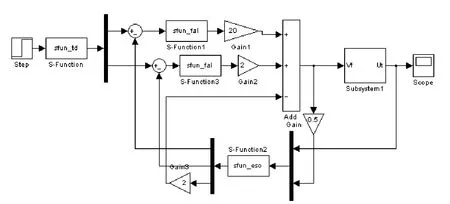
图6
(1)在仿真进行2s时突加幅值为0.1,持续时间0.2s的方波扰动[11],机端电压响应如图7所示。
(2)将励磁系统加入方差为0.001的白噪声w(t)作为系统模型随机扰动时,机端电压响应如图8所示。
(3)将电压测量环节加入方差为0.001的白噪声v(t)作为系统模型随机测量误差时,机端电压响应如图9所示。
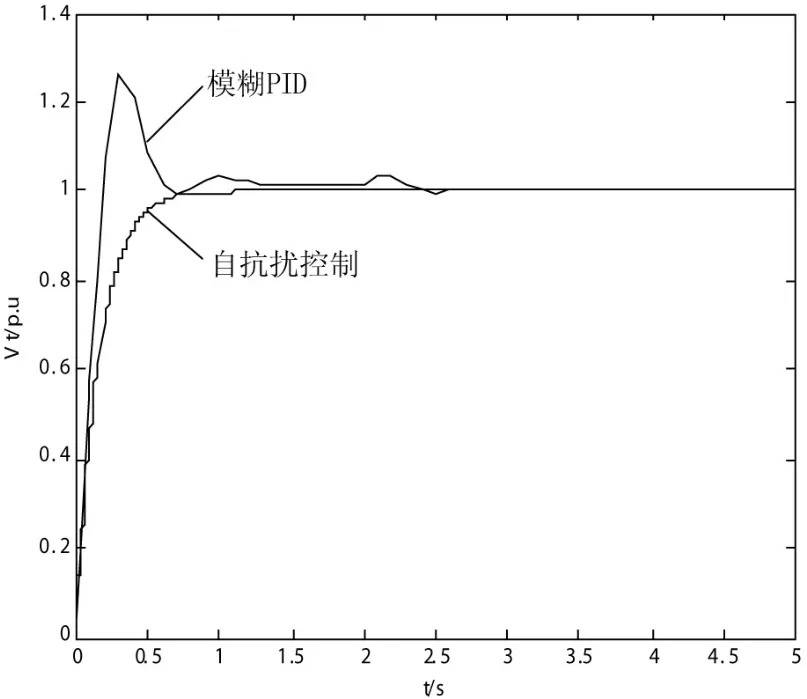
图7 2s时加入5%阶跃扰动机端电压响应曲线
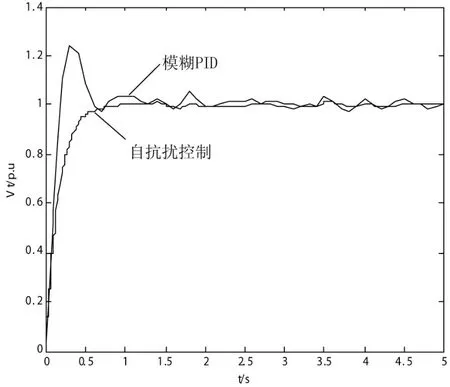
图8 w(t)下机端电压响应曲线
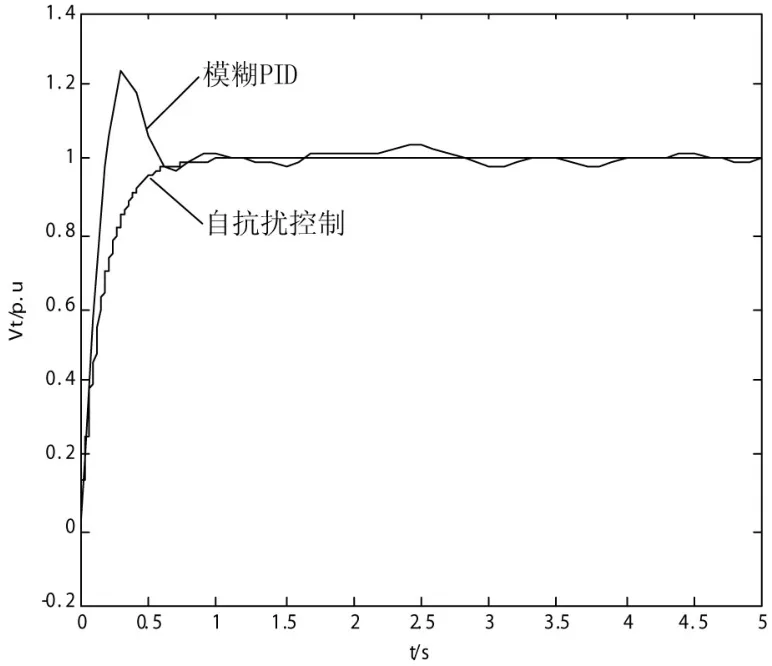
图9 v(t)下机端电压响应曲线
由以上仿真图形分析可知,基于自抗扰控制技术所控制的机端电压几乎不受到各种随机干扰的影响,比经典PID励磁控制具有更好的鲁棒性,从而有效改善了机端电压的控制精度,并且系统响应快,超调小。
5 结论
基于自抗扰控制技术的励磁系统控制策略对系统中存在的各种不确定扰动具有很好的适应性和鲁棒性,有效地提高了机端电压的控制精度,从而使电力系统的稳、准、快的性能指标都得到了改善。该控制方法算法简单,控制效果好,是一种易于在实际现场中应用的励磁控制方式。
[1] 万黎,邓长虹,陈允平.考虑机端电压限制的多重非线性变结构励磁控制[J].电机工程学报,2008,28(19): 86-92.
[2] 金岫,邓志良,张鸿鸣. 基于模糊PID控制的同步发电机励磁控制系统仿真研究[J].继电器,2007,35(19), 13-15.
[3] 何占宾.基于微分几何理论的发电机非线性励磁控制的研究[D].华北电力大学硕士论文,2007.12.
[4] 刘辉,李啸骢,韦化.基于目标全息反馈法的发电机非线性励磁控制设计[J].电机工程学报,2007,27(1),14-18.
[5] 刘海燕.计及随机干扰的同步发电机自动励磁控制系统的研究[D].华北电力大学硕士论文,2005.12.
[6] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008:243-264.
[7] 黄焕袍,武利强,高峰等.自抗扰控制在火电厂主汽温控制中的应用[J].系统仿真学报,2005,17(1),241-244.
[8] 武利强,林浩,韩京清.跟踪微分器滤波性能研究[J].系统仿真学报,2004,16(4):651-652.
[9] 宋金来,甘作新,韩京清. 自抗扰控制技术滤波特性的研究[J].控制与决策,2003,18(1):110-112.
[10] 孙新志.基于遗传算法的同步发电机模糊PID励磁控制器研究[D].西安理工大学硕士论文,2005.
[11] 揭海宝,郭清滔,康积涛等.基于模糊自调整PID控制的同步发电机励磁研究[J].电力系统保护与控制,2009,37(9):92.
