基于TD-LMS算法的OFDMA上行链路载波频率偏移消除*

关庆阳 赵洪林 郭庆

(哈尔滨工业大学通信研究所,黑龙江哈尔滨 150001)

作为未来通信的多址接入技术,正交频分多址接入(OFDMA)技术已经得到更广泛的应用.由于正交频分复用(OFDM)的子载波的正交性为多用户的接入提供了更便利的条件,来自不同用户的传输信息在时域内占用互相重叠的子载波,因而,OFDMA系统被IEEE 802.16E选为多址接入技术的物理层标准之一[1].与OFDM系统相比,OFDMA系统对子载波频率偏移更为敏感,OFDMA系统需要更多的子载波和更窄的载波间隔,同时每个接入用户的子载波都有不同的频率偏移[2],因而导致整个系统的干扰消除更为困难.与OFDMA下行链路相比,多用户频率偏移对上行链路的影响更大些[3].为克服这种多载波频率偏移的影响,最小二乘法(LS)被提出[4],但是其需要获知频率偏移的先验知识.Huang等[5]提出一种频域循环卷积方法,在接收端进行载波频率偏移(CFO)补偿以及多用户消除,但是这种算法仅限于载波频率偏移的波动间隔很大的情况下,补偿效果较好.文献[6]提出一种SAGE(Space-Alternating Generalized Expectation-Maximization)算法来消除OFDMA上行链路非同步引入的干扰,但是算法的复杂度高.文献[7]提出最大似然估计算法来进行干扰估计,虽然降低了复杂度,但是难以实现.文献[8]提出最小均方误差(MMSE)均衡算法来消除上行链路干扰,但是随着子载波数目的增大,算法的复杂度也增加.文献[9]指出串行干扰消除方法(SIC)的性能与干扰消除顺序有关.文献[10]提出按照功率大小进行子载波排序,然后采用基于最小均方准则的串行干扰消除算法(MMSE-SIC)消除频率偏移干扰.文献[11]提出按照信干比顺序进行子载波排序.文献[9-11]提出的SIC算法受第一级判决的约束,如果第一级判决错误,积累的判决误差将引起后面各级性能的下降,严重降低整个系统的性能.

文中提出一种时域自适应最小均方误差算法(TD-LMS)在时域内消除载波频率偏移引起的干扰.首先对接收的频率偏移信号进行预估计,利用估计量对频率偏移值进行调整,然后采用TD-LMS算法在时域内消除残留频率偏移的干扰.

1 系统模型

假设OFDMA系统上行链路共有T个用户与基站进行通信;并且每个用户已经预先被分配了特定的子载波.用户i共有N个子载波,用户i所发送的一个数据帧的信息为Xi(0),Xi(1),…,Xi(N-1),然后通过反傅里叶变换调制送上各自独立的子信道.发送前,需要在每个数据帧前添加循环前缀形成保护间隔来防止信道干扰.设M(i)表示用户i对子载波的占用情况,如果用户i占用了第k个子载波,此时M(i)可以表示为M(i)(k,k)=1.用户i发送的第n个信号经调制可以表示为

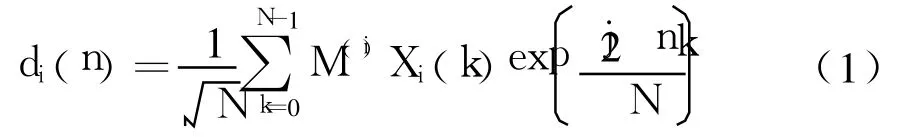
用户i信号经过信道后可以表示为

式中:*表示线性卷积;hi(n)为用户i的信道响应.引入频率偏移后,用户i的时域信号为

式中:ξi为用户i引入的载波频率偏移;g(n)表示均值为零,方差为 σ2的加性高斯白噪声.将接收的所有用户信号y(n)进行离散傅里叶变换(DFT)解调后可得

式中:Si(k)为用户i接收信号的频域表示;G(k)为高斯白噪声的频域表示;P(ξi)为频率偏移引起用户i的频域N×N干扰矩阵,可以表示为

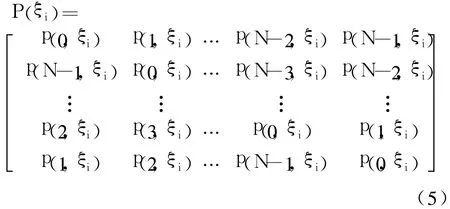
矩阵元素p(l,ξi)可以表示为

式中:l为子载波索引号的间隔距离.令m表示用户i中除载波k外的其余载波,u表示OFDMA系统中用户j占用的子载波,其载波数设为θ,则pj(u-k,ξj)为用户j的由载波频率偏移引起的对用户i的干扰,将频率偏移引入的干扰分离出来,式(4)可化简为

公式(7)第1项表示用户i接收的无载波干扰信号,第2项表示用户i中,除载波k外的其余载波m的干扰,即载波间干扰,第 3项表示用户 j的所有载波对用户i的多址接入干扰,第 4项为加性高斯白噪声的频域表示.而文中所采用的TD-LMS算法就是在时域内,降低频率偏移ξi对OFDMA系统上行链路的影响.

2 OFDMA上行链路频率偏移消除

为实现OFDMA上行链路载波频率偏移的消除,首先在时域内对带频率偏移的信号进行估计,并采用估计量对载波频率偏移值进行预消除,然后通过TD-LMS算法消除系统残留载波频率偏移的干扰.这是因为TD-LMS算法直接处理较大的频率偏移干扰时,性能有限,所以需要在前端进行频率偏移干扰预消除,以提高消除性能.

2.1 频率偏移时域估计及预消除

令频率偏移的均值 ¯ζ为用户 i频率偏移 ξi的估计值,r(n)为对应于yi(n)、收发端已知的无频率偏移理想信号,令其所占用的载波数为L,并且L≪N.利用已知信号r(n)进行频率偏移粗估计及预消除,同时可以将已知信号作为参考信号来完成TD-LMS算法的自适应学习.由此,频率偏移可以表示为:

公式(3)代入公式(10)后,可得

式中:ρi为预消除频率偏移后的残留频率偏移,满足.后端采用的时域TD-LMS算法就是对残留频率偏移ρi进行自适应消除.

2.2 用TD-LMS算法消除残留频率偏移

经预消除后,残留频率偏移 ρi数值较小,可以通过时域自适应TD-LMS算法消除,具体的消除过程如图1所示.

图1 TD-LMS算法频率偏移消除原理Fig.1 Elimination principle for frequency offset with TD-LMS algorithm

TD-LMS算法的消除过程如下:载波频率偏移预消除后,带有残留频率偏移ρi,将信号zi(n)作为TD-LMS滤波器的输入,x(n)为经过TD-LMS算法处理后的输出信号.当n≤L时,r(n)作为收发端预先共知的参考信号,经过自适应学习,TD-LMS算法达到收敛状态;当L＜n＜N-1时,滤波器判决后的输出信号r(n)作为参考信号来完成对剩余偏差信号zi(n)的消除.定义时域代价函数为

式中:E为对信号求期望值运算,H表示向量的共轭转置.代价函数对权值向量w(n)求梯度可得

经运算可得

式中:ΔJ(n)为代价函数的梯度表示;Rz,z(n)为接收的第n个时域信号的自相关函数,Rz,z(n)=E[zi(n)◦zi(n)];Rz,r为接收第n个时域信号与参考信号的互相关函数,Rz,r=E[zi(n)rH(n)].通过权值向量的递推关系可以得到

式中:μ为自适应步长.更新权值向量,可以得到

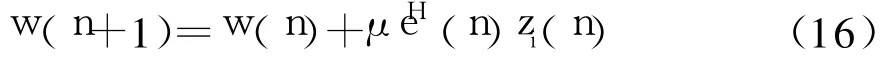
将频率偏移干扰代入公式(16),误差信号e(n)可以表示为

并且

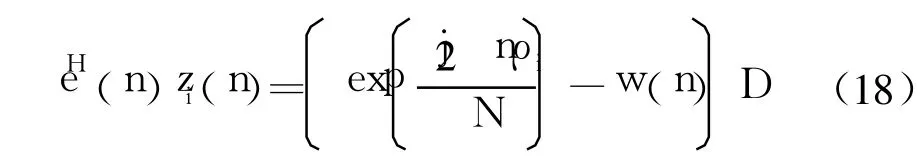
式中:D为信号向量经运算后得到的实常数,D= r(n)rH(n).

更新权值矩阵w(n),可以得到

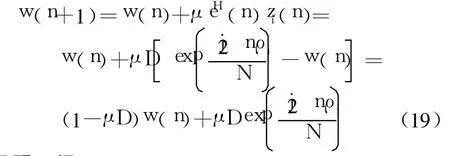
取极限可得

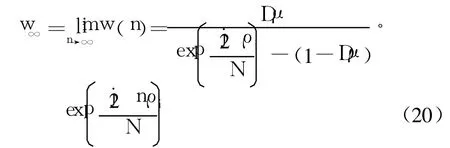
输出信号可以表示为

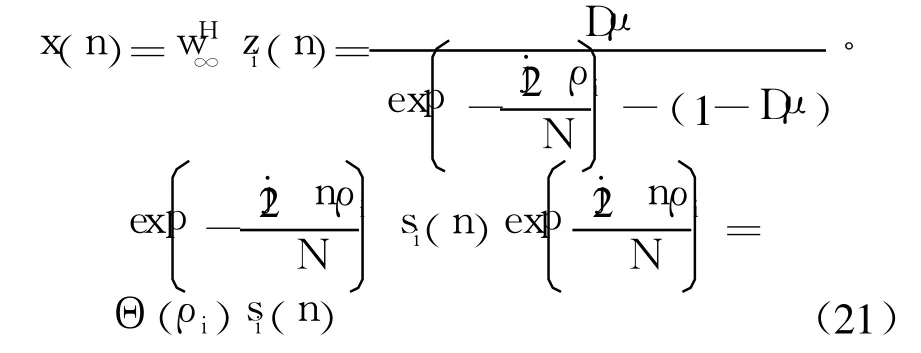
式中:Θ(ρi)为算法消除后的干扰因子.从公式(21)可得,TD-LMS算法可以获得将带有频率偏移的信号zi(n)与消除乘积的效果,并且可以提取出无频率偏移干扰理想信号si(n);事实上,当ρi≠0时, Θ(ρi)乘积因子会改变TD-LMS算法的输出幅度,并会带来固定相位旋转.由于TD-LMS算法所针对的是经过预消除后的残留频率偏移,频率偏移值很小,所以幅度以及相位影响可以忽略.

3 仿真结果及分析

3.1 仿真条件

采用Matlab软件验证文中提出的TD-LMS算法.假定OFDMA上行链路系统的子载波总数为256,用户数为 4,DFT窗口为 256,传输带宽设定为30MHz.设定每个用户都有独立的子信道,基带信号映射方式为正交相移键控(QPSK),频率偏移的范围设定为均匀分布,令分布范围为(-ξmax,ξmax),这里ξmax是每个子用户的最大频率偏移范围.

3.2 星座图仿真

通过对星座图的描绘能更加直观地看到 TD-LMS算法载波频率偏移的消除能力.本研究所采用的映射方式为QPSK.为了更清晰地看出基带信号星座图的变化情况,令信噪比SNR=10dB,取每数据帧OFDM数据符号为2000个,并且设单用户的固定频率偏移值为 0.15,图2示出了带有载波频率偏移的子载波信号星座图和经过TD-LMS算法消除后的子载波信号星座图.从星座图可以清晰看到TD-LMS算法能够消除由于频率偏移所引入的干扰.

3.3 误码率分析

图3示出了对于所有用户,ξmax=0.1,0.2,在不同信噪比下的平均误码率曲线,这包括无频率偏移干扰的情况、频率偏移干扰无消除的情况、文献[8]提出的MMSE修正算法、文献[4]提出的LS修正算法以及文中提出的TD-LMS自适应消除算法.本次仿真所采用的自适应TD-LMS算法的步长μ=0.075,权矩阵w取单位矩阵.图 3的条件是假定各子信道都是独立的.从图3中的曲线可以看到,与存在频率偏移干扰的情况相比,MMSE算法在一定程度上抑制加性白噪声的干扰,性能优于LS算法,文中提出的TD-LMS算法对频率偏移消除的误码率性能明显提高,对由载波频率偏移引起的多用户干扰消除效果明显.当ξmax= 0.2时,与LS算法相比,文中提出的TD-LMS算法在相同的误码率条件下,平均可获得3dB的增益.但是随着频率偏移范围的扩大,文中提出的算法的曲线与理论上的无频率偏移干扰的曲线偏离较大,这主要是由于较大的载波频率偏移范围引起了干扰波动.

图3 载波频率偏移分布于(-0.1,0.1)、(-0.2,0.2)时的平均信噪比的误码率曲线Fig.3 Bit-error-rate curves under different average signal-tonoise ratio when carrier frequency offset distributing in (-0.1,0.1),(-0.2,0.2)

3.4 TD-LMS算法自适应学习曲线

图4 TD-LMS算法自适应学习曲线Fig.4 Adaptive learning curves for TD-LMS algorithm

采用TD-LMS算法的均方误差的学习曲线见图4.从图 4中可以看出,经过一些数据包的加权运算,均方误差明显减小,而且经过 130个数据包的学习,均方误差可以降低到 10-4,这也可以证明TDLMS算法在时域内可以完成对OFDMA系统频率偏移的消除.

4 结语

文中提出了一种基于时域自适应TD-LMS算法的补偿方案来消除OFDMA上行链路的各载波频率偏移引起的干扰,TD-LMS算法自适应学习的能力较强,结合时域频率偏移估计及预消除过程,可以自适应地有效消除不同载波频率偏移引起的干扰.仿真结果表明,该补偿算法对由载波频率偏移引起的干扰补偿效果明显.

[1] The Institute of Electrical and Electronics Engineering. IEEE 802.16E-2005.IEEE standard for local and metropolitan area networks part 16:air interface for fixed and mobile broadband wireless access systems amendment 2: physicaland medium access control layers for combined fixed and mobile operation in licensed bands[S].New York:The Institute of Electrical and Electronics Engineering,2005:126-129.

[2] Morelli M.Tim ing and frequency synchronization for the uplink of an OFDMA system[J].IEEE Transactions on Communications,2004,52(2):296-306.

[3] Kivanc D,Li Guoqing,Liu Hui.Computationally efficient bandwidth allocation and power control for OFDMA[J]. IEEE Transactions on Wireless Communications,2003,2 (6):1150-1158.

[4] Cao Zhongren,TureliU,Yao Yu-dong.Analysis of two receiver schemes for interleaved OFDMA uplink[C]∥Signals,Systems and Computers,Conference Record of the Thirty-Sixth Asilomar Conference.Asilomar:IEEE,2002: 1818-1821.

[5] Huang D,Letaief K B.An interference cancellation scheme for carrier frequency offsets correction in OFDMA systems[J].IEEE Transactions on Communications, 2005,53(7):1155-1165.

[6] Lee Jong-ho,Kim Seong-cheol.Time and frequency synchronization for OFDMA uplink system using the SAGE algorithm[J].IEEE Transactions on W ireless Communications,2007,6(4):1176-1181.

[7] Pun O,Morelli M,Kuo J.Maximum-likelihood synchronization and channel estimation for OFDMA uplink transmissions[J].IEEE Transactions on Communications, 2006,54(4):726-736.

[8] Cao Zhongren,Tureli U,Yao Yu-dong,et al.Frequency synchronization for generalized OFDMA uplink[C]∥Global Telecommunications Conference,2004.Dallas: IEEE,2004:1071-1075.

[9] Trajkovic V D,Rapajic P B,Kennedy R A.Adaptive ordering for imperfect successive decision feedback multiuser detection[J].IEEE Transactions on Communications, 2008,56(2):173-176.

[10] Tevfik Y,Huseyin A.Carrier frequency offset compensation with successive cancellation in uplink OFDMA systems[J].IEEE Transactions on Wireless Communications,2007,6(10):3546-3551.

[11] Hou Shengwei,Ko CC.Intercarrier interference supp ression for OFDMA up link in time and frequency selective Rayleigh fading channels[C]∥VTC Spring 2008.Hannover:IEEE,2008:1438-1442.