基于小波域的二维混沌加密算法

龚岩琳，陈善学，徐皓淋

(重庆邮电大学 通信学院，重庆400065)

随着计算机网络多媒体技术和现代电子商务的发展，在机要、军事、政府、金融和私人通信中，数字图像所占的比例越来越大，它所承载的信息安全成为当前人们关心的焦点。保护图像信息安全,经济有效的方法是密码技术。但是传统的加密算法(如DES、RSA算法),虽然应用广泛，但其相应的破译方法已曾出不穷，更重要的是传统的加密算法并不适用于对图像及视频的处理。图像信息安全问题有着极为广泛的含义，考虑其安全算法时，必须考虑其数据的冗余性、对大数据量数据加密的可实现性及能否经受住常见的数据有损压缩、格式变换等操作。混沌动力学系统具有伪随机性、确定性和对初始条件与系统参数的极端敏感性，因此，它为图像信息加密提供了很好的途径，利用它可以构造非常好的信息加密系统。

基于图像变换域的算法是近年提出来的，主要采用的是离散余弦变换和离散小波变换。而基于离散小波变换域[1-2]的图像加密算法因为小波分析具有时域和频域的良好局部化性质而得到更加广泛的应用。对图像数据进行离散小波变换得到的小波系数矩阵，如果其中任何一个系数发生变化，就会引起图像原空间中的所有的像素点发生改变，如果将小波系数的变化看作一种加密方法，加密效果比只用混沌序列加密好得多。本文介绍的是在小波变换后的一种图像加密方法，该方法将二维混沌映射[3]应用于小波域来置乱图像，并且采用了位扩展的方法与混沌模板映射相结合的方法来达到更高的加密强度。针对该算法进行了相关的安全性能分析，实验结果表明，该算法具有良好的安全性。

l 混沌系统

1.1 一维Logistic序列[4]的混沌特性

混沌现象是在确定性非线性动力系统中出现的确定性、类随机的过程，这种过程没有明显的周期和对称，但是却具有丰富的内部层次的有序结构，并且对初始值有极其敏感的依赖性。Logistic映射是一种常见的混沌动力系统，基于一维Logistic映射进行加密是一种平凡的混沌加密，安全性难以保障，但可以证明二维Logistic映射所产生的混沌点集合不存在误差构造形式，具有更安全的加密效果。

Logistic映射是目前被广泛应用的一种混沌动力系统，其表达式为：

式(1)中，a成为分支参数，当 a∈(1.401 115...2]时，映射式(1)处于混沌状态，迭代得到在(0，1)上的伪随机序列

1.2 二维Logistic序列的混沌特性和统计特性

二维Logistic映射的系统模型为：

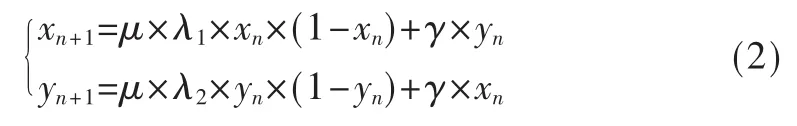
其中，x0、y0为系统初值，通常取值 x0=0.10，y0=0.11。 μ、λ1、λ2、γ为系统的控制参数，通常取μ=4。

1.3 加密模板

本文采用的加密模块为：

2 小波变换

采用双正交 9／7小波[5]作图像的二级小波分解，获得7个子带，从低到高分别为 LL2，HL2，LH2，HH2，HL1，LH1和HH1。图像子带特性有以下情况：LL2子带的能量大约占图像信号总能量的 95%； 第 2层(LL2、HL2、LH2、HH2、HL1)子带的能量大约占图像信号总能量的 97．5%；除LL2中的值基本是正值以外，其余各子带的值有正有负。本文算法根据变换域的图像能量的特点对LL2层系数进行位扩展的混沌置乱。二级小波的分解如图1所示。

3 加密／解密系统

3.1 加密过程

加密过程如图2所示。

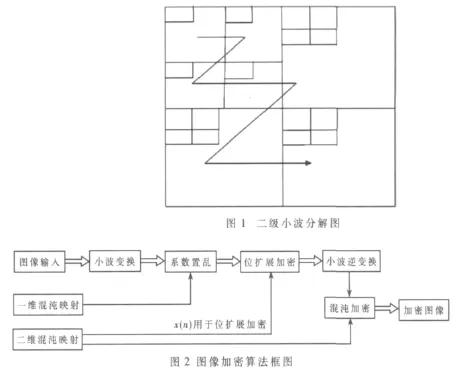
3.2 加密步骤

输入：原始图像、参数 1、参数 2、参数 3、参数 4、……。

输出：加密图像。

加密步聚如下：

(1)首先对大小为N×N的lena图像进行连续小波变换，本文采用的是二级bior3．7小波分解。

(2)根据输入的混沌参数由一维混沌映射开始迭代产生混沌序列，根据式(3)产生加密模板，并根据加密模板对二级小波分解后的各个系数进行调整。

(3)将调整后的小波系数分成低频部分(LL2)和高频部分(包括水平区域(HL2，HL1)、垂直区域(LH2，LH1)和 对角线组(HH2，HH1)3个部分)，选择低频系数进行位扩展[6]加密，根据输入的混沌参数由二维混沌序列生成序列x(n)和y(n)，其中 x(n)序列用来对低频部分进行位扩展加密，将x(n)从中间某位截断取大小为1/4×N×N个数，以 0.5为阈值对 x(n)进行二值化，得到一个 1/4×N×N大小的二值序列S,将二值序列 S中的第8×j位到8×j+7位的8个二进制位组成数据t(j),最后将t(j)与调整系数后的低频部分进行“异或”处理，即得到位扩展加密后的低频部分系数。

(4)对置乱后的小波低频系数和未进行处理的高频系数共同进行小波逆变换得到图像I，同时用二维混沌映射产生的大小为N×N的序列y(n)对图像 I进行置乱加密，得到最后的加密图像。

3.3 解密步骤

输入大小为N×N的待解密图像,二维混沌映射参数得到序列y(n)与待解密图像行进行“异或”处理，得到的图像进行二级bior3．7小波分解。将得到的小波系数的低频系数进行位扩展运算，将解密后的系数与其他的高频系数与混沌模板解密矩阵点乘,得到最后的小波系数。最后对小波系数进行小波逆变换,得到解密后的图像。

4 实验结果及分析

4.1 破解实验

在Matlab7.1编程环境下采用本文的算法对256×256的lena图像进行加密。其中a=1.831 5,一维混沌初值为0.410 35,二维混沌初值 x0=0.10，y0=0.11, μ=4,λ1=0.89，λ2=0.89，γ=0.1,Arnold置乱的迭代次数为 20,初值 a=15,b=7,实验结果如图3所示。图3(d)是用上述加密密钥相同的参数得到的正确解密图像，图3(e)是用x0=0.10，y0=0.11，μ=4，λ1=0.890 003 2，λ2=0.89，γ=0.1 的 参 数 进 行解密的图像，可见只是一个密钥小数点后的数值不一样，而其他密钥都正确，也得不到正确的解密图像，可见该加密算法具有密钥敏感性，不宜破解。

4.2 耗时测试

耗时测试实验目的是验证位扩展混沌算法的时效性。 Arnold 算法在图像尺寸为 128×128、256×256、512×512的周期依次为 96，192，384，分别设定密钥为 50、100、200；位扩展算法的密钥设为a=1.952，x0=0.143,则结果如表1所示。

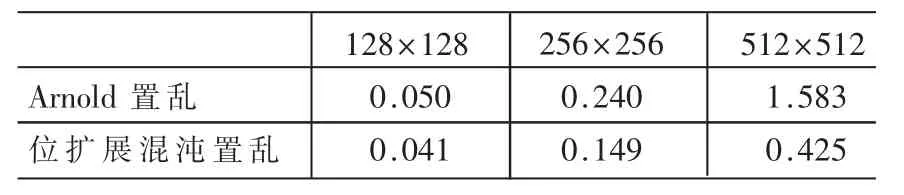
表1 算法耗时比较(单位：s)

由表1可知，基于为扩展的混沌算法在实效上优于Arnold算法，图像越大优势越明显。

4.3 压缩分析

在基于小波压缩域的加密技术中，目前主要两种方法为CWW和CWF。CWW指在整个图像N×N的范围内置乱，使得高频系数和低频系数产生迁移。若要进行编码或压缩处理时，低频到高频的系数迁移会造成量化误差，影响解码的质量，甚至会造成比特溢出而无法继续编码过程;而高频到低频的迁移，则会严重影响编码的效率。这种对整个小波系数的置乱方法对压缩的能力影响极大，会使得有损压缩无法进行。因此本文只在同一个频带内置乱则不会出现这种情况，使得本算法适合于压缩编码等情况。压缩处理过程只会造成解密图像质量的下降，不会对图像要表达的内容构成实质性损害。

本文将位扩展运算运用于小波域来加密图像，同时与混沌模板序列相结合，并利用二维混沌序列对图像的小波系数进行置乱和置换变换，实现了小波变换域的高强度加密。本文提出的算法不仅能获得很好的加密效果，而且相比于其他的置乱算法，可以很大程度地节约计算时间，减小计算的复杂度。同时采用混沌加密模板，比传统的混沌序列有更高的加密强度。密钥简单，但空间却很大，不易破解。仿真实验表明，该算法的实用性很强，在不改变小波系数值的前提下，运算速度快，加密造成的膨胀量小。

[1]胡蓉，王玲，罗卓伟.小波域图像加密的模运算实现[J].计算机工程与应用,2009,45(8):121-122.

[2]邱炳城，姚仰新，陈银冬.用小波变换和混沌映射实现图像置乱[J].计算机工程与应用,2009，45(11):102-103.

[3]邹建成，徐雅琴．一种基于二维Logistic混沌映射的数字图像加密算法[C]．2008世界通信大会中国论坛一网络和信息安全分论坛，2008.

[4]SCHARINGER J．Fast encryption of image datas using chaotic kolmogorocv flows[A]．Proceeding of the International Society for Optical Engineering[C].SanJose California，1997.

[5]穆国旺，张文华，陈雅颂．基于非交换小波变换的图像置乱算法[J]．计算机工程与应用，2006，42(35)：74-76．

[6]殷肖川，蒋晓迪，周翔翔.基于位扩展的灰度图像混沌加密算法[J].空军工程大学学报(自然科学版),2008(2):58-60.