基于分数阶傅里叶变换的多项式相位信号参数估计*
2010-03-15张天骐杜晓华
金 翔,张天骐,庞 统,杜晓华
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
多项式相位信号(PPS)是信号处理领域中一个具有重要意义的非平稳信号模型,它在雷达、声纳、语音和通信领域得到了广泛应用。LFM信号是PPS的一个特例,当前LFM信号参数估计方法主要通过二维目标函数结合二维搜索来实现,比如最大似然估计、基于时频分析的参数估计方法、FRFT、匹配傅里叶变换(DCFT)等。由于二维搜索法计算量较大,尤其当估计的精度要求较高时,浪费了大量时间去作对检测无用的变换计算。为了解决这些问题,本文研究了多项式相位信号估计的一种快速算法。
1 基于分数阶傅里叶变换的LFM信号检测与参数估计
信号 x(t)的 FRFT定义为[1]:

式中FRFT的变换核Kp(t,u)为:

其中,n为整数,α称为旋转角度,且 α=pπ/2,p为 FRFT的阶数,Fp[·]为 FRFT的算子符号。
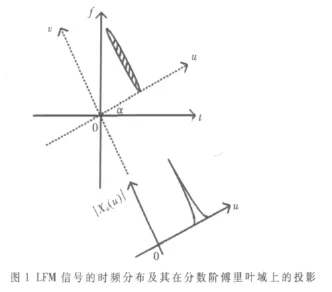
信号x(t)的FRFT是线性变换,它与WVD的关系可解释为时频平面的旋转算子,这一特性决定了FRFT特别适合于处理LFM类信号[7]。如图1所示,一个有限长LFM信号的Wigner分布在时频平面呈现为斜直线的背鳍形分布,因此,若在与该斜直线相垂直的分数阶域上求信号的分数阶Fourier变换,则在该域的某点将出现明显的峰值。而噪声的能量均匀地分布在整个时频平面内,在任何的分数阶Fourier域上均不会出现能量聚集。利用这一特性,可实现LFM信号的检测和参数估计。
设含有噪声的单分量LFM信号表示为:
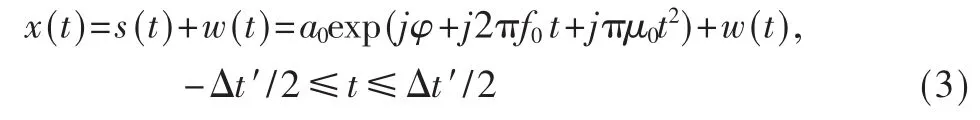
其中,a0、φ、f0和 μ0分别为信号幅度、初始相位、初始频率和调频斜率,w(t)为加性高斯白噪声(方差为σ2)。则上述的chirp信号检测和估计过程可描述为:
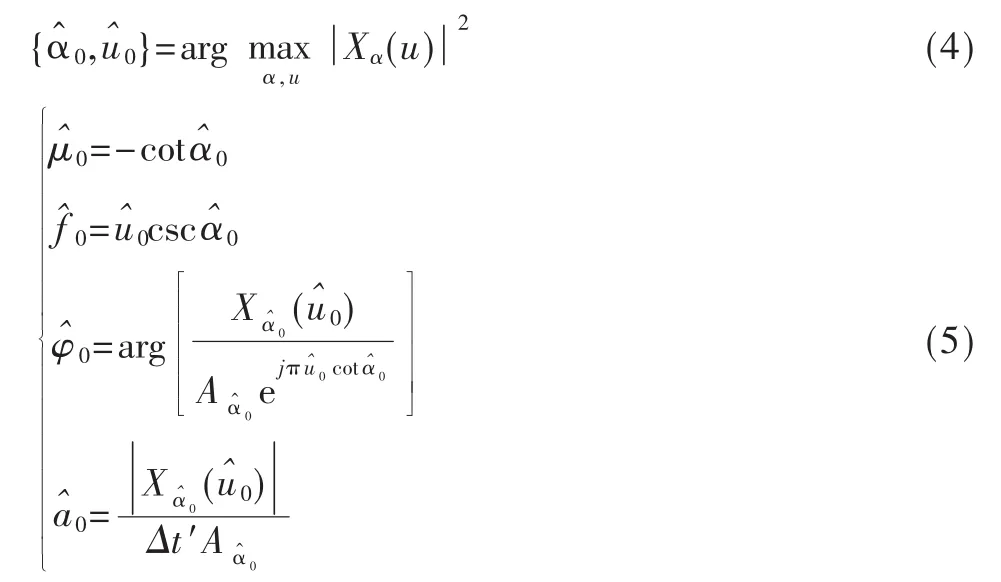
2 延时相关解调技术与FRFT的快速算法
2.1 LFM信号延时相关解调
设含有噪声的单分量LFM信号x(t)为:
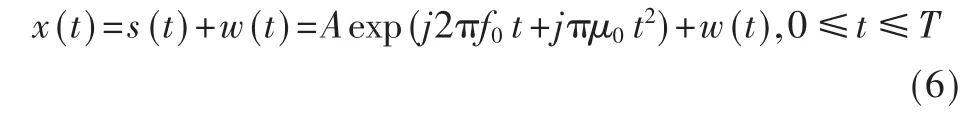
其中 A、f0、μ0分别是 LFM信号的幅度、初始频率、调频斜率,w(t)是零均值平稳高斯白噪声,方差为σ2。参考文献[3]证明了LFM信号经延时相关解调后变成一个频率为 f0′=μ0τ的正弦信号和均值为零的噪声信号,且方差为2A2σ2+σ4。
所以可以通过FFT估计该正弦信号频率 f0′,得到LFM信号参数μ0的估计值:

[2]论证了 τ的最佳选择在 τ=0.4T时,且调频斜率的搜索范围为[3]:
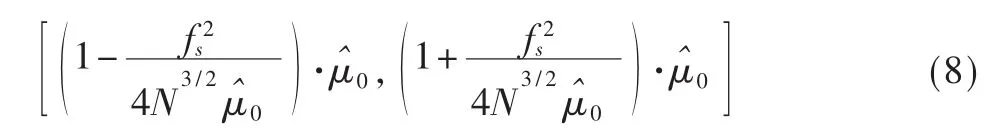
其中,N是采样点数,fs是采样率。
2.2 多项式相位信号延时相关解调
本文讨论非线性调频信号在雷达中的应用,只考虑三阶PPS信号的参数估计,信号的模型为:
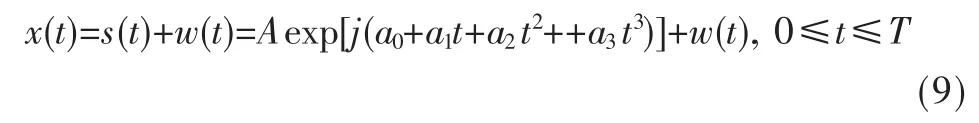
其中,A为信号幅值,w(t)是零均值平稳高斯白噪声,方差为σ2。一次延时相关解调可以使相位阶数下降一阶,现考虑二次延时相关解调。
参考文献[5]证明了PPS信号经二次延时相关解调后变成一个频率为 f0=6τ2a3/2π的正弦信号淹没在均值为0、方差为 6A6σ2+10A4σ4+4A2σ6+σ8的噪声中,即信号 x(t)经过二次延时相关解调后,接收信号延时相关函数的信噪比RSNRo与原始信号信噪比(RSNRi)的关系为:

通过FFT估计该正弦信号频率f0,就可以得到多项式相位信号参数a3的估计值:

参考文献[5]从正弦信号频率估计的角度,说明了τ取 2T/7 时,3的误差最小。
基于以上分析和PPS信号的性质,PPS(三阶)信号估计可按以下步骤进行:
(1)信号 x(t)通过二次延时相关解调,由式(11)估计出最高阶项系数3;
(2)构造参考函数 xr(t)=exp[j(a1t+a2t2++a3t3)]·exp(-ja3t3),对xr(t)作FRFT,由式(5)可进行相关参数的估计。
3 仿真实验与结果分析
实验一:设信号的数学模型如下式表示:
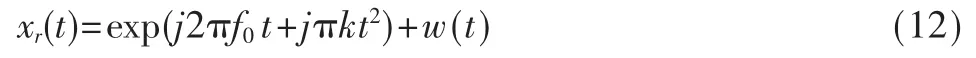
采样点数为1 024,采样频率fs=1 000 Hz,初始频率f0=345 Hz,调频斜率k=100,w(t)为高斯白噪声。 当信噪比为-2 dB时,若取分数阶的步长Vp=0.000 1进行FRFT,得到三维图如图2所示,进行能量的最佳搜索。由式(5)可估计出信号为:
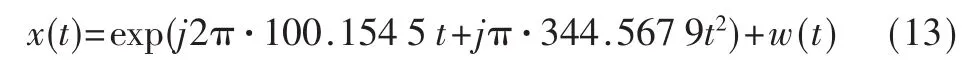
用延时相关解调方法得到正弦信号,然后对其作离散傅氏变换,如图3所示,由幅度谱可得到调频斜率k=90.609 4,代入相关参数到式(8),得到调频斜率k∈(91.980 0,107.238 8),从而得到分数阶p的搜索范围p∈(1.0597,1.0696)。

由此可以在相应区间进行FRFT,得到其对应模值,如图4所示,其横轴为分数阶p,纵轴为相应的p对应的模值,可以从图中得到p=1.065 0时,模值最大,即此时有最佳能量聚集特性。图5为最佳能量聚集时的分数阶模值图,从图中明显看出能量的聚集性。此时,估计出信号为:
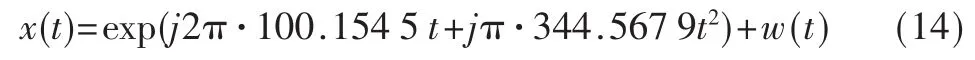


通过比较式(13)和式(14)可以看出两者结果一样,原因是两者旋转角度采用相同的步长,而采用相关解调后分数阶区间缩小到(1.059 7,1.069 6),在相同精度的条件下其计算量与二维搜索法计算量相比是其1/400以下。由于没有在时域附近做FRFT,所以不会出现伪峰干扰。
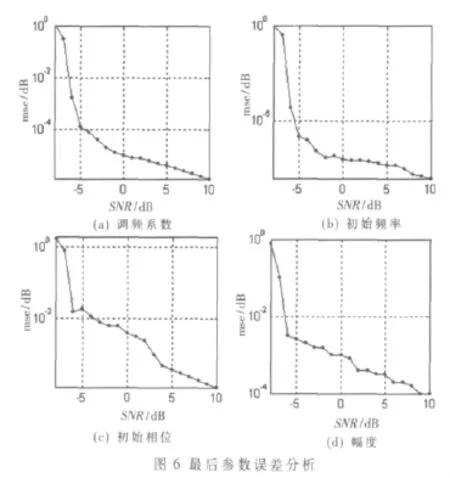
图6为LFM信号参数的误差分析图,从图中可以看出在信噪比大于-6 dB情况下,可以较为准确地估计出信号参数,由于最终信号各参数的估计值都是基于FRFT检测的,所以此种方法并不影响误差。
实验二:设信号的数学模型如下式所示:
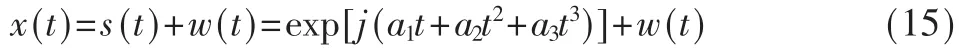
其中采样频率 fs=1 024,采样点 N=1 024,a1=20,a2=100,a3=50,t=2T/7。
x(t)信号相关解调后,输入 SNR范围为-4~6 dB,分别运行200次Monte Carlo实验,图7是采用此方法得到的均方误差随信噪比变化的特性图,从图中可以看出,当信号信噪比大于0 dB时,算法的性能比较稳定。
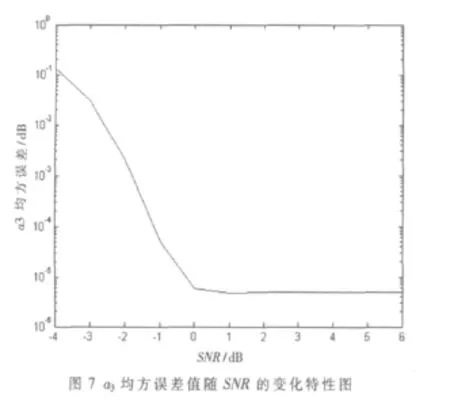
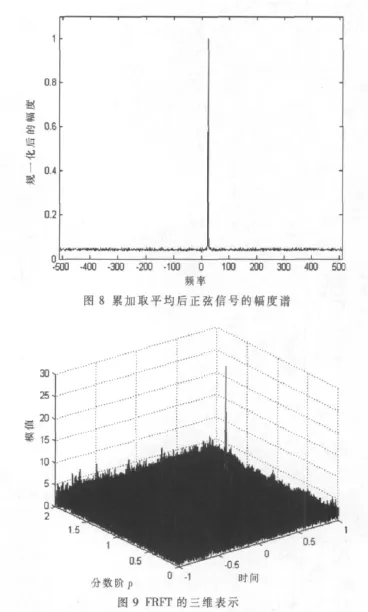
对于(12)式的信号模型,设 SNR=6 dB,由图 8正弦信号的幅度谱和式(11)可得到a3=50.265 5,再按多项式相位信号估计步骤进行估计,进行FRFT,得到三维图如图9所示。根据公式(5)估计出信号为:

目前对FRFT的计算简便方法的研究已经比较深入,通过分解法可使分数阶计算的量逼近于(NlogN)[1],由于计算量非常之大,本文提出了先延时相关解调,粗略估计LFM信号调频系数的范围,再进行小范围数值的分数阶变换,大大减小了计算量,变二维谱峰搜索为一维搜索,并且在信噪比大于-6 dB时,取得了较好的效果。同时,引入分数阶傅里叶变换与延时相关解调相结合,对多项式(三项式)相位信号进行检测,在信噪比大于0 dB时取得了较好的效果。
参考文献
[1]陶然,齐林,王越.分数阶 Fourier变换的原理与应用.北京:清华大学出版社,2004.
[2]刘渝.快速解线性调频技术[J].数据采集与处理,1999,14(2):175-178.
[3]冯小平,李晨阳.线性调频信号参数快速估计[J].系统工程与电子技术,2005,27(2):237-239.
[4]董永强,陶然,周思永,等.含末知参数的多分量chirp信号的分数阶傅里叶分析[J].北京理工大学学报,1999,19(5):612-616.
[5]靖晟,刘渝,席轶敏.非线性调频信号参数估计算法[J].南京航空航天大学学报,2001,33(5):411-444.
[6]NAMIAS V.Thefractional order fourier transform and its appliction to quantum mechanics.J.Inst.Math.App1.1980,25:241-265.
[7]DONG Yong Qiang,TAO Ran,ZHOU Si Yong,et a1.The fractional fourier analysis of multicomponent LFM signa1.Chinese Journal of Electronics,1999,8(3):326-329.
[8]齐林,陶然,周思永,等.基于分数阶Fourier变换的多分量LFM信号的检测和参数估计.中国科学E辑,2003,33(8):750-759.
[9]张希会,蔡竟业,杨亦师.基于分数阶傅里叶变换的LFM信号参数估计预判法[J].信号处理,2008,24(4):667-671.
[10]韩孟飞,王永庆,吴嗣亮,等.一种低信噪比下LFM信号参数快速估计算法[J].北京理工大学学报,2009,29(2):147-151.
