月壤特性对月球车轮地相互作用力的影响

邓宗全，丁 亮，高海波，陶建国，王少谦

(哈尔滨工业大学机器人技术及系统国家重点实验室，哈尔滨150080，liang.ding@hotmail.com)

中国“嫦娥”探月计划二期工程预计于2013年左右发射月球车进行月面巡视勘测.月球车轮地相互作用地面力学被广泛应用于探测车结构设计、性能评价、土壤参数辨识、动力学仿真、运动控制等方面，是目前的研究热点之一［1］.

轮地相互作用受到许多因素的影响.通过试验或者数值分析的手段，对于影响月球车等星球车轮地相互作用的车轮尺寸、轮刺分布、滑转和沉陷等现象等都进行了相关研究［2-6］，并且基于传统地面力学成果推导了月球车轮地作用力学模型［1，7］.月壤特性对于轮地相互作用力也存在显著影响，但是目前针对性研究成果并不多见.

由于月壤的物理和力学参数较多，制作不同的模拟月壤进行比较全面的试验研究是非常困难的.本文基于可以反映车轮滑转沉陷和轮刺效应的修正月球车轮地作用模型［1］，通过改变土壤特性参数，分析土壤特性对于轮地作用力的影响，为进行月球车轮力学性能预测和月壤参数辨识等应用提供依据.

1 月壤的物理和力学特性

1.1 月壤的物理特性

月球表面覆盖一层直径小于1 mm的细密粒子层(其中散布了很少的岩石块)，被称作风化层(regolith)［8］，这层风化层就是承载月球车的载体——月壤.下面对影响轮地相互作用力学的月壤物理特性进行介绍.

1)月壤的粒度分布.月壤的分选性较差，粒度与淤沙相似，但分布范围很宽，颗粒直径以小于1 mm为主，绝大部分颗粒直径在30 μm～1 mm，中值粒径在40 μm～130 μm，平均为70 μm［8］.

2)月壤密度ρ.Apollo月壤采样分析表明，月壤密度随着采样深度的增加而增加，密度与深度呈指数关系或双曲线关系，密度在 1.30 g/cm3～2.29 g/cm3.月球车与月壤的相互作用发生在表层，深度在0～15 mm的表层月壤，密度为1.45～1.55 g/cm3［9］.

3)月壤孔隙比e.孔隙比是指土壤中孔隙体积与颗粒体积之比，可以用来评价土壤的密实程度.一般e＜0.6的为密实土壤，e＞1.0的为疏松土壤.深度在0～15 mm的表层月壤孔隙比e为1.07±0.07［10］，因此月壤是比较松软的.

4)月壤的相对密实度Dr.密实度反映了土壤的承载能力，土壤密实度越大，其抗切强度越大，越难以产生压缩变形.Dr可用下式计算［11］:

根据文献中提供的月壤孔隙比、最大孔隙比和最小孔隙比［9-10］，代入式(1)进行计算，Apollo14～16和Apollo20采样月壤的相对密度分别为0.856，0.707，0.608和0.669.可见月壤的相对密实度比较大，因此其可压缩性比较小，车轮走过后月壤的变形也较小.

1.2 月壤的力学特性

应用地面力学研究土壤的力学特性时，通常借鉴Bekker半经验法的基本思想:将土壤的变形分解为相互独立的竖直方向变形和水平方向变形，分别对应于土壤的承压特性和剪切特性.

1.2.1 月壤的承压特性

土壤的承压特性非常复杂，目前，在研究汽车地面力学时多采用简化模型描述月壤的承压特性，其中Bekker承压模型的应用最为广泛.根据Bekker模型，土壤的平均压应力为［12］

式(2)是根据压板试验得到的经验公式，σ为压板下部平均法向应力，bp为压板实验中压板的短边长度或半径，kc为土壤内聚变形模量，kφ为摩擦变形模量，n为沉陷指数，z为压板下陷量.月壤的kc、kφ、n取值见文献［13］.

1.2.2 月壤的剪切特性

车辆在松软地面上行驶时所能产生的最大牵引力受到土壤切向抗剪切强度的限制，因此土壤的剪切特性是影响车辆在松软地面通过性的重要因素，通常用剪应力-剪切位移曲线表示.

月壤为塑性土壤，其剪应力-剪切位移的关系可采用Janosi公式［14］进行描述:

式中:c为土壤内聚力，φ为内摩擦角，K为剪切变形模量.月壤的K值一般取为0.017 8 m，月表不同位置月壤的c和φ值差别较大，如表1所示［13］.月壤c值为0.1～2.7 kPa，典型值为0.52 kPa，φ为25°～50°，典型值为42°.

表1 月表不同位置月壤的内摩擦角和内聚力最佳估计值

2 月球车轮地相互作用力学模型

月球车驱动车轮与月壤相互作用受力分析如图1所示.z为车轮最大沉陷量;θ为轮地作用角，

图1 月球车轮地作用示意图

θ1为进入角，θ2为离去角，θm为最大应力角，θ'1为土壤变形起始角;ω为车轮转动角速度，v为车轮前进线速度.W和fDP为车体通过轮轴作用于车轮上的力，W为法向载荷，fDP为前进阻力，T为电机驱动力矩;r为车轮半径，b为车轮宽度，h为轮刺高度，R=r+h为车轮最大外圆半径.

松软月壤对车轮的作用力表现为连续的应力形式，包括正应力σ(σ1，σ2)和剪应力τ(τ1，τ2).对应力分布进行积分，可以得到公式(4)用于进行法向支持力FN、挂钩牵引力FDP和驱动阻力矩MR的计算，当车轮稳定运行时，分别与车轮负载W，电机驱动力矩T、前进阻力fDP平衡:

式中:b为车轮宽度，rs=r+λh(0≤λ≤1)，为车轮的等效剪切半径，这是一个等效的平均半径，相当于在该半径处，与车轮固结到一起的土壤和地面土壤发生相对移动.轮地作用的重要状态变量滑转率s也采用该半径定义:

结合Wong-Reece轮地作用正应力分布模型［15］和Bekker的土壤承压模型，考虑车轮的滑转沉陷，可得到式(5)～(9)用于进行正应力分布计算:

剪切应力可以用式(3)进行计算，考虑车轮的轮刺效应，土壤剪切位移计算修正公式为

上述公式中，c1和c2为最大应力角系数，c3为离去角系数，统称为轮地作用接触角系数.土壤沉陷指数n通常为一固定值，正应力σ的计算模型中，式(5)是反映车轮滑转沉陷的关键公式，用随滑转率线性变化的N代替了传统模型中的n，引入沉陷指数系数n0和n1进行N的计算［1］.式(10)则是反映车轮轮刺效应的关键，由于轮刺的作用，土壤的变形从θ'1角度开始，这对于土壤的剪切位移和应力影响都很大，半径Rj∈［r，r+h］，在较低滑转率下沉限量较小，Rj近似为R，在滑转率较大的情况下，Rj近似为r.

可以看出，轮地作用计算模型中包含了土壤的所有力学特性参数，而没有直接包含物理特性参数.其中，月壤密度ρ主要影响由于车轮沉陷而移除的土壤的重力，进而对轮地作用力产生影响，这部分相对较小，可以忽略.而月壤粒度分布、孔隙比和相对密实度对于轮地作用的进入角、离去角和最大应力角等产生影响，体现为模型中的轮地作用接触角系数，另外，对于土壤的力学特性参数也会有一定影响.因此，上述模型实际上包含了与轮地作用相关的所有月壤物理和力学特性，因此，可以通过分析模型中参数变化对于轮地作用力的影响来了解月壤特性的影响.

3 模型参数对于月球车轮地相互作用力的影响分析

采用模拟月壤，基于车轮-土壤相互作用测试平台，对宽度为165 mm，半径为157.4 mm的轮刺式车轮进行试验，试验中垂直载荷为W= 80 N，车轮速度为v=10 mm/s，滑转率设置为0～0.6，并利用等效剪切半径rs进行滑转率修正.采用压板试验和剪切试验测量模拟月壤参数，对于无法测量的参数，利用试验数据进行估计，轮地作用模型中的土壤参数值如表2～表4中的第一组数据所示.

通过准静力学分析可以得到月球车轮地相互作用过程中的垂直载荷W，因此，W通常被作为已知量;滑转率s可以作为独立变化的变量.如果土壤参数、车轮参数和垂直载荷已知，给定滑转率s，便可以求解车轮的沉陷量、驱动力矩和挂钩牵引力.因此，主要分析车轮沉陷量z，驱动阻力矩MR和挂钩牵引力FDP对于土壤参数变化的敏感度和变化趋势.敏感度的分析方法主要有解析法、数值法和两者混合的半解析法.虽然轮地作用模型为解析模型，但是模型是相互耦合的积分方程组，用解析法直接进行分析非常困难，因此主要采用数值方法，并结合理论公式进行分析.

3.1 承压特性参数的影响

令Ks=kc/b+kφ，称之为轮地作用组合沉陷模量，是车轮宽度的函数.由于kc/b≪kφ，b= 0.1 m时，月壤的kc/b部分与kφ的比值为1.5%，随着车轮宽度增加此值进一步减小.对于试验用模拟月壤和试验用车轮，kc/b与Ks的比值仅为3.8%.因此，可以忽略参数kc的影响，只分析Ks的影响，与参数kφ的影响一致.

表2为进行数值计算所采用的承压特性参数(Ks的单位为kPa/mN)以及计算出的z，FDP和MR与试验数据相比较的最大相对误差，利用最大相对误差反应轮地作用对于土壤参数变化的敏感程度，图2反映了承压特性参数对于车轮沉陷量的影响，图3是正应力和剪切应力的分布曲线.

表2 承压特性参数及模型计算最大相对误差

根据图表中的结果和轮地作用力学模型，可以得出如下结论:与沉陷量相比，承压特性参数对于挂钩牵引力和驱动阻力矩影响较小;由于车轮的沉陷量z远远小于1 m，根据指数函数的性质，正应力是关于沉陷指数系数n0和n1的减函数，而车轮的法向载荷主要由正应力的法向分量平衡，因此，n0和n1增大，固定的载荷W引起的车轮沉陷量也增加，相当于降低了土壤的承载能力;与之相反，Ks的增加会引起车轮沉陷量的减小，相当于增加了土壤承载能力;沉陷量的增大会由于对剪切位移产生影响而导致驱动阻力矩的增加，同时，土壤阻力增加，使得挂钩牵引力减小;从第1组和第8，9组的结果可以看出，Ks，n0和n13个参数并不是互相独立的，只有两个起主要作用，因此可以假设Ks为一典型值，只用n0和n1即可表征车轮和土壤作用过程中土壤的承压特性.

图2 承压特性参数对于车轮沉陷量的影响

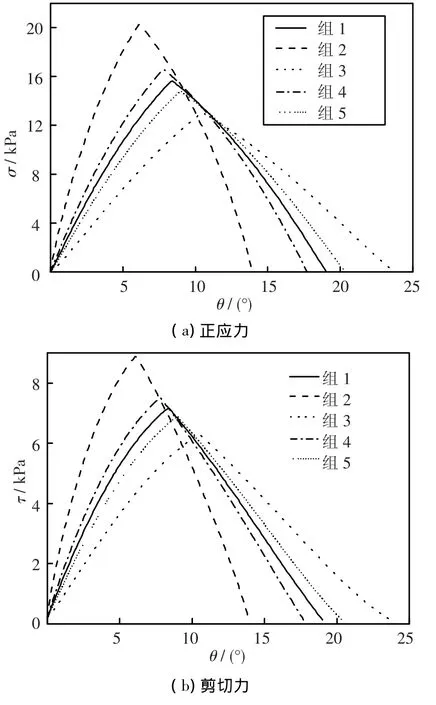
图3 承压特性参数对于应力分布的影响

3.2 剪切模型参数影响分析

表3列出了土壤的剪切特性参数的选取以及计算结果相对误差.图4为剪切特性参数对于FDP和MR的影响曲线.

表3 剪切特性参数及模型计算相对误差

图4 剪切特性参数对于FDP和MR的影响

分析表3及图4可知:剪切特性参数对于沉陷量影响很小，因而对于正应力分布的影响也不大;忽略正应力的影响，对FDP和MR的计算公式进行分析，可以看出，它们是关于c和tan φ的增函数，是关于K的减函数，图中曲线也证明了这一点;相对而言，内聚力c和内摩擦角φ对于各个滑转率下的FDP和MR都有影响，而剪切变形模量K主要决定曲线上升过程，对于较低滑转率下FDP和MR的影响比较明显;从第1组和第8组的承压特性参数可以看出，差别较大的剪切特性参数可以具有相近的集中力/力矩计算结果，说明3个参数也并非完全独立，而是有一定的相关性.

3.3 接触角系数影响分析

目前，对于月球车等星球车轮地作用接触角系数的研究相对较少，通常假定c1=0.5，c2=0，c3=0.为了了解这3个接触角系数对于轮地相互作用的影响，给定一个较大的变化范围，分析z，FDP和MR的变化情况.接触角系数及最大相对计算误差如表4所示，接触角系数对于z和FDP的影响如图5所示.

对于第5组数据，c2的设定值与估计的数据差别很大，主要是为了进行变化趋势分析，与实际情况并不相符.从其余6组数据来看，轮地作用中的力和沉陷量对于接触角系数的变化并不是特别敏感，c1，c2和c3的变化对于MR的影响几乎可以忽略，因此在研究中为了简化问题给定接触角系数的典型值是可以接受的.相对而言，这些系数对于FDP的影响最为明显.从变化趋势来讲，沉陷量固定，随着c1和c2的增大，最大应力角增加，应力值减小，产生的法向支持力减小，因而在法向载荷固定时，沉陷量是关于c1和c2的增函数，而挂钩牵引力则随着沉陷量的增加而减小;c3对于轮地作用的影响趋势可以通过理论分析得到，随着c3的增大，沉陷量增大，同时挂钩牵引力减小.

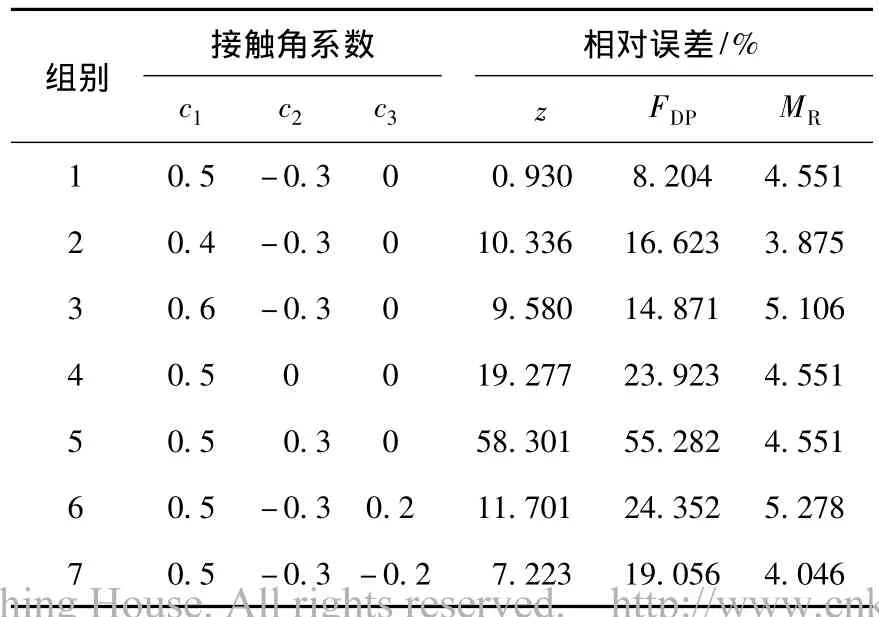
表4 接触角系数及模型计算相对误差

图5 接触角系数对z和FDP的影响

4 结论

1)土壤的承压特性主要对z产生影响，而对于FDP和MR的影响较小，n0和n1增大或者Ks的减小都会导致车轮沉陷量的增加，3个参数有一定相关性，可以指定Ks为一典型值，通过调整n0和n1的数值对车轮的沉陷量进行预测.

2)土壤的剪切特性对于z影响非常小，FDP和MR是关于c和φ的增函数，关于K的减函数，c和φ对于各滑转率下的作用力和力矩都产生影响，而剪切变形模量K主要影响较低滑转率下力和力矩的上升过程.

3)轮地作用对于接触角系数的变化并不是特别敏感，在研究中给定接触角系数的典型值是可以接受的，相对而言，这些系数对于FDP的影响最为明显.

4)从月壤参数辨识的角度而言，z与承压特性参数，MR与剪切特性参数，FDP与轮地作用接触角系数的相关度是最大的，因而可以测量z，MR和FDP，分别对相关土壤参数进行辨识和估计.

［1］丁亮，高海波，邓宗全，等.基于应力分布的月球车轮地相互作用地面力学模型［J］.机械工程学报，2009，45(7):49-55.

［2］NAKASHIMA H，FUJII H，OIDA A，et al.Parametric analysis of lugged wheel performance for a lunar microrover by means of DEM［J］.Journal of Terramechanics，2007(44):153-162.

［3］BAUER R，LEUNG W，BARFOOT T.Experimental and simulation results of wheel-soil interaction for planetary rovers［C］//Proceedings of the IEEE/RSJ Int Conf on Intelligent Robots and Systems.Piscataway:IEEE Robotics and Society，2005:586-591.

［4］LIU Jicheng，GAO Haibo，DENG Zongquan.Effect of straight grousers parameters on motion performance of small rigid wheel on loose sand［J］.Information Technology Journal，2008，7(8):1125-1132.

［5］LIU Jicheng，GAO Haibo，DENG Zongquan，et al. Effect of slip on tractive performance of small rigid wheel on loose sand［J］.Springer Intelligent Robotics and Applications of Lecture Notes in Computer Science，2008，5314(1):1109-1116.

［6］DING Liang，GAO Haibo，DENG Zongquan，et al. Wheel slip-sinkage and its prediction model of lunar rover［J］.Journal of Central South University of Technology，2010，17(1):129-135.

［7］YOSHIDA K，ISHIGAMI G.Steering characteristics of a rigid wheel for exploration on loose soil［C］//Proc of the 2004 IEEE Int Conf on Intelligent Robots and Systems.Piscataway:IEEE Robotics and Society，2004: 3995-4000.

［8］叶培建，肖福根.月球探测工程中的月球环境问题.航天器环境工程，2006，23(1):1-11.

［9］CARRIER W D，OLHOEFT G R，MENDELL W.Physical properties of the lunar surface［M］.Lunar Source book. New York:Cambridge University Press，1991:475-594.

［10］郑永春，欧阳自远，王世杰，等.月壤的物理和机械性质［J］.矿物岩石，2004，24(4):14-19.

［11］庄继德.计算汽车地面力学［M］.北京:机械工业出版社，2002.

［12］BEKKER M G.Introduction to terrain-vehicle［M］.［S.l.］:The University of Michigan Press，1969.

［13］APOSTOLOPOULOS D S.Analytical configuration of wheeled robotics locomotion［R］.Pittsburgh:The Robotics Institute of Carnegie Mellon University Technical Report，2001:CMU-RI-TR-01-08.

［14］JANOSI Z，HANAMOTO B.Analytical determination of drawbar pull as a function of slip for tracked vehicle in deformable soils［C］//Proc 1st International Conference of ISTVS.Torino:International Society for Terrain-Vehicle Systems，1961:707-726.

［15］WONG J Y，REECE A R.Prediction of rigid wheel performance based on analysis of soil-wheel stresses，part I: performance of driven rigid wheels［J］.Journal of Terramechanics，1967，4(1):81-98.