运输服务业中基于期权的存量控制方法研究
2010-03-12杨清清陈浩凯
杨清清,陈浩凯
(1.国防科学技术大学 信息系统与管理学院,湖南 长沙 410073; 2.长沙理工大学 期刊中心,湖南 长沙 410076)
运输服务业包括航空客运、航空货运、铁路运输、公路、水路运输等,主要通过在有限的销售时间内销售有限的存量来获取收益,到一个时间点,其未被售出的产品或服务的价值将变得很低甚至骤降为零,如,在航班起飞后航班上没有售出的座位(或机票)价值就变成零了,这样的产品通常称之为易逝品。收益管理是对易逝品进行管理、实现其收益最大化的有效方法。存量控制和超订是收益管理的核心内容,存量控制是指通过对运输存量向不同顾客群体出售的数量加以控制的过程,达到企业收益最大化目的。超订是指企业售出或预定的产品数量超出其实际拥有的存量数量,比如机票一类的运输服务产品,购买时间和消费时间是相分离的,已经购买或预定了机票的顾客很有可能因为种种原因退订或无法登机,造成航班座位的虚耗,给航空公司造成收益损失。但超订可能出现的风险就是超售,如果出现的顾客数超出额定存量数,企业须对不能提供服务的顾客给与补偿。
传统的收益管理理论只研究单纯的存量控制问题,即指在存量控制问题的研究中不考虑超订或顾客选择行为,并且价格是外部变量,也不考虑企业之间的竞争,通过使存量边际收益最大化的方法,来达到收益最大。也有学者对运输服务业中单纯的存量控制问题进行研究,其中还有人讨论了存在群订时的存量控制问题。[1-10]
本文考虑研究存量控制和超订的联合决策问题,提出把期权方法应用到运输服务业的订购过程中,期权给予合同的持有者在一定的时间,以确定的价格,从对手那里买进或卖出某种资产的权力。在这一订购过程中应用两种类型的期权:第一种提供给顾客附带买入期权的产品(顾客是该买入期权合同的空头),并且在期权合约中被告知“这种附带买入期权的产品价格比较低,但是在订购过程的后续阶段可能会被召回,并给与一定的补偿费。”运输服务企业(买入期权合同的多头、持有者)享有在规定期限内买入该运输产品的权利,企业可以通过附带买入期权把最低价位的产品存量售出,以便随时召回;那么在需求高的情况下,可更好的针对时间不敏感的顾客群提供服务,在需求低的情况下,也可以吸引原本不选择该交通方式的顾客。同时也可降低因超售引起的潜在损失,还可以有效减少不可控因素(如天气、需求、能源价格等因素)的负面作用。第二种是运输服务企业向其代理机构出售一部分附带卖出期权的产品。如果企业(卖出期权的多头、持有者,其有权在将来某一确定的时间以某一确定的价格出售)向执行卖出期权,那么代理结构(卖出期权的空头)就必须购入企业多余的存量。在期权合约中,执行价和到期日都明确给出。假定两种情况都是在订购过程的第一个时间段购买,在最后一个时间段执行,如果需求比期望值要高,企业将执行买入期权,反之,则执行卖出期权。
一、基于期权的存量控制模型建立
(一)模型描述
假设销售方在有限的时间内销售c个运输服务产品(例如座位、舱位等),在销售期结束后剩余产品的价值为零。假设订购过程由离散的时间段组成,从订购过程的开始时间段1到销售期结束的最后时间段t,分为j(j=1,2,…,t)个时间段。运输服务产品可分为i(i=1,2,…,n)个等级,假设每个等级的产品数量相等,每个等级产品的存量水平为c′(c′=c/n),价格为fi,假定价格数量是有限的,且f1 出售的买入卖出期权的数量在产品订购过程的第一阶段,由期望需求、存量水平和允许卖出的期权数量的最大值来确定。即: (1) (2) 执行的买入卖出期权的数量在最后一个阶段决定,即: (3) (4) 授权水平计算如下: (5) 式中:aij为第j阶段时,对第i登机产品的授权水平;r为预期顾客未出现(登机、乘车等)的概率;式中其他符号含义同上。 订购水平由授权水平决定,如下列公式(6)所示: (6) 式中:bij为第j阶段时,对第i等级产品的授权水平;dij为第j阶段时,对第i等级产品的需求水平;式中其他符号含义同上。 被拒绝服务的数量ndb可以用公式(7)计算: (7) 式中ndb为被拒绝服务的数量;r′为顾客未出现(登机、乘车等)的概率的实际值;式中其他符号含义同上。 由此可得,收益R为: (8) 式中:Pp为卖出期权的期权价格;Pc为买入期权的期权价格;πp为卖出期权的执行价格,与最低产品价格f1相等;πc为买入期权的执行价格;cdb为拒绝提供服务的平均成本; 收益可以由公式(8)计算,收益为卖出产品所获得的总价格,减去执行买入期权的成本、拒绝服务的赔偿成本和买入卖出期权的期权价格。 运输服务企业在有限的时间内销售100个产品,销售实践分为5个时间段,即t=5,产品等级数n=4,则c′=25。期望需求E(dij)与实际需求dij均服从泊松分布,参数为λ=7。1、2、3、4等级产品的价格(元)分别为2000,23000,2500,3000。其他参数如下:r=0.2,r′=0;pc=pp=100;cdb=1000;πp=πc=2700。 计算步骤及结果如下: 首先,期望需求E(dij)与实际需求dij用同样的方法,应用matlab产生随即数,相应与5个时间段、4种产品等级产生5行4列的随机数,第i行j列的数字表示在第i个时间段对第j等级产品的期望需求。 由公式(1-1)和公式(2)有: (np,1,np,2,np,3,np,4)=(0,0,2,0),(nc,1,nc,2,nc,3,nc,4)=(2,12,0,13)。 已知(np,1,np,2,np,3,np,4),且E(dij)矩阵已由随机数产生,又已知r=0.2,由公式(5)授权水平的前4个时间段即可确定。 dij矩阵已通过matlab随机产生,由公式(1-6)可确定订票水平的前4个时间段的数值。 又因为已知ndb=4,由公式(8)可得R=240300。 本文研究存量控制和超订的联合决策问题,并将期权的思想引入其中,在运输服务产品的订购过程中应用两种类型的期权:顾客购买产品的同时购买一个买入期权;或是运输服务企业向其代理机构出售一部分附带卖出期权的产品。通过确定两种期权的出售数量、执行数量及订购量,进行存量控制。 通过出售附带买入期权的产品,运输服务企业可以避免因超售而出现的拒绝服务的赔偿成本以及一些会造成未来经济损失的无形成本。每当需求比期望值高时,可以运用买入期权带来的灵活性,把产品卖给支付意愿高的顾客。同样,当需求比期望值低时,企业可以利用卖出期权以确定的价格(一般来说,比现价低)把产品卖给代理,以避免空座的情况发生。所以,潜在的损失仅限于支付的期权费。这种灵活性,不但减少了超售赔偿成本、忠诚度成本,降低了空座率,并且提高了当需求足够多时服务支付意愿高的顾客的可能性,从而较大程度地提高了运输服务企业的总收益。但这种方法并没有解决以什么执行价格出售多少买入卖出期权的问题。可能会出现如下情况,如运输服务企业持有过多的卖出期权,而支付意愿高的顾客的需求量比预期高得多,那么既使企业支付了卖出期权的费用,也不愿意执行卖出期权。买入期权也有类似的问题。这是进一步研究的重点。 [参考文献] [1]Littlewood K. Forecasting and Control of Passenger Bookings [J]. 12thAGIFORS Symposium Proceeding, Nathanya, Israel, 1972, 12: 95-117. [2]Belobaba P P. Air Travel Demand and Airline Seat Inventory Management [D]. Ph.D. thesis, Flight Transportation Laboratory, Massachusetts Institute of Technology, Cambridge, MA, 1987. [3]Belobaba P P. Application of a Probabilistic Decision Model to Airline Sear Inventory Control [J]. Operations Research, 1989, 37(2): 183-197. [4]Kleywegt A J,Papastavrou J D.The Dynamic and Stochastic Knapsack Problem[J].Operations Research,1998,46:17-35. [5]Brumelle S L, McGill J I. Airline Seat Allocation with Multiple Nested Fare Classes [J]. Operations Research, 1993, 41: 127-137. [6]Robinson L W. Optimal and Approximate Control Policies for Airline Booking with Sequential Non-monotonic Fare Classes [J]. Operations Research, 1995, 43: 252-263. [7]Lee T C, Hersh M. A Model for Dynamic Airline Seat Inventory Control with Multiple Seat Bookings [J]. Transportation Science, 1993, 27:252-265. [8]Lautenbacher C J, Stidham S J. The Underlying Markov Decision Process in the Single-Leg Airline Yield Management Problem [J]. Transportation Science, 1999, 33:136-146. [9]Brumelle S, Walczak D. Dynamic Airline Revenue Management with Multiple Semi-Markov Demand [J]. Operations Research, 2003, 51(1): 137-148. [10]Van Slyke R, Young Y. Finite Horizon Stochastic Knapsacks with Applications to Yield Management [J]. Operations Research, 2000, 48: 155-172.(二)模型构建


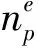
二、数值例子
三、结论
