基于自干涉驱动技术的超声波飞行时间测量系统优化设计

王雪峰，唐祯安

(大连理工大学电子科学与技术学院，辽宁大连116023)

作为超声波测距、超声波流量计量中的关键技术，超声波飞行时间测量技术越来越受到人们的重视［1－2］。为提高检测精度，包括阈值检测在内的很多方法已成功应用到工业测量的各个领域［3－6］。然而，随着检测精度要求的逐步提高，超声波换能器与流场之间的阻抗不匹配、测量环境复杂多变、换能器激发迟滞等问题，严重地阻碍了传统测量方法的继续推广与应用［7－8］。

图1所示为超声波换能器接收信号压电转换迟滞现象示意图。脉冲信号经流场由发射换能器向接收换能器传播。超声波信号到达接收端，接收换能器经压电转换将传播信号转化为电压信号。当接收信号电压幅值超过预先设定的电压阈值时，通过计算信号到达时间与发射脉冲的时间间隔即可得到超声波飞行时间。实际测量中，压电换能器、工况条件及换能器间的相对距离都会改变接收信号迟滞时间，影响超声波飞行时间的检测精度［9］。

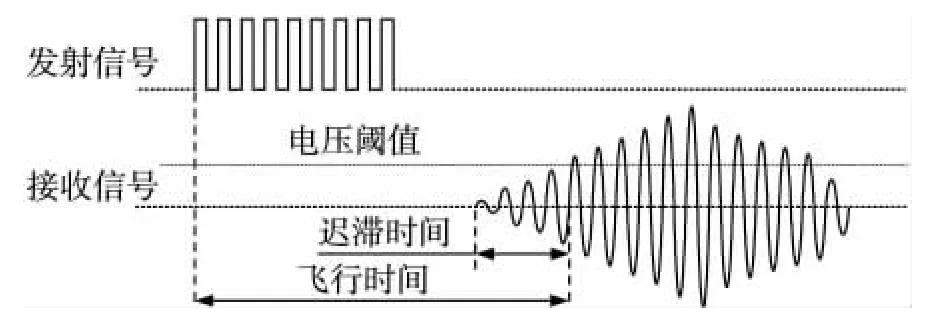
图1 超声波换能器接收信号压电转换迟滞示意图

此外，在实际测量中受环境噪音的干扰，超声波接收信号会发生变形，产生阈值检测偏差［10］。情况严重时，初始到达低幅值超声波信号会完全淹没在噪音中。此种条件下，接收波形经阈值检测后会出现错波或漏波，极大的影响了结果的准确性［11］。为解决上述问题，本文结合自干涉驱动技术与双阈值拟合算法，提出了一种测量超声波飞行时间的新方法。

1 自干涉驱动技术

方波脉冲信号经超声波换能器转换后形成衰减的正弦波［12］:

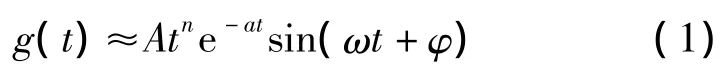
其中，n，a，ω，φ为换能器特性参数，A为脉冲波幅值，ω是换能器谐振角频率，t代表超声波传播时间。假设由同一发射换能器产生两列连续的脉冲波:

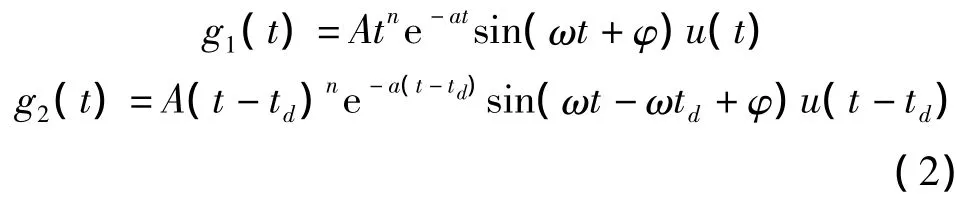
td为脉冲波的时间间隔，u(t)代表单位阶跃函数。叠加两列脉冲波形成组合脉冲序列:

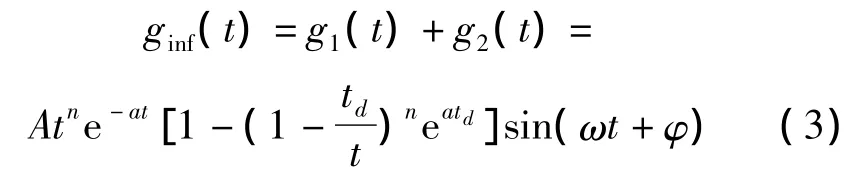
当时间间隔td=(2k+1)π/ω小于等效信号波长，由式(2)可知，前后发射脉冲波形经超声波换能器转换后存在干涉现象，波形相位翻转180度。此外，当传播时间满足式(4)的条件时，发射信号波形产生包络线过零点。

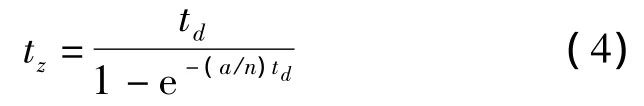
根据上述公式推导，通过计算发射、接收信号的包络线过零点时间间隔可以直接得到超声波信号在换能器间的传播时间。然而实际测量中，由于噪声干扰经常淹没包络线过零点，常规的过零点检测方法容易产生测量误差。为克服这一问题，本文通过调节发射脉冲波的时间间隔产生自干涉驱动波形，利用接收信号包络线过零点前后相位翻转现象，通过CPLD相位检测技术测量相位翻转时间从而确认接收信号到达时间。

图2所示为自干涉驱动波示意图。自干涉驱动信号由三部分组成:①发射换能器输出一列6个低幅值驱动脉冲(脉冲#1);②当第一列脉冲输出后，2个高幅值脉冲按相反相位激发换能器(调节脉冲);③相位、幅值调节后，保持相位、幅值输出第二列6个脉冲(脉冲#2)。通过调节脉冲的相位、幅值使顺序发射两列脉冲波自干涉出现包络线过零点。经实际检测校准，将调节脉冲第二个脉冲波的上升沿作为发射脉冲相位检测触发信号。

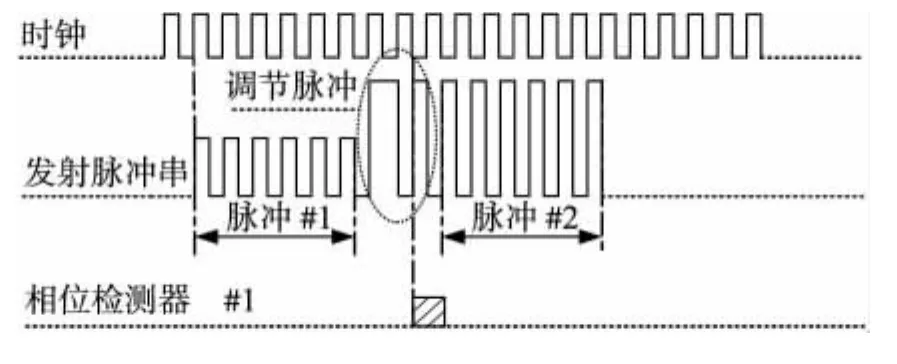
图2 自干涉驱动波示意图

图3为接收信号相位检测飞行时间示意图。自干涉驱动波经流场由发射换能器向接收换能器传播。超声波信号到达接收端，经放大、滤波电路调理后与比较器预先设定的电压阈值进行比较。当接收信号超过电压阈值时，比较器输出翻转，触发信号同步锁存进CPLD供相位检测模块调用。系统中CPLD通过设定计数器实现两项功能:①超声波发射信号及比较器触发信号时间间隔计数;②接收信号脉宽检测。实际测量中，当比较器触发信号产生脉宽异常时，系统利用CPLD计数功能对接收脉宽进行校准。若满足预先设定检测要求，初始相位翻转时间即为接收信号到达时间。最后，CPLD计数器计算发射脉冲及接收信号相位翻转时间差得到超声波飞行时间。

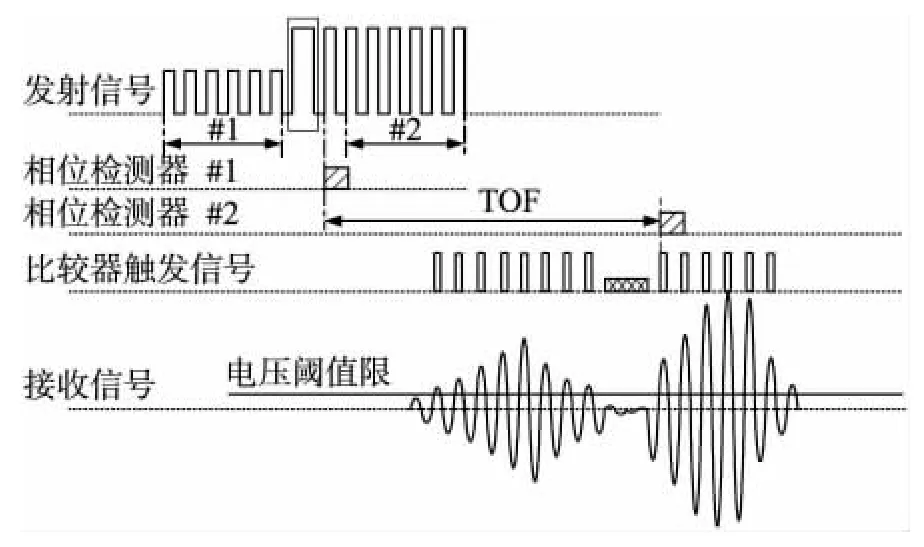
图3 超声波飞行时间相位检测原理图

2 双阈值拟合算法

本文设计的超声波飞行时间测量系统通过检测比较器触发信号完成接收波形相位检测。考虑到触发信号与CPLD计数脉冲存在同步偏差，检测精度受比较器阈值限制，该方法很难准确定位相位翻转初始时间即接收信号包络线过零点。为克服上述问题，本文结合数值拟合方法，对包络线过零点通过数值计算精确定位。图4所示为包络线过零点双阈值拟合算法示意图。V1，V2为比较器设定检测阈值，t1，t2表示比较器翻转时间，t0表示接收信号自干涉波形过零点。该方法利用两点接收信号检测数据，将超声波信号上升沿近似拟合为指数函数形式，形如:A=a(t－t0)n。其中，A为接收信号拟合计算电压值，a为接收波形幅值参数，t0为接收脉冲到达时间，t为脉冲传播时间，n为曲线拟合参数。为确定该函数最合理的幂指数数值，我们将拟合函数与实际接收波形进行比较。通过对比，接收信号上升沿与n=2时的拟合函数吻合程度最高，因此抛物线函数被选定为包络线过零点计算的拟合函数。

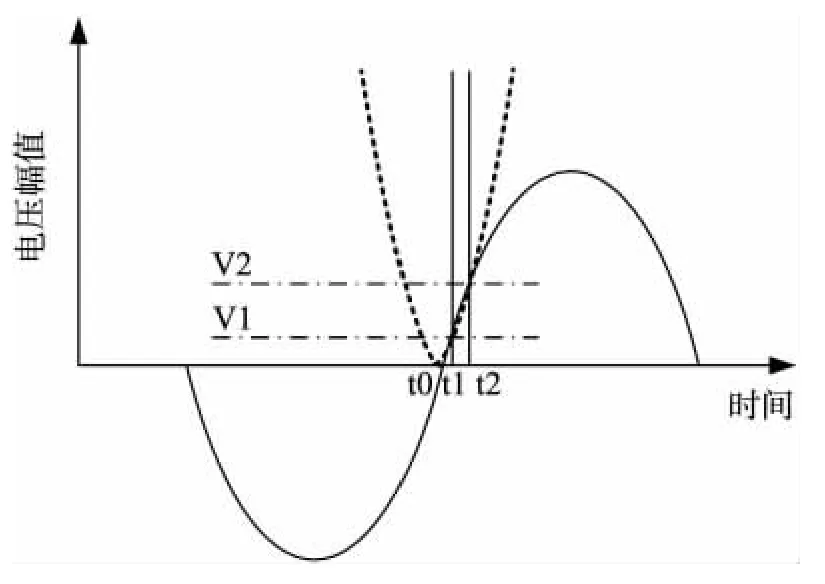
图4 双阈值拟合算法原理图

为简化系统设计，本文利用双比较器实现相位侦测及接收信号阈值测量，结果如式(5)、式(6)所示。当比较器1监测数据显示接收波形出现相位翻转，比较器2打开并按预先设定阈值对接收信号进行检测。通过对双比较器检测数值推导计算，实现接收信号包络线过零点求解，结果如式(7)所示:

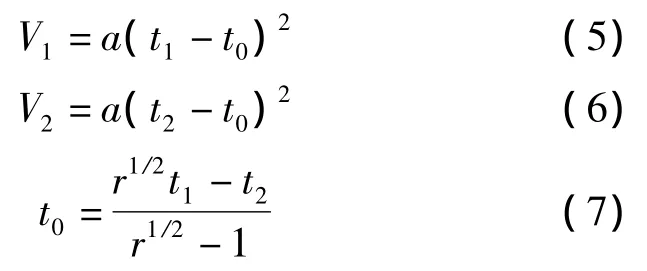
其中，r=V2/V1为接收波形上下限阈值电压之比。经实验验证，采用比较器阈值检测技术进行过零点测量，不需要非线性迭代计算推导拟合参量，能够极大的降低计算成本，简化计算步骤。

为衡量算法的稳定性及测量误差容限，本文利用式(5)、式(6)的推导公式(t2－t1)2=(V1/a)·(r1/2－1)2，对式(7)进行微分计算，结果如式(8)所示:

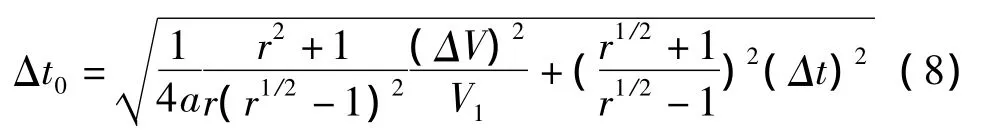
式(8)结果表明，调节比较器设定的阈值可以改变系统测量精度。当比较器1阈值范围设置过低，阈值检测容易受到环境噪声干扰，系统检测稳定性将变差。此外，两个阈值比较器设定数值之比增加也会造成系统检测不稳定。对比实验结果，当r的取值范围控制在1.5－2.5之间，系统稳定性最高且过零点测量结果最准确。

3 硬件设计

系统硬件由模拟电路和数字电路两部分组成如图(5)所示。核心器件为TI公司的数字信号处理器DSP TMS320F2812及Xilinx公司的复杂可编程逻辑器件CPLD XC2C128。其中，DSP负责时间调控、拟合算法处理、飞行时间综合计算及外围模块管理。CPLD负责驱动波形激励、接收波形脉宽校准以及飞行时间整周期计数。系统启动后，由CPLD、电压控制模块生成40 kHz自干涉驱动波激励超声波换能器。图6所示为CPLD趋动波形时序仿真及幅值电压控制模块硬件原理图。由图可见，自干涉驱动波由40 kHz时钟经相位、幅值调节后生成。CPLD利用分频器对40 MHz晶振分频产生两组相位相反的40 kHz辅助时钟，并根据驱动波自干涉条件设定相位、幅值控制信号。在相位控制信号的上升沿、下降沿，系统触发不同的辅助时钟，完成驱动波形的相位调节。幅值调节电路由电容、稳压器(7 805)、三极管(2SC1815)及分压电阻构成。当CPLD输出3.3 V幅值控制信号，三极管工作在饱和区，稳压器输出端旁路电阻R3直接与地连接，输出电压为5 V。当CPLD输出0 V幅值控制信号，三极管工作在截止区，调整R2、R3电阻值，输出端电压将达到12 V。因此，通过调控CPLD的幅值控制信号可以产生5 V、12 V变化的驱动电压。最后，经CPLD相位调节后的驱动信号输入到开关场效应管栅极，输出端将产生幅值变化的自干涉驱动波。

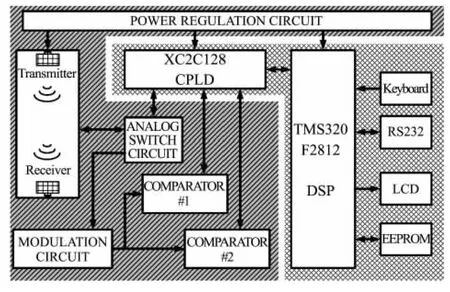
图5 系统硬件结构图

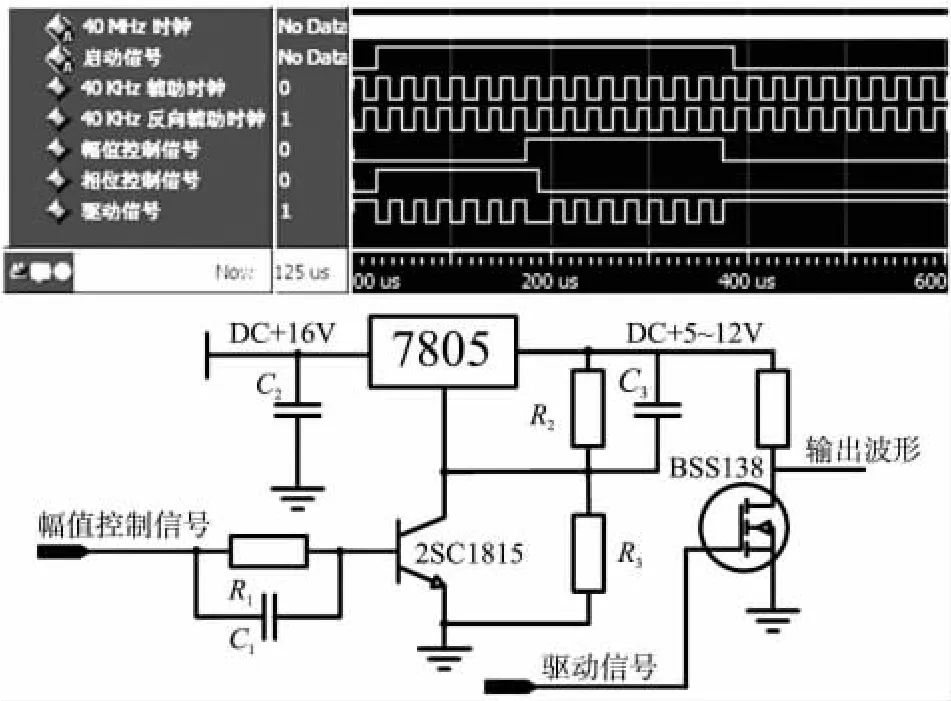
图6 自干涉驱动波时序仿真及硬件原理图

自干涉驱动波经发射换能器激励后向接收换能器传送。超声波信号抵达接收端，经放大、滤波调理电路处理后输入到阈值比较器1。当输入结果超过比较器预先设定的触发值时，比较器翻转并锁存触发时间进CPLD。CPLD脉宽检测模块通过对比较器1触发生成的脉冲进行脉宽检测判断接收信号相位是否出现翻转。如果脉宽检测发生变化即认为接收信号出现相位翻转，比较器2启动并按预先设定值对接收波形二次比较及同步锁存触发时间。最后，CPLD检波单元对比较器1、2采集到的脉宽信号综合校验。当检测结果满足脉宽设计要求，比较器触发时间将传送至DSP利用拟合算法计算超声波飞行时间。

4 测试及结果

为验证系统的有效性，将超声波飞行时间检测结果输入如图7所示的超声波测距实验平台。

图7 超声波测距系统实验平台

检测平台经光学系统校准后检测范围为20 mm～200 mm，两个超声波换能器面对面安装在检测平台两侧。自干涉驱动波由发射换能器经空气向接收换能器传播。信号到达接收端后，系统对比较器触发信号进行处理，得到超声波飞行时间。通过式(9)计算探头间距。

其中，STOF为超声波传输距离，C为超声波在空气中传播速度，TTOF为系统检测得到超声波飞行时间。在实验室环境下，为规避无关因素干扰，有效提高检测精度，系统以20 mm作为步长单位在40 mm至180 mm间改变检测距离。相对误差计算公式如式(10)所示。其中，Sstandard为光学校准的标准检测距离，Erelative表示测量结果与标准值之间的相对误差。结果如图8所示:

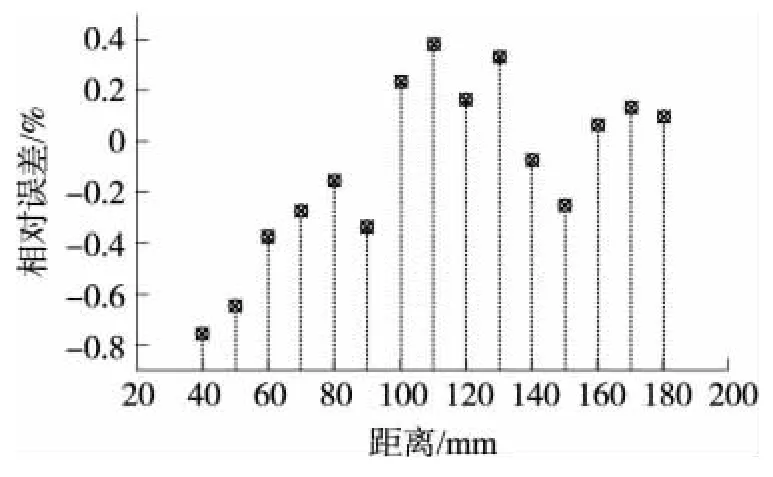
图8 不同间距条件下超声波测距检测相对误差

5 结论

本文结合双阈值拟合算法，将自干涉驱动波技术应用于超声波飞行时间测量，克服了以往阈值检测中压电换能器迟滞时间不确定、信号到达触发时间不同步等问题，增强了系统抗干扰能力并有效地提高了系统稳定性。同时，系统凭借DSP高速信号处理器的数据处理能力、CPLD复杂可编程逻辑器件的高效相位检测功能，结合双阈值拟合算法，保证了系统检测的实时性，提高了测量分辨率。为验证系统性能，本文将超声波飞行时间计算结果带入超声波测距实验平台。实验结果表明在40 mm到180 mm测量范围内，相对误差绝对值小于0.8%，平均误差小于0.4%。对比飞行时间普通阈值检测技术，本系统提出的检测方法有效地提升了检测精度。通过重复性实验，系统稳定性及重复性相比常规方法也有大幅度提升。

［1］Lynnworth L C.Ultrasonic flowmeters［J］.IEEE Transactions on Instrumentation and Measurement，1981，3:217－223.

［2］Daniele Marioli，Claudio Narduzzi，Carlo Offelli，et al.Digital Time-of-Flight Measurement for Ultrasonic Sensors［J］.IEEE Transactions on Instrumentation and Measurement，1992，41(1):93－97.

［3］Lynnworth L C，Liu Y.Ultrasonic flowmeters:Half-Century Pro-gress Report，1955－2005［J］.Ultrasonics，2006，44(1):1371－1378.

［4］Barshan B.Fast Processing Techniques for Accurate Ultrasonic Range Measurements［J］.Measurement Science and Technology，2000，11:45－50.

［5］刘晓宇，杨江.时间比例放大技术在超声波流量计中的应用［J］.传感技术学报，2007，20(2):454－457.

［6］Huang Y S，Huang Y P.An Accurate Temperature Measurement System Based on an Envelope Pulsed Ultrasonic Time-of-Flight technique［J］.Review of Scientific Instruments，2007，78:102－112.

［7］王铭学，王文海，田文军，等.数字式超声波气体流量计的信号处理及改进［J］.传感技术学报，2008，21(6):1010－1014.

［8］Raya Y，Frizera A，Ceres R，et al.Design and Evaluation of a Fast Model-Based Algorithm for Ultrasonic Range Measurements［J］.Sensors and Actuators A:Physical，2008，148:335－341.

［9］Huang K N，Huang C F，Li Y C，et al.High Precision，Fast Ultrasonic Thermometer Based on Measurement of the Speed of Sound in Air［J］.Review of Scientific Instruments，2002，73(11):4022－4027.

［10］Sasaki K，Tsuritani H，Tsukarnoto Y，et al.Air-Coupled Ultrasonic Time-of-Flight Measurement System Using Amplitude-Modulated and Phase Inverted Driving Signal for Accurate Distance Measurements［J］.IEICE Electronics Express，2009，6:1516－1521.

［11］周艳，王润田，梁鸿翔.声时测量精度的主要影响因素分析［J］.声学技术，2008，27(2):210－213.

［12］Cai CH，Regtien PPL.Accurate Digital Time-of-Flight Measurement Using Self-Interference［J］.IEEE Transactions on Instrumentation and Measurement，1993，42:990－994.