Simple Chemical Model for Facilitated Transport with an Application to Wyman-Murray Facilitated Diffusion
2010-03-06COLEChristineLindQIANHong
COLE Christine Lind QIAN Hong
(Department of Applied Mathematics,University of Washington,Seattle,WA 98195,USA)
Wyman-Murray facilitated diffusion of oxygen by hemoglobin (Hb)or myoglobin(Mb)has long been considered a counterintuitive phenomenon in biophysical chemistry[1].To further our understanding of the physico-chemical nature of this interesting and important problem,we study the related problem in a chemical kinetic setting.Although the specific examples that we use to demonstrate our model are oxygen and carbon monoxide transport being facilitated by hemoglobin and myoglobin,the chemical kinetic theory can be applied to a much broader set of scenarios with facilitated chemical and biochemical transitions. This mechanism complements the enzyme catalysis mechanism which assumes that the chemical transition is faster when a substrateisboundtotheenzyme[2].Insection1wedescribethesimple model.Section 2 presents a comparison between our model and Wittenberg′s experimental results.In section 2.4,a potentially novel relation required to sustain the facilitation effect is established between the association-dissociation rates and the downstream ligand concentration(i.e.,back pressure).
We begin with a brief description of our motivating example.
The role of hemoglobin in enhancing oxygen transport was postulated as early as 1932 by Roughton[3].Experiments were designed and executed to measure the facilitation of oxygen transport through cells due to the presence of hemoglobin and myoglobin during the 1960′s and early 1970′s by Wittenberg,Hemmingsen,and Scholander,to name a few[4-7].Mathematical models based on reaction-diffusion equations were proposed,and approximate solutions were studied analytically by Murray, Wyman,Rubinow&Dembo,and numerically by Kreuzer& Hoofd[8-11].The theory behind this type of facilitated diffusion suggests that under certain conditions the flux of a small ligand, such as oxygen,diffusing in an aqueous solution can be enhanced by the presence of a large protein,such as hemoglobin, to which the ligand binds reversibly and rapidly.However,since the diffusion coefficient of the protein-ligand complex is orders of magnitude smaller than that of the free ligand,the phenomenon described above seems counterintuitive.To illustrate the counterintuitive nature of the problem,Wyman[9]asked“How could a fly hope to increase his rate of progress by alighting on the back of a tortoise?”It turns out,conceptually,that if a large gradient in the free ligand concentration is maintained,then the resulting phenomenological Fick′s flux of the total ligand is significantly greater when the carrier molecule is present in the system,even when the carrier molecule moves very slowly.This theory is now one of the established mechanisms by which oxygen and carbon monoxide are transported in muscle respiration, with the role of the facilitating carrier protein being played by hemoglobin and/ormyoglobin[12-14],and has also inspired the model for the phosphocreatine shuttle[15].While the reaction-diffusion mathematical models have explained the phenomenon,the focus of the present work is to describe its physico-chemical nature.
Solutions to the reaction-diffusion models provide a good match with the experimental results,but previous mathematical models were missing a simple but profound insight into the mechanism of the facilitation.We propose a simple chemical kinetic model for the facilitated transport of a ligand by a carrier molecule to which the ligand binds reversibly.The simple kinetic model provides all of the key results for Wyman-Murray facilitated diffusion.Our model shows that the facilitation by the carrier molecule is guaranteed,as long as a free ligand gradient is kept constant,due to the cell being an open chemical system[16]with respect to the ligand.
The key physico-chemical notion in this facilitated transport is that free ligand concentrations,at both the up-stream and down-stream ends of the system,are kept constant.Thus the transport is driven by a fixed chemical potential.Because of this,the presence of the carrier molecules,even though their transport rate is slow,creates additional,“parallel pathways”for transport.In the language of electrical circuitry:adding an resistor in parallel,even a very large one,always increases the overall conductance.
1 A simple chemical kinetic model revealing all complexities
The simple chemical kinetic model describes a one dimensional system in which both ligand and carrier molecules are present in solution.A schematic diagram of the system being modeled can be seen in Fig.1.The positive direction of transport is from left to right,meaning that the concentration of the ligand at the left-hand“up-stream”end of the system is larger than that at the right-hand“down-stream”end.The ligands are free to pass through the barriers at either end of the system,but the carrier molecules are not.Ligand molecules,carrier molecules, and ligand-carrier complexes move through the solution by simple gradient driven diffusion.Furthermore,the ligands bind reversibly with the carrier molecules.It will be shown that the presence of the carrier molecules will enhance the total ligand transport.

Fig.1 Model diagramSchematic diagram for the one dimensional facilitated transition system.S and P represent the free ligand at the left-hand“up-stream”end of the system and the right-hand“down-stream”end of the system,respectively.Similarly,E and represent the carrier molecules while ES and represent the ligand-carrier complexes.l denotes the distance between the two ends of the system.
The ligand-macromolecule system is a natural setting for modeling facilitated transitions.We will now use the compartmental representation for the transport and identify the ligand at the up-stream end of the system and down-stream end of the system as S and P,respectively,as in the enzymatic reaction terminology.The transport reactions are assumed to be first-order, parallel to Fick′s law for diffusion.Thus,we are effectively considering a simple biochemical kinetic model based on standard reversible Michaelis-Menten enzyme kinetics[2].Our model describes a system in which there are two conformational states of the enzyme,E andrepresenting the carrier molecule before and after a“conformational change.”The enzyme-substrate complex,ES,and enzyme-product complex,E~P,represent the ligand bound to the carrier molecule before and after the conformational change.The conformational change represents the compartmentalized transport from the up-stream end to the down-stream end of the system.The substrate can also convert to the product directly without the enzyme,corresponding to the ligand moving from one end of the system to the other in the diffusion formalism.
The chemical kinetic model can be summarized by the following set of reversible reactions:
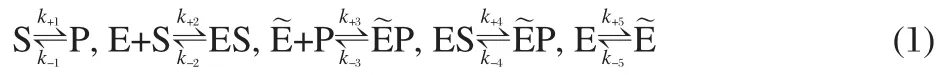
The equilibrium energy balance loop law,or detailed balance, also requires that

Let cS,cP,cE~,cE,cES,and cE~Pdenote the concentrations of the reactants.Then by the law of mass action,the concentrations of the reactants are governed by the set of six ordinary differential equations with initial conditions shown in Eq.(3):

Note that this set of initial conditions assumes that the system is initially composed of only free substrates,enzymes,and products.The initial conditions are not essential to our analysis since we are mainly concerned with the unique steady state of the system,but they are used for numerical computations.The sum of Eqs.(3c)through(3f)is zero,so the total amount of enzyme in the system is conserved,

as we expect because the enzymes(i.e.,carrier molecules)can not leave the biophysical system.
The equations as shown in Eq.(3)also have a conservation for the total ligand concentration:the sum of Eqs.(3a)through(3d) is also zero.This is the standard set-up for reactions in a closed chemical system.We discover that the kinetics of the system can be significantly different depending on whether the system is closed with respect to S and P,meaning that the total ligand concentrations in each compartment are held constant,or open, meaning that the free ligand concentrations in each compartment are held constant.In Gibbs′statistical mechanics,these are known as canonical and grand canonical ensembles,respectively[17].
Our goal is to study facilitated transport,so we will be interested in the rate enhancement of the conversion of the substrate to the product due to the presence of the carrier molecule in the steady state.We use the King-Altman-Hill method[18-19]to solve for the steady-state concentrations of the different forms of the enzyme:
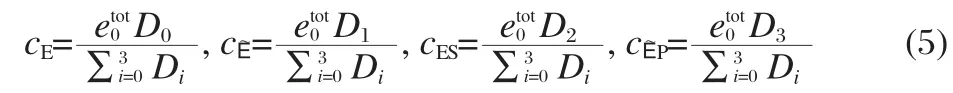
where the expressions for the Dican be found in Eq.(26)in the Supporting Information.Note that the steady-state enzyme concentrations are functions of the free ligand concentrations,cS,cP, which are assumed to be constant in the grand canonical setting, as well as in the King-Altman-Hill method[20].
1.1 Canonical scenario:constant total ligand concentrations
In the canonical scenario,the total ligand concentration in each compartment is held constant so that

Then we can use the results given above by noting that,in the steady state,the concentrations of the free ligands,cSand cP,can be calculated using Eq.(5)along with Eqs.(3a)and(3b).For the rest of this section,we will assume that k±2,k±3≫k±4,k±5,which is appropriate for studying facilitated transport since the association-dissociation reaction rates should be fast compared to the transport reaction rates.
From Eq.(5)we know that the steady-state concentrations of the free enzymes,cEand cE~,satisfy


Eqs.(4),(6),(7),and(8)give a system of six simultaneous algebraic equations,with six unknowns,cS,cP,cES,cE~P,cE,cE~,representing the steady-state concentrations of the reactants.The six simultaneous equations can be combined to yield two implicit equations containing only the free enzyme steady-state concentrations,cE,cE~,the total concentrations of the enzyme,substrate, and product,etot00,s0,p0,and the reaction rate constants:
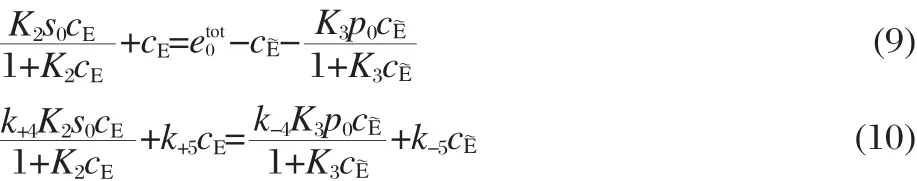
The curves described by Eqs.(9)and(10)have exactly one intersection in the cE/cE~plane corresponding to a unique steady state. In this type of Michaelis-Menten kinetics,the unique steady state is globally attractive and asymptotically stable[21].
Recall that since we are interested in the enhancement of the reaction rate for creating the product,we will examine the steady-state net reaction velocity,

where K+and K-are the apparent forward and backward rates ofThe apparent rates are given by
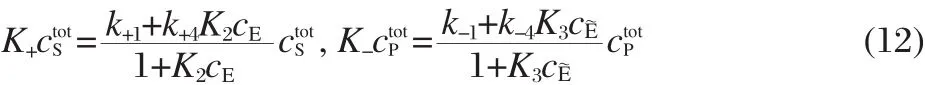
Note that

so if k+4<k+1,then the apparent forward rate has to be less than k+1. Similarly,if k-4<k-1,then the apparent backward rate is less than k-1.Therefore,we can see that for the canonical scenario,there can be no enhancement of the transport due to the presence of the enzyme if the ES⇌E~P reaction is much slower than the direct conversion of S⇌P.In the diffusion formalism it is known that the diffusion coefficients of hemoglobin and myoglobin are approximately two orders of magnitude smaller than the diffusion coefficient of oxygen and carbon monoxide,so k±4≪k±1. Therefore,not only will there be no facilitated transport of oxygen in a closed system of this type,but the apparent forward rate will actually be significantly slower than that with no carrier molecules.This is the situation one intuitively considers.Since we know that the ligand is free to flow across the barriers in biophysically relevant systems and,more importantly,that the concentrations of the ligands at the barriers are maintained,we will see how the results from the mathematical model are different in the grand canonical scenario.
1.2 Grand canonical scenario:constant free ligand concentrations
In the grand canonical scenario,the free ligand concentration is held constant in each compartment.Therefore,with the presence of the enzyme,the total amount of the ligand in both the free and bound forms in either compartment,ctotS0and ctotP0,can vary. This is the essence of the problem of facilitated diffusion.In this case,since

we can use the results from King-Altman′s method in Eq.(5) directly.Again,we are interested in the steady-state reaction velocity:
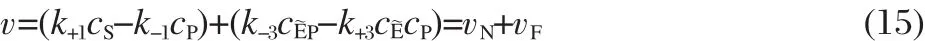
where vNand vFdenote the non-facilitated and facilitated steadystatereaction velocities,respectively.Note that the non-facilitated reaction velocity is the component that is due to direct conversion of the substrate to the product,and the facilitated reaction velocity is the component that is due to the presence of the enzyme in the system.Using Eqs.(2)and(5),we obtain

In the special case where k±4=k±5and k±2=k±3,which is the original system of interest for facilitated diffusion,vFsimplifies to
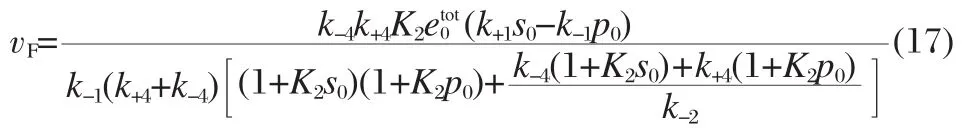
Note that if we assume that k±2≫k±4,as in section 1.1,vFcan be compared with Eq.(24)of Ref.[8]and Eq.(11)of Ref.[10].
The conclusion from the above two sections is that if the system is in the canonical scenario,and k+4≪k+1,k-4≪k-1,then there will be no facilitated transport due to the presence of the protein since the transport mediated byis slow.However,if the system is in the grand canonical scenario,then regardless of whether k±4are large or small,there is an additional transport viaIn this case,facilitated transport occurs.
2 Comparison with Wittenberg′s experimental results
In this section,we will compare the theoretical results from our model with three of Wittenberg′s key experiments.In section 2.1,we will study the facilitation effect of hemoglobin on oxygen as a function of the oxygen partial pressure at the upstream end of the system.Next,in section 2.2,we will examine the effect of increasing the total concentration of the carrier molecules present in the system.Section 2.3 concerns the effect of hemoglobin and myoglobin on the transport of carbon monoxide.In each case,the results from our model suitably reproduce the experimental results.Finally,in section 2.4,we derive a relation between the down-stream ligand concentration,or down-stream partial pressure,and the association-dissociation rates.
We now explain how to compare the theoretical results with the experimental data of Wittenberg[4].We shall determine how the quantities in our model relate to the ligand partial pressures and fluxes reported by Wittenberg.First,we can see that the oxygen and carbon monoxide partial pressures can be equated to our model′s free ligand concentrations using Henry′s Law:

where PP0,PPldenote the ligand partial pressures at the upstream and down-stream ends of the system,and σ is the solubility constant of the ligand studied.According to Ref.[10]and Ref.[22]respectively,the values of σ for Wittenberg′s experimental conditions are:
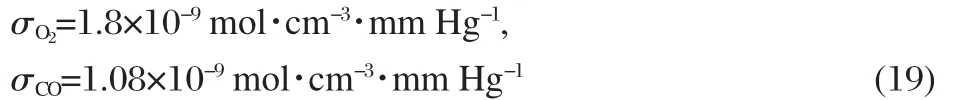
where 1 mm Hg=0.133 kPa.Next,we must convert our steadystate reaction velocity,v,which has units of ligand concentration per time,into a quantity with units moles of ligand diffusing per time,which we will call the total ligand flux,using a scaling factor γ,which is described in the Supporting Information.In order to do this,a conversion factor of a“volume element”will be required.Note that in the comparison between Wittenberg′s experiments and Wymann-Murray′s diffusion theory,a“crosssection area element”was needed.
Finally,we must determine which values to use for the rate constants in our model.The association-dissociation rate constants for oxygen and carbon monoxide combining with hemoglobin and myoglobin are known[4],and can be used directly in our model.The relationship between our transport rate constants and the diffusion of the ligands and enzymes follows from the above mentioned scaling factor.First,we will assume that the diffusion of the ligand,ligand-carrier complex,and carrier is unbiased so that k+1=k-1and k+4=k-4.Then our equation for the total ligand flux,J,in Wittenberg′s units of μL·min-1becomes:
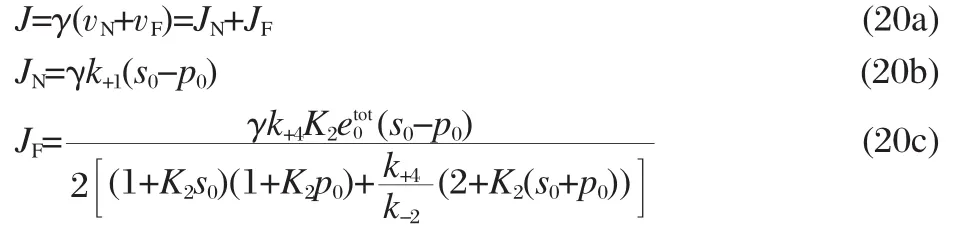
As in the case of the steady-state reaction velocity,the subscript N denotes the non-facilitated component of the total flux and the subscript F denotes the facilitated component of the total flux. Therefore,we will refer to JNand JFas the non-facilitated and facilitated fluxes,respectively.We can see that our theory predicts that the facilitated flux approaches a constant value as the partial pressure at the up-stream end of the system increases,as expected from Wittenberg′s experiments:
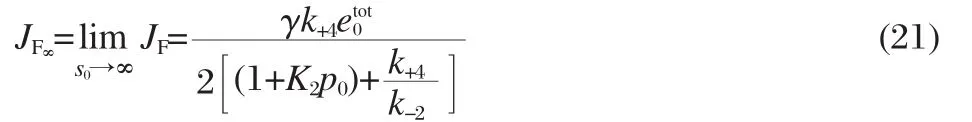
This implies that the total ligand flux approaches a line with slope γk+1as a function of s0.Therefore,we can match the slope of a line fitting Wittenberg′s experimental data points for nonfacilitated fluxes with our theoretical curves to determine a value for k+1.Once we have determined a value for k+1,we can set the value for k+4using the idea that the ratio of the transport rates should be the same as the ratio of the diffusion coefficients:

wheretheDcarrieristhediffusioncoefficient of the carrier molecule, either hemoglobin or myoglobin,and Dligandis the diffusion coefficient of the ligand,either oxygen or carbon monoxide.
Now that we have a method for comparing our theoretical predictionswithWittenberg′sexperimentaldata,wecanproceed.
2.1 Facilitation of oxygen by hemoglobin as a function of oxygen partial pressure
Fig.2 shows a comparison of our theoretical results with Wittenberg′s experimental data using Human Hemoglobin A[4].In this experiment,Wittenberg measured the flux of oxygen through a solution of ferric hemoglobin,to which oxygen does not bind, corresponding to the open circles,and through a solution of hemoglobin,corresponding to the closed circles.The dashed line represents the non-facilitated flux,which is plotted using Eq.(20b)by fitting k+1to the ferric hemoglobin data as described above.In order to take the range of values for the diffusion co-efficients of oxygen and hemoglobin reported in the literature into account,Murray′s values[8]were used to calculate the value of β=DHb/DO2,and three solid curves were generated using Eq. (20a)and the relationships k+4=βk+1,2βk+1,3βk+1,increasing from the lowest to the highest solid curve.The parameter values used to calculate the total and non-facilitated fluxes are reported in the caption of Fig.2.

Fig.2 Oxygen flux vs partial pressure for hemoglobinTheoretical results from our model are compared with Wittenberg′s experimental data[4].The open circles show the flux of oxygen through ferric hemoglobin,which does not react with oxygen.The solid circles show the flux of oxygen through Human Hemoglobin A.The dashed line represents the nonfacilitated oxygen flux,JN,plotted using Eq.(20b).The solid curves,representing the total oxygen flux in the presence of hemoglobin,J,were plotted using Eq. (20a)with k+4=βk+1,2βk+1,3βk+1in increasing order from top to bottom,as discussed in section 2.1.The value of k+1=0.0206 s-1was calculated using the experimental data as described in section 2.Other parameter values were,from Ref.[4]:k+2=3×109cm3·s-1·mol-1,k-2=40 s-1,=1.12×10-5mol·cm-3,p0=0 mol· cm-3,ρ=0.79,A=11.5 cm2;from Ref.[5]:l=2.2×10-2cm;and from Ref.[8]:DHb= 2.45×10-7cm2·s-1,DO2=1.2×10-5cm2·s-1.
Wittenberg reports that the total ligand flux,corresponding to the solid curves,exceeds the non-facilitated flux,corresponding to the dashed curve,by a constant amount for partial pressures at the up-stream end of the system exceeding approximately 2.66 kPa(20 mm Hg).Our model clearly reproduces that result,as we expect from Eq.(21).
2.2 Facilitation of oxygen by hemoglobin and myoglobin as a function of total carrier concentration
Next we can compare our model with Wittenberg′s experimental results concerning the facilitated flux as a function of total carrier concentration,as shown in Fig.3.Wittenberg′s experimental data for hemoglobin and myoglobin are shown as solid and open circles,respectively.The three curves in the main graphs were generated using Eq.(20c)with PP0=99.75 kPa(750 mm Hg)and the same parameters as those in Fig.2,except that the values of DHb,DMbwere calculated using the method described below.
Wittenberg reported that the facilitated flux is proportional to the total carrier concentration for dilute solutions,and decreases at higher concentrations.In our model,the facilitated flux,JF,is linearwiththetotalconcentrationoftheenzyme,etot00,whichmeans that our model can not reproduce Wittenberg′s results without incorporating additional information.This is easily done by allowing the enzyme transport rate,k+4,to depend on the total carrier concentration.Riveros-Moreno and Wittenberg found that the diffusion coefficients for hemoglobin and myoglobin were constant for concentrations less than approximately 6 mmol·L-1(Heme)and decrease for higher concentrations[23].We can fit their data for the diffusion coefficients,shown in the inset graphs in Fig.3,to determine an empirical relationship between the diffusion coefficients and the total carrier concentration.When we allow k+4to vary with increasing etot00according to these relationships,we see that our model qualitatively agrees with the experimental results.Therefore we can conclude that the facilitated flux reaches a maximum value due to crowding of the carrier molecules at higher concentrations.
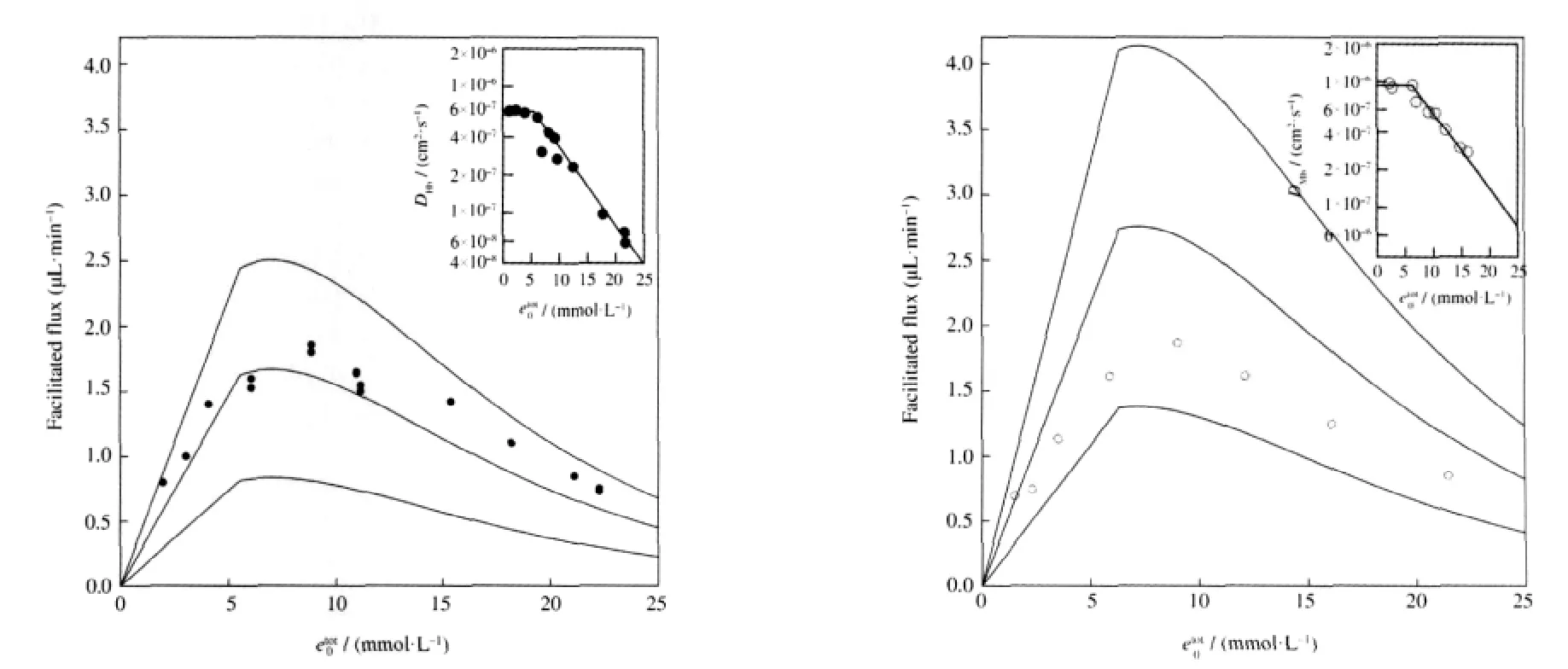
Fig.3 Facilitated oxygen flux vs total Heme concentrationTheoretical results from our model are compared with Wittenberg′s experimental data[4].In each plot,the solid circles represent hemoglobin data and the open circles represent myoglobin data.The solid curves,representing the facilitated oxygen flux,JF,in the presence of hemoglobin or myoglobin,were generated using Eq.(20c)with k+4=βk+1,2βk+1,3βk+1,where the values for DHb,DMbdepend on etot00according to the relationships shown in the inset plots,as described in section 2.2.The partial oxygen pressure at the up-stream end of the system is assumed to be PP0=99.75 kPa(750 mm Hg),and all of the other parameter values are the same as those in Fig.2,with the exception that for myoglobin,k+2=14×109cm3·mol-1·s-1and k-2=11 s-1as in Ref.[4].Inset plots:self-diffusion coefficient vs total Heme concentration. The experimental data points were reproduced from Ref.[23].Curves were fit to the data as described in section 2.2.
2.3 Carbon monoxide facilitation by hemoglobin and myoglobin
Finally,we would like to compare theoretical results from our model with Wittenberg′s experimental results concerning carbon monoxide facilitation by hemoglobin and myoglobin,which can be seen in Figs.4 and 5.Wittenberg′s data for carbon monoxide and nitrogen fluxes are shown as squares and triangles that are solid for solutions containing hemoglobin and open for solutions containing myoglobin.Wittenberg reported that the ratio of nonfacilitated flux of carbon monoxide to the total flux of nitrogen, which is non-facilitated since nitrogen does not react with the carriers,was measured as

The non-facilitated flux is the dashed line through the carbon monoxide data plotted using Eq.(20b)and the value of k+1calculated by matching the slope of the dashed line fit through the nitrogen flux data,multiplied by the conversion factor in Eq.(23). Note that we chose to perform only one fit using both sets of nitrogen data since they seem to coincide.The solid curves in Fig. 4 represent the total carbon monoxide flux using Eq.(20a)and various values for the diffusion coefficients as described in the caption,assuming that there is no back pressure in the experimental setup:PPl=0 kPa(0 mm Hg).The solid curves in Fig.5 are generated in the same way,except we assume that there is a small back pressure of PPl=0.133 kPa(1 mm Hg).
Wittenberg reports that neither hemoglobin or myoglobin enhances the transport of carbon monoxide.Total flux curves plotted for various parameter values,assuming that the back pressure is zero,can be seen in Fig.4.If we use the values from Murray and Wyman[12]then we see no enhancement,which is shown by the solid curves that coincide with the carbon monoxide data in Fig.4.However,other authors report values for the diffusion coefficients under which our model predicts a facilitated carbon monoxide flux of as much as 2.5 μL·min-1for hemoglobin and 1.8 μL·min-1for myoglobin.One notable feature shared by all of the total flux curves in Fig.4 is that the facilitated carbon monoxide flux approaches its maximum value quite rapidly compared to the results for oxygen and hemoglobin,shown in Fig.2.Upon investigation,we find that the facilitated carbon monoxide flux will be nearly abolished if there is a back pressure as small as PPl=0.133 kPa(1 mm Hg)at the down-stream end of the system,regardless of which parameter values are used,as can be seen in Fig.5.We suspect that Wittenberg′s experimental apparatus may not have been capable of keeping the partial pressure at the down-stream end of the system low enough to be able to see any facilitation effect,which is in agreement with the conclusions of Ref.[12].

Fig.4 Carbon monoxide flux vs partial pressure(PPl=0 kPa(0 mm Hg))Theoretical results from our model are compared with Wittenberg′s experimental data[4].The triangles correspond to nitrogen fluxes through hemoglobin(solid)and myoglobin(open),while the rectangles correspond to carbon monoxide fluxes through hemoglobin and myoglobin.In both plots,the lower dashed line fits both sets of nitrogen data,and represents the non-facilitated nitrogen flux since nitrogen does not react with hemoglobin or myoglobin.The upper dashed line represents the nonfacilitated carbon monoxide flux,JN.Each of the solid curves represents the total carbon monoxide flux,J,using Eq.(20a)with parameter values from different authors as described below.The value for the carbon monoxide transport rate,k+1=0.0548 s-1,was calculated as described in section 2.3.In this figure,we assume that PPl=0 kPa(0 mm Hg).Hemoglobin parameters from Ref.[4]:etot00=11×10-6mol·cm-3,from Ref.[22]:k+2=6.75×108cm3·mol-1·s-1,k-2=0.05 s-1;top solid curve,from Ref.[22]:DHb=6.4×10-7cm2·s-1,DCO=1.98×10-5cm2·s-1,middle solid curve,from Ref.[24]:DHb=2.45×10-7cm2·s-1,DCO=1.3×10-5cm2·s-1,bottom solid curve,from Ref.[12]:DHb=2.5×10-7cm2·s-1,DCO=9×10-4cm2·s-1.Myoglobin parameters from Ref.[4]:etot00=8.1×10-6mol·cm-3,k+2=0.5×109cm3·mol-1·s-1,k-2=0.017 s-1; top solid curve,from Ref.[25]:DMb=3.1×10-7cm2·s-1,DCO=0.93×10-5cm2·s-1,bottom solid curve,from Ref.[12]:DMb=4.4×10-7cm2·s-1,DCO=9×10-4cm2·s-1.
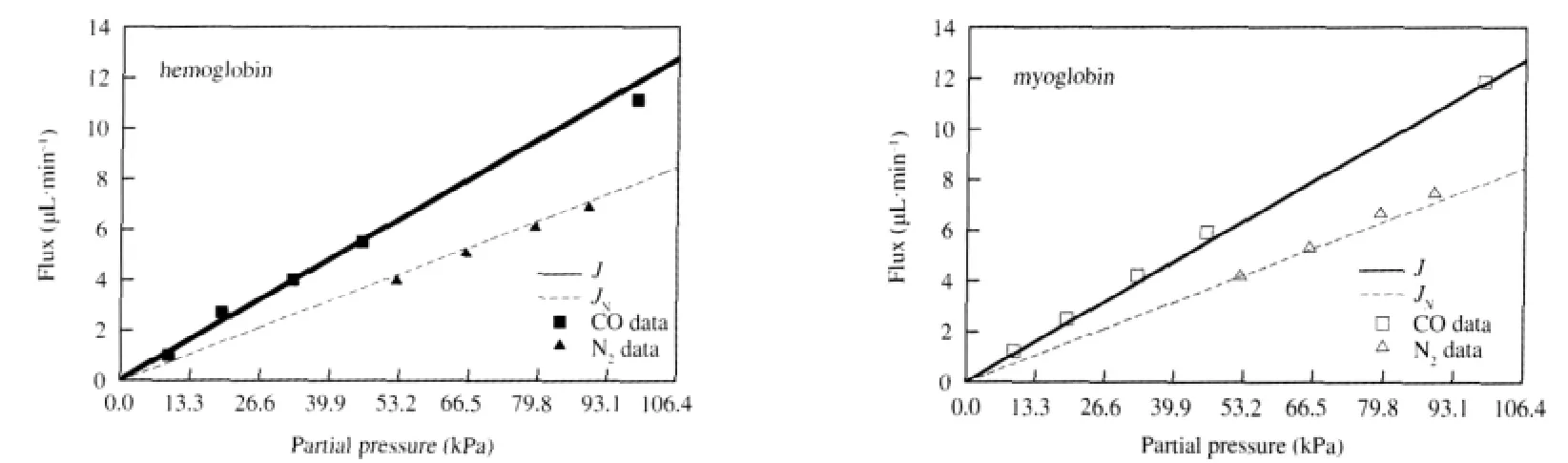
Fig.5 Carbon monoxide flux vs partial pressure(PPl=0.133 kPa(1 mm Hg))These graphs were drawn in the same manner as those shown in Fig.4,with the only difference being that a small back pressure in the system of PPl=0.133 kPa (1 mm Hg)is assumed.Note that in all cases the facilitation is nearly abolished,and each curve is in suitable agreement with the data.
Mochizuki and Forster,using a slightly different setup from that of Wittenberg,were able to measure a facilitation of carbon monoxide by hemoglobin[26].Although Mochizuki and Forster′s methods differed from Wittenberg′s methods,we can use the same parameters and criteria that Nedelman and Rubinow used to compare their reaction-diffusion model[22]with the experimental data.From Fig.2 in Ref.[26],we measure Mochizuki and Forster′s facilitated flux to be JFexp≈0.053 μL·min-1,and our model predicts that JF∞≈0.050 μL·min-1,an excellent agreement(Parameters used:k+2=6.75×108cm3·mol-1·s-1,k-2=0.05 s-1, etot00=6.65×10-6mol·cm-3,s0=4.1×10-6mol·cm-3,p0=s0/2,DCO= 1.64×10-5cm2·s-1,DHb=6.28×10-7cm2·s-1,l=2.45×10-2cm,Aeff= 5.53 cm2,α=1.526×109μL·min-1,k+1as in Fig.5).
These results lead to the observation that the enhancement can be abolished by either taking k-2to be small enough so that the second term in the denominator of JFbecomes dominant,or by setting p0large enough.This suggests that if the dissociation rate is too slow,then the ligand can not escape the carrier molecule fast enough in order to enhance the transport.In other words,the dissociation reaction is rate limiting.Furthermore,if the facilitated flux approaches the maximum value rapidly,even small back pressures in the system will abolish the facilitation effect.
2.4 Back pressure required to abolish the facilitation effect as a function of the reaction rate constants
We can quantify the observation that increasing the back pressure in the system can abolish the facilitation effect by examining the form of JF∞from Eq.(21).First,note that the facilitated flux is the largest when the down-stream free ligand concentration is zero,p0=0 kPa(0 mm Hg),corresponding to the case with no back pressure:
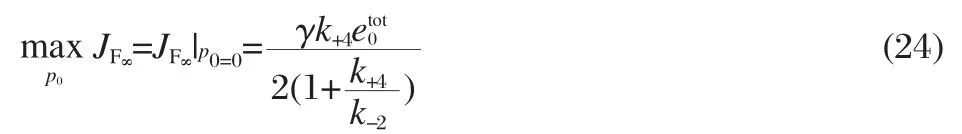
Define p01/2to be the down-stream concentration of the free ligand that decreases the facilitated flux to half of the maximum value:

Note that as long as the transport rate is much slower than the association-dissociation rates,k+4≪k+2,k-2,then p01/2≈k-2/k+2.We can calculate the down-stream partial pressure,or back pressure, required to decrease the facilitated flux to half of the maximum value using Henry′s lawFor the hemoglobin-oxygen system shown in Fig.2,PPl1/2≈0.98 kPa(7.4 mm Hg).For the hemoglobin and myoglobin carbon monoxide systems shown in Fig.4,PPl1/2≈9.31 Pa(0.07 mm Hg)and PPl1/2≈3.99 Pa(0.03 mm Hg),respectively.We can see that the back pressure required to abolish the facilitation of carbon monoxide by either carrier will be orders of magnitude smaller than the back pressure required to abolish the facilitation of oxygen by hemoglobin,making the facilitation effect harder to measure,as we expect from examining Figs.2 and 4.
We can see that a greater affinity for the ligand-carrier binding reaction requires a greater attention to keeping the downstream free ligand concentration,or back pressure,small.Furthermore,we find that a small dissociation rate can have a twofold effect on lowering the facilitation effect:if k-2is small enough,the second term in the denominator of Eq.(20c)can become dominant,diminishing the facilitation,and if k-2is very small, the down-stream ligand concentration,or back pressure,must be maintained at a very low level in order to measure the facilitation effect.
3 Conclusions
Our simple chemical kinetic model reproduces the main experimental and theoretical results and sheds new light on the mechanism behind facilitated transport.We see that the true cause of the enhanced diffusion is that the system is open with respect to the free ligand.The transport is driven by a fixed chemical potential gradient.In other words,every time a free oxygen molecule binds to the carrier molecule at the up-stream end of the system,another free oxygen molecule can enter the cell.Likewise,every time an oxygen molecule dissociates at the down-stream end of the system,a free oxygen molecule must leave the cell.In this way,a facilitation effect is guaranteed given the presence of the carrier molecules in the system.The presence of the carrier molecules creates“parallel pathways”for transport.Furthermore,we find that slow dissociation rates correspond to an increased likelihood that even a small back pressure will abolish the facilitation effect.This conclusion is further supported by Wittenberg′s experimental results that facilitation is not measurable for certain types of hemoglobin that have dissociation rates that are much slower than their association rates, such as Ascaris perienteric fluid hemoglobin[4].In this case the oxygen molecule that binds to the carrier protein can not escape quickly enough compared to the diffusion time scale to produce a facilitation effect.
In summary,we have developed a simple biochemical kinetic model for facilitated transport phenomena.The model is quite general and conceptually simple.One of the advantages of the model is that it can be easily used by researchers.In addition to the formulae we have presented,the system of ordinary differential equations can be easily solved numerically using appropriate parameter values;a situation that may not be the case for the reaction-diffusion model developed earlier.Our model can also easily be extended to situations where more than one ligand is present in the system.
Supporting Information Available:Some of the details that are left out of the main text in the paper have been included.This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.
1 Keener,J.P.;Sneyd,J.Mathematical physiology:cellular physiology,interdisciplinary applied mathematics.New York: Springer-Verlag,1998
2 Fersht,A.Enzyme structure and mechanism.2nd ed.New York: W.H.Freeman and Company,1985
3 Roughton,F.Proc.R.Soc.Lond.B,1932,111:1
4 Wittenberg,J.B.J.Biol.Chem.,1966,241:104
5 Wittenberg,J.B.Physiol.Rev.,1970,50:559
6 Hemmingsen,E.Comp.Biochem.Physiol.,1963,10:239
7 Scholander,P.Science,1965,149:876
8 Murray,J.D.Proc.R.Soc.Lond.B-Biol.Sci.,1971,178:95
9 Wyman,J.J.Biol.Chem.,1966,241:115
10 Rubinow,S.I.;Dembo,M.Biophys.J.,1977,18:29
11 Kreuzer,F.;Hoofd,L.J.Respir.Physiol.,1970,8:280
12 Murray,J.D.;Wyman,J.J.Biol.Chem.,1971,246:5903
13 Murray,J.J.Theoret.Biol.,1974,47:115
14 Fletcher,J.E.Biophys.J.,1980,29:437
15 Meyer,R.A.;Sweeney,H.L.;Kushmerick,M.J.Am.J.Physiol., 1984,246:C365
16 Qian,H.Annu.Rev.Phys.Chem.,2007,58:113
17 Hill,T.L.Linear aggregation theory in cell biology.New York: Springer-Verlag,1987
18 King,E.L.;Altman,C.J.Phys.Chem.,1956,60:1375
19 Hill,T.L.Free energy transduction and biochemical cycle kinetics. New York:Dover Publications,2004
20 Qi,F.;Dash,R.K.;Han,Y.;Beard,D.A.BMC Bioinformatics, 2009,10:238
21 Murray,J.D.Mathematical biology I:an introduction.3rd ed. New York:Springer,2007
22 Nedelman,J.;Rubinow,S.I.J.Math.Biol.,1981,12:73
23 Riveros-Moreno,V.;Wittenberg,J.B.J.Biol.Chem.,1972,247: 895
24 Britton,N.F.Nonlinear Analysis,Theory,Methods&Applications. 1979,3:361
25 Kreuzer,F.;Hoofd,L.Adv.Exp.Med.Biol.,1976,75:207
26 Mochizuki,M.;Forster,R.E.Science,1962,138:897
