障碍物的设置对颗粒流动过程的影响

樊赟赟,王思敬,王恩志

（1.东北大学 资源与土木工程学院,沈阳 110819;2.清华大学 水沙科学与水利水电工程国家重点实验室,北京 100084）

雪崩、滑坡、滚石和泥石流等都是常见的山地灾害,他们非常危险且具有很强的破坏性。近年来在人类活动和气候变化等因素的影响下这些山地灾害发生的频率更加频繁,爆发规模也越来越大。为了减小灾害的危害性除了加强灾害预报,还应该研究灾害发生和发展的规律,判断灾害可能的运动路径及致灾范围,并找到经济而有效的防治方法,这些也将为山区移民规划提供重要的参考和依据[1-4]。

数值模拟是研究山地灾害的一种有效手段,已有许多国内外的学者开展了这方面的研究,并取得了一定的成就[1-17]。雪崩、滑坡、滚石和泥石流等山地灾害的发展过程常常表现出一定的颗粒流动特征,因而可以将这些山地灾害的发展过程以颗粒流动来概化[1-4,10-17]。为讨论方便论文将上述山地灾害发展过程统一视为颗粒流动,通过研究颗粒流动过程的特点来加深对这些山地灾害的认识,并通过研究障碍物设置对颗粒流动过程的作用和影响来探讨如何选用有效而可靠的灾害防治措施方案。

设置障碍物是控制颗粒流动过程的有效手段。研究障碍物对颗粒流动过程的影响,一方面可以通过设置障碍物改变颗粒流动的路径,限制其影响范围,减小其对人类居住环境和基础设施的破坏,以达到防灾和减灾的目的,另一方面也可以充分利用已有障碍物,通过优化设计,得到既合理又经济的防治方案。

近年来国内外学者针对颗粒流动开展了大量的研究,已经形成了多种理论和方法。其中Savage和Hutter较早提出了一定质量颗粒的流动理论具有较大的影响[1-2],理论考虑了由于速度梯度不同而引起的地压系数的变化,能够在正交曲线坐标系下模拟一定质量颗粒的流动,因而得到了比较广泛的关注和研究[1-4,10-16]。同时也有学者比较关注障碍物对颗粒流动过程的影响,他们通过实验和数值模拟讨论障碍物的不同形式和高度等对颗粒流动的影响,并讨论其中的物理过程[3,8,16-17]。

但上述学者均未深入讨论障碍物的不同设置对颗粒流动过程的影响。事实上,在实际的工程应用中障碍物应因循具体的地形和地貌布置,其空间设置将对颗粒流动过程产生较大的影响。该文将应用SH理论,采用Roe格式的有限体积离散方法对流经障碍物的颗粒流动过程进行数值模拟,并讨论障碍物的设置对颗粒流动过程的影响。

1 模型方程[1-2]

SH理论建立了如图1所示的正交曲线坐标系统[3],其中的虚线平面为曲线参考平面,其水平的坡角为ζ,zb为相对参考曲面的底高,理论描述了颗粒材料在垂直于参考曲面上的二维运动。

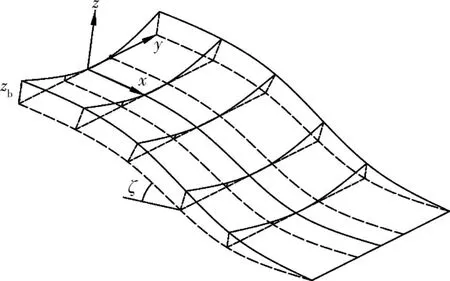
图1 正交曲线坐标系统

式中的无量纲变量h为颗粒流深度,v=（u,v）为深度平均的平行于坡面的平面速度,而u和v则分别是沿坡向和垂直于坡向的平面速度分量,k=-∂ζ/∂x为参考平面的曲率,δ为床面摩擦角,K x和K y分别为沿坡向和垂直坡向的地压力系数。

方程中的无量纲变量能够通过映射变换成原有的物理变量,如式（4）所示：

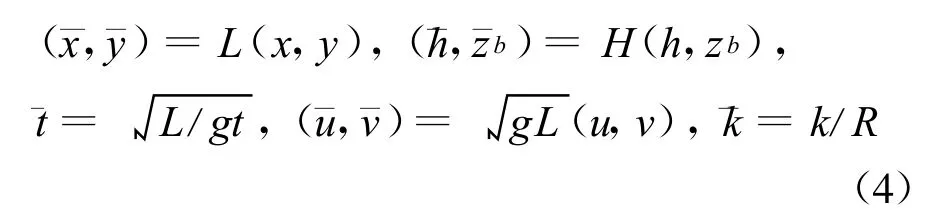
其中g表示重力加速度,H表示颗粒的特征深度,L表示特征长度,R为沟道沿坡向的特征半径,SH理论还定义了2个比值ε=H/L和λ=L/R,他们一般都比较小。

SH理论的一个关键特点就是引入了CM准则的地压力系数,其根据速度梯度条件的不同可以表示为式（5）-（8）,这些关系式在x-y平面剪切比x-z和y-z平面剪切小的条件下是正确的。

式中φ是颗粒材料内摩擦角,而K yact/pass表示主动或被动地压力系数。

对于不同类型的山地灾害,在模化为颗粒流动时,颗粒材料主要由不同的内摩擦角和床面摩擦角来定义。

2 颗粒流经障碍物的过程模拟

2.1 数值方法及计算条件

颗粒流动过程具有复杂性,在大梯度物理参数条件下和颗粒减速堆积或遇到障碍时,流动状态往往会发生变化,因而需要采用稳定而有效的数值方法进行计算模拟。随着现代数值方法的发展,许多优秀的数值方法被应用于SH模型方程的计算中。

论文将以 Roe格式的近似 Riem ann解为基础[18],采用有限体积方式对模型方程进行数值离散,在非结构网格上采用 M USCL（Monotonic Upwind Scheme for Conservation Law s）线性重构方法对空间进行线性重构[19],用 Rung-Kutta方法[20]获得具有时空二阶精度的格式,对界面插值进行限制以避免出现假振[21],并对与速度有关的摩擦阻力项用半隐式的方法离散[22]。

为便于比较分析,选用文献[3]所用的计算模型条件,研究障碍物的不同设置对颗粒流动过程的影响。

如图2所示,假定在半椭球形容器下有一定质量的颗粒材料。颗粒材料在40°的坡面上被突然释放,经过一段光滑的曲面运动到水平面上。计算范围取为沿坡向方向x=[0,30],垂直于坡向方向y=[-10,10]。曲面的坡角可以表示为：

其中椭圆中心坐标（x0,y0）=（5,0）,椭圆长轴a=4,椭圆短轴b=2,颗粒材料的最大初始高度hinimax=1。计算模型中的参数取为：颗粒内摩擦角 φ=35°,床面摩擦角 δ=30°,特征比值 λ=1,ε=1。

假定颗粒粒径相对障碍物足够小,则当颗粒连续的流经障碍物后,将形成不同的堆积,而颗粒粒径的差别则综合体现在内摩擦角和床面摩擦角中。文献[3]在以上的初始条件下计算并讨论了障碍物的不同高度对颗粒流动过程的影响,研究发现只有当障碍物足够高时才能在堆积区形成无颗粒堆积的“安全区域”。因而,该文选取能够形成“安全区域”的障碍物高度H=5进行计算和讨论,障碍物则选择具有代表性的四面体障碍物。

图2 计算模型条件示意图

2.2 颗粒流经朝向上坡障碍物的过程模拟

设置关于坡面对称的四面体障碍物,障碍物的底面是边长为4的正三角形,令它的一个顶点朝向上坡,该顶点的对边位于x=17（如图2中实线所示）。在计算中,不考虑障碍物的变形作用,通过改变地形条件实现四面体障碍物对颗粒流动过程的影响。对该条件下的颗粒流动过程进行计算模拟,得到了在不同时刻下的颗粒流深度等值线图,如图3所示（等值线间距为0.05）。

从图3结果中可以看到,颗粒材料在重力作用下开始向x和y方向流动,且沿坡向方向流动较快（t=3）。当颗粒到达障碍物时,由于障碍物的作用,颗粒的流动方向发生了改变,颗粒开始分别向2个方向流动（t=6）,并且在重力作用下继续加速流动（t=9）。当颗粒到达水平面,前部的流动开始减速形成堆积,但尾部的流动仍在加速（t=12～18）,直到尾部也到达堆积区（t=21）。颗粒材料最终在水平面上堆积形成了两个对称的颗粒堆（t=24）,由图中可见,由于障碍物的作用,在对称的颗粒堆中间形成了一个没有颗粒堆积的“安全区域”。由此可见,障碍物改变了颗粒流动的路径,并影响了其最终的堆积形态。在正确的设置条件下形成了没有颗粒流动和堆积的“安全区域”,其可以看做是为避免灾害破坏的实际可行的应用区域,这对灾害防护的设计具有重要的意义。

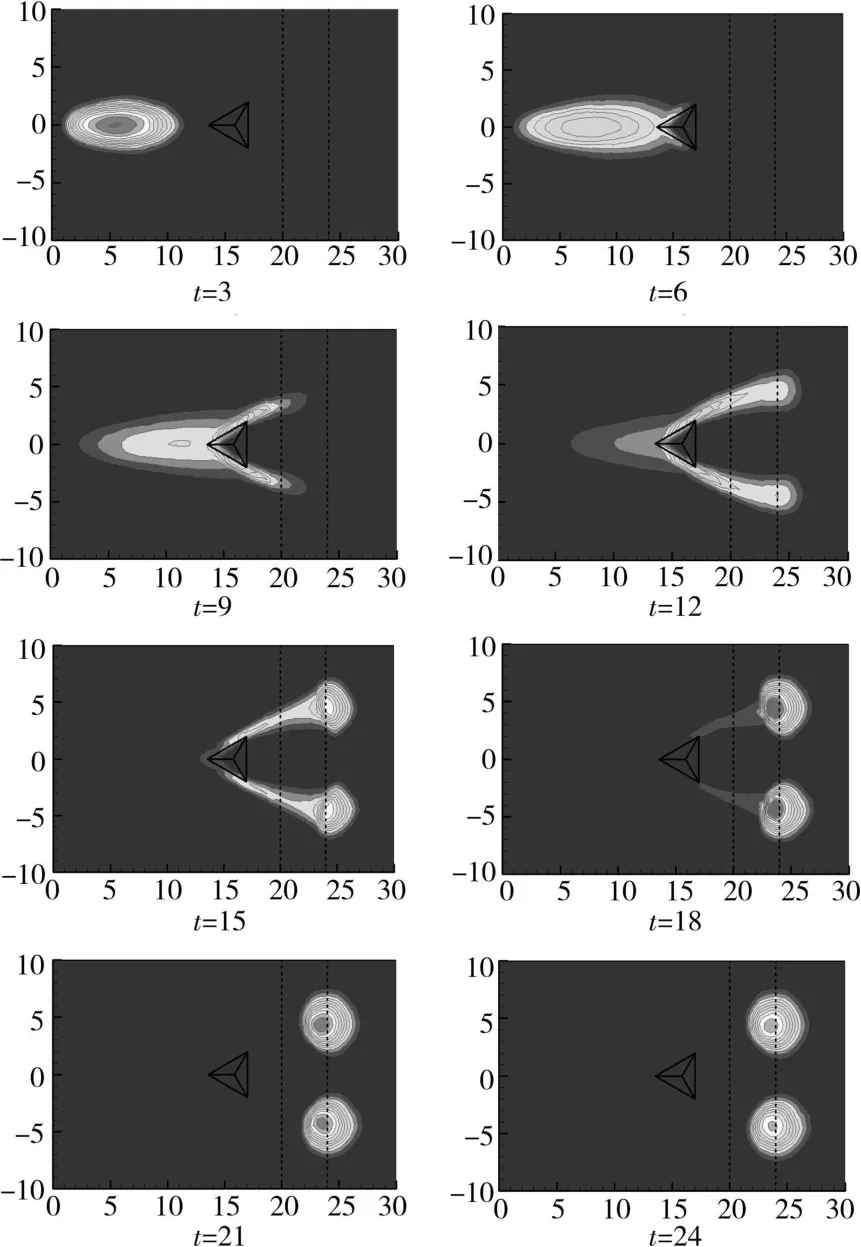
图3 颗粒流经朝向上坡障碍物的过程

值得一提的是,虽然所用的数值方法不同,但图3的模拟结果与文献[3]中的相关结果相同,这也验证了本文数值方法的有效性。

2.3 颗粒流经朝向下坡障碍物的过程模拟

为了比较研究障碍物的不同角度设置对颗粒流动过程的影响,将朝向上坡的障碍物沿垂线旋转180°得到了朝向下坡的障碍物（如图2中虚线所示）。对颗粒流经朝向下坡障碍物的过程进行计算模拟,得到了颗粒流动发展过程中不同时刻的颗粒流深度等值线图,如图4所示（等值线间距为0.05）。

图4 颗粒流经朝向下坡障碍物的过程

从图4结果中可以看到,颗粒材料在遇到障碍物前的运动与图1中的计算是一致的（t=3）,当颗粒到达障碍物时,由于障碍物的阻碍作用,前部的颗粒爬上障碍物（t=6）,并在运动到一定的高度后从障碍物的两侧流下（t=9）,颗粒被障碍物分开为2部分,这2部分到达水平面后开始减速（t=12）,在水平面上逐渐形成了两个对称的颗粒堆（t=12～21）,并在t=24时颗粒堆积基本完成。与设置朝向上坡障碍物的结果相比,由于角度设置不同,朝向下坡的障碍物截留了部分颗粒,并且由于障碍物的截留作用水平面上的两个颗粒堆变小,在2个颗粒堆中间形成有无颗粒堆积的“安全区域”,但也因朝向下坡的障碍物缺乏良好的分导作用而较小。由此可见,障碍物的不同角度设置将对颗粒的流动过程产生重要的影响。

颗粒流经朝向下坡障碍物过程中的这些特点已经被相关的试验所证实[8]。

2.4 障碍物的位置设置对颗粒堆积的影响

在实际的工程中,障碍物往往需要根据地形地物条件以及防治的需要进行布置。这时障碍物的布置不再像前面讨论的2种典型过程那样具有对称性,障碍物的位置设置将会对颗粒流动过程及最终的堆积形态产生影响。因此讨论障碍物的位置设置对颗粒流动和堆积过程的影响,研究其中的变化规律对于优化防灾工程设计和山区规划设计是很有意义的。

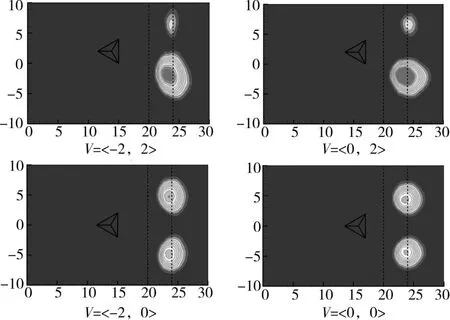
图5 障碍物位置设置对颗粒堆积的影响

在相同的计算条件下将3.2节中所讨论的朝向上坡的障碍物在计算平面上平移向量V,得到4种不同的障碍物布置。在不同的障碍物布置条件下进行计算,分别得到了各自的颗粒流动过程,他们均在t=24时基本完成了堆积,堆积等值线如图5所示（等值线间距为0.05）。

从图5结果中可以看到,颗粒在流经不同位置的障碍物后,均在障碍物的下游形成了2个颗粒堆,且在2个颗粒堆的中间形成了一个没有颗粒堆积的“安全区域”。障碍物沿坡向（x方向）的不同位置设置影响了“安全区域”的范围和颗粒堆的形态,这是由颗粒流动中不同的能量消耗过程引起的,障碍物沿垂直坡向（y方向）的不同位置设置则显著的影响了两个颗粒堆的质量分配,同时“安全区域”具有与障碍物相同的位移趋势,体现出障碍物对坡下的保护作用。

3 结论

雪崩、滑坡、滚石和泥石流等都是常见的山地灾害,他们的发展具有很强的破坏性,对人类的生命和财产安全构成了严重的威胁。为防治和减小灾害,就必须加强对灾害运动特征和防护措施的研究。

这些山地灾害具有颗粒流动的运动特点,因而可以采用颗粒流动的相关理论对其运动过程进行研究。论文采用了模拟颗粒流动的SH理论和Roe的有限体积离散格式对颗粒流经障碍物的过程进行了数值计算,模拟了在不同障碍物设置条件下的颗粒流动过程,研究了不同的障碍物设置对颗粒流动和堆积过程的影响。

数值模拟的结果表明在颗粒流动路径中设置障碍物可以改变颗粒流动的方向,在障碍物高度足够的条件下,会在障碍物的下坡方向形成一个没有颗粒堆积的“安全区域”,其可以看做是为人居环境和基础设施免遭灾害破坏的实际可行的应用区域,对灾害防护的设计具有重要的意义。但是障碍物的不同设置会影响颗粒流动和堆积的过程,为了达到防护的目的,障碍物的设置一定要合理。

在实际的工程设计中地形地物条件更加复杂,结合数值模拟的方法可以对防治障碍物的设置进行优化设计,从而得到经济而合理的防治措施方案,为山区灾害防护和移民规划提供重要的参考和依据。

[1]SAVAGE S B,HUTTER K.The motion o f a finite mass of granular material down a rough incline[J].Journal of Fluid Mechanics,1989,199：177-215.

[2]SAVAGE S B,HUTTER K.The dynam ics of avalanches of granular materials from initiation to runout.I：Analysis[J].A cta Mechanica,1991,86（1-4）：201-223.

[3]CH IOU M C,WANG Y,HUTTER K.In fluence of obstacles on rapid granu lar flow s[J].A cta Mechanica,2005,175（1-4）：105-122.

[4]IVERSON R M,DENLINGER R P.Flow of variably fluidized granular masses ac ross three-dimensional terrain：1.Coulomb m ixture theory[J].Journal of Geophysical Research,2001,106（B1）：537-552.

[5]王纯祥,白世伟,江崎哲郎,等.基于 GIS泥石流二维数值模拟[J].岩土力学,2007,28（7）：1359-1368.

W ANG CHUN-XIANG,BA ISH I-WEI,ESAKI T,et al.GIS based tw o dimensional numerical simulation of debris flow[J].Rock and SoilMechanics,2007,28（7）：1359-1368.

[6]李珂,唐红梅,易丽云,等.泥石流沟岸耦合三维数值仿真[J].重庆建筑大学学报,2008,30（1）：68-76.

LI KE,TANG HONG-MEI,YI LI-YUN,et al.Numerical simulation on coup ling problem betw een debris flow and bank of debris flow va lley[J].Journal of Chongqing Jianzhu University,2008,30（1）：68-76.

[7]李同春,李杨杨,章书成,等.泥石流泛滥区域数值模拟[J].水利水电科技进展,2008,28（6）：1-4.

LI TONG-CHUN,LI YANG-YANG,ZHANG SHUCHENG,etal.Numerical simu lation on inundation area of debris flow[J].Advances in Science and Technology of Water Resources,2008,28（6）：1-4.

[8]马宗源,张骏,廖红建.黏性泥石流拦挡工程数值模拟[J].岩土力学,2007,28（s1）：389-392.

M A ZONG-YUAN,ZHANG JUN,LIAO HONGJIAN.Numerical simulation o f viscous debris flow b lock engineering[J].Rock and SoilM echanics,2007,28（s1）：389-392.

[9]HUNGR O.Numerical modelling of the motion of rapid,flow-like landslides for hazard assessment[J].Ksce Journal o f Civil Engineering,2009,13（4）：281-287.

[10]鲁晓兵,王义华,王淑云,等.碎屑流沿坡面运动的初步分析[J].岩土力学,2004,25（S2）：598-600.

LU XIAO-BING,WANG YI-HUA,WANG SHUYUN,et al.The Primary analysis on the castic gain flow[J].Rock and Soil M echanics,2004,25（S2）：598-600.

[11]YU B,DALBEY K,WEBB A,etal.Numerical issues in com puting inundation areas over natural terrains using Savage-Hutter theory[J].Natural H azards,2009,50（2）：249-267

[12]KALAND C,STRUCKMEIER J.A kinetic scheme for the savage hutter equations[J].M athematicalMethods in the App lied Sciences,2008,31（16）：1922-1945.

[13] BOUCHUT F, FERNANDEZ NIETO E D,MANGENEY A,et al.On new erosion models of Savage-Hutter type for avalanches [J].A cta Mechanica,2008,199（1-4）：181-208.

[14]PUDASA IN IS P,HUTTER K.Rapid shear flow s of d ry granu larmasses down curved and twisted channels[J].Journalof Fluid Mechanics,2003,495：193-128.[15]WANG Y,HUTTER K,PUDASA INI S P.The Savage-Hutter theory：a system of partial differential equations for avalanche flow s o f snow,debris and mud[J].Journal of App lied M athematics and Mechanics,2004,84（8）：507-527.

[16]GRAY JM N T,TA IY C,NOELLE S.Shock w aves,dead zones and particle-free regions in rapid granu lar free-surface flow s[J].Journal o f Fluid Mechanics,2003,491：161-181.

[17]TEUFELSBAUERH,WANG Y,CH IOU M C.Flowobstacle interaction in rapid granu lar avalanches：DEM simu lation and comparison with experiment[J].Granular Matter,2009,11（4）：209-220.

[18]ROE P L.Approximate Riemann so lvers parameter vectors and difference schemes[J].Journal of Computational Physics,1981,43（2）：357-372.

[19]OSHER S.Convergence of generalized MUSCL schemes[J].Siam Journal of Numerical Analysis,1996,22（5）：947-961.

[20]HUBBARD M E.Mu ltidimensional slope limiters for MUSCL type finite volume schemes on unstructured grids[J].Journal of Com putational Physics,1999,155（1）：54-74.

[21]DARW ISH M S,MOUKALLED F.TVD schemes for unstructured grids[J].International Journal of Heat and Mass Transfer,2003,46（4）：599-611.

[22]BRUFAU P,GARCíA-NAVARRO P,VáZQUEZCENDóN M E.Zero mass error using unsteady wetting-drying conditions in shallow flows over dry irregu lar topography[J].International Journal for Numerical Methods in Fluids, 2004,45（10）：1047-1082.

（编辑王秀玲）