基于BP神经网络的大跨桥梁结构混凝土温度预测

田 谷,续若楠,缪长青,孙传智

(东南大学 土木工程学院,江苏 南京210096)

0 引 言

在现代桥梁工程的建设中,越来越多的工程研究表明大体积混凝土中的温度变化的重要性。混凝土浇注后,水泥与水结合发生水化作用,同时也是混凝土的凝固过程。随着水化热的逐渐减少及热量的散发,混凝土的温度就会慢慢地降低。桥墩施工中的混凝土大都体积庞大,其温度在浇筑后3 d～5 d内呈上升趋势,以后温度逐渐下降,一般经过较长时间才能达到稳定温度。在这个过程中,水泥水化作用要生成大量的热量,由于混凝土自身的热物理性能和外界不同情况下的气温状况,形成不同的温度分布,构成整个桥墩的温度场。由于温度场分布的不均匀,内外形成温差以及表面和外界形成温差,温差的存在产生温度热应力.如果该温度应力超过混凝土的拉应力,将可能产生裂缝[1]。

我国的《公路桥涵施工技术规范》(JTJ041-2000)关于大体积混凝土的定义是:现场浇注的最小边界尺寸为1m～3 m且必须采取措施以避免水化热引起的温差超过25℃的混凝土称为大体积混凝土。美国的混凝土学会ACI的规定为:“任何就地浇注的混凝土,其尺寸之大,必须得采取措施解决其水化热及随之引起的体积变形问题,以最大限度减少开裂”。关于大体积的混凝土的定义国内外不尽相同,在大体积混凝土浇筑过程中的温度场分布是一种非常复杂的高度非线性映射关系,结构断面尺寸、外界气温、水泥配合比、结构内部温差以及结构自身特点等都会影响混凝土浇筑与控制方法,并影响结构最终应力。因此需要综合考虑各种影响温度变化的因素予以确定[2,3]。

本文利用人工神经网络理论从反问题的角度用多组影响因素数据和温度值训练出能够描述温度场的网络,简化了原本复杂的求解过程,此神经网络对大体积混凝土的温度控制起一定的指导作用。

1 应用BP神经网络预测混凝土水化热温度

1.1 工程背景

瀛洲大桥结构共分为三个部分,主桥中跨为跨径120 m带悬臂刚架的中承式钢管混凝土系杆拱桥(如图1所示),主桥边跨为3 m×50 m带悬臂半孔的无推力上承式钢筋混凝土箱型拱桥,两岸引桥为预应力钢筋混凝土连续箱梁结构。在正常使用阶段,刚架系杆拱是超静定结构,桥梁上部、下部以及基础甚至地基连成一体,结构的超静定次数较多,受力十分复杂。系杆拱拱墩固节点的构造较为复杂,拱肋、桥墩、帽梁汇聚在这里,一般为不规则的几何体。固节点处的受力很复杂,各方向的力都集中于此点,且受系杆强大的集中力作用,容易在主拉应力方向发生开裂。另一方面,瀛洲大桥拱肋2位于主跨侧,根部厚度2m,高度3.5m,横向长度为20 m,底板和顶板厚度为0.5 m,中腹板厚度为0.6 m,边腹板厚度为0.699 m～0.954 m,中心隔板宽为4 m,厚度为2.5m,因此此处拱肋具有了明显的大体积混凝土结构特点,本文选择的三角区桥跨内侧拱肋为研究对象,如图1所示。

图1 瀛洲大桥结构主跨示意图

1.2 BP神经网络的参数选择

导热系数、计算厚度这两个参数与混凝土的温度和环境温度有着很大的关联。根据混凝土温度场的分布规律,笔者认为:当结构的尺寸一定时,虽然混凝土材料、外界环境温度、和导热性能是影响某点混凝土的主要因素,但是某点温度的变化情况、最大值、与外界温差主要和此点的位置以及入模温度相关。

大量工程实践表明,混凝土内部的实际水化热温升与每m3的水泥用量,结构计算厚度,混凝土的热性能,入模温度和环境温度有关。根据现场埋设的温度传感器,可以量测混凝土水化热温度的变化情况。选择单位体积混凝土发热量、导热系数、计算厚度、浇筑入模温度和外界温度等5个参数作为BP网络的输入参数,来进行训练样本。

国内大体积混凝土工程一般的温度计算都是计算混凝土的中心最高温度Tmax及表面温度Tb,本文为了更突出且简便地反映混凝土水化热对位置不同的测点的温度影响,因此选择训练样本的三维坐标和入模温度作为输入参数,输出参数为各样本的温度随时间变化值,隐层的神经元数目为10[4,5]。

鉴于现场测试点较少,且只集中在两个截面上,故提取有限元仿真结构作为输出值,图2为瀛洲大桥拱肋的尺寸示意图。输出值第1 d每隔3 h取1次值,第2 d、3 d每6 h取1次值,第4 d、5 d每12 h取1次值、第6 d～10 d每1 d取1次值,图3为拱肋的有限元模型。

图2 拱肋2尺寸示意图

1.3 BP神经网络的训练样本

本文采用拱肋中心部分水化热温度变化值作为所研究对象,样本点位置如图4所示,共34个点数据作为训练样本(●表示),样本输入参数如表1。神经网络预测的温度结果用4个点作为检验样本(▲表示)。训练样本点与检验样本点位置如图4所示。

图3 拱肋的有限元模型

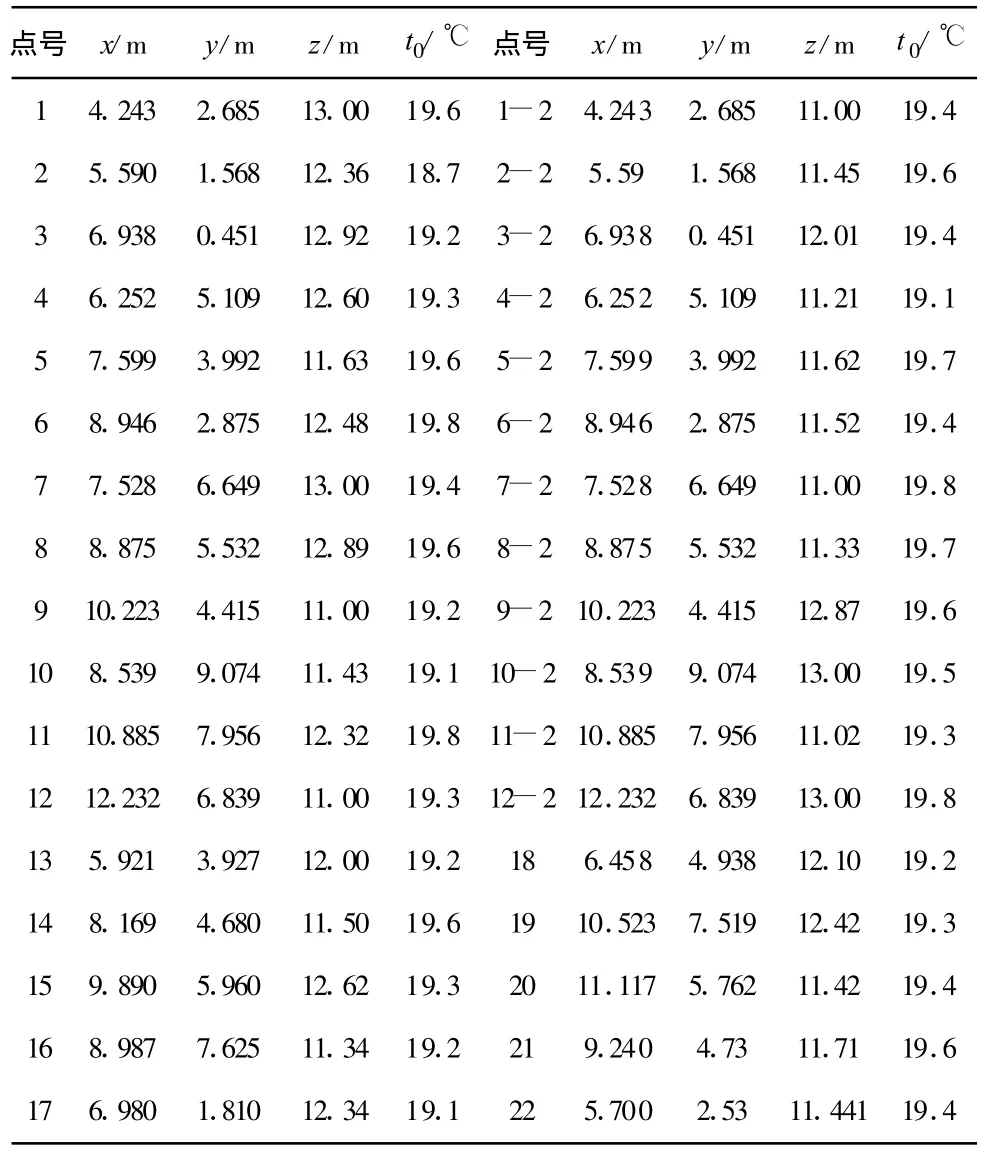
表1 样本输入参数

图4 样本点位置示意图

1.4 BP神经网络的训练及检验

把训练向量输入BP神经网络模型,利用MATLAB中的neural network中的NNTOOL进行训练。网络共进行了1 047次训练,收敛于全局最小点。最后,应用Sim()函数进行仿真和检验。检验选择结构中4个点的温度数据作为检验样本,4个检验样本的输入参数如表2所示。正常坐标下的最终逼近曲线如图5所示,有限元仿真与神经网络预测的温度变化曲线如图6～图9所示[6～9]。

表2 验证样本

图5 正常坐标下的最终逼近曲线

图6 样本1预测结果与有限元结果对比图

图7 样本2预测结果与有限元结果对比图

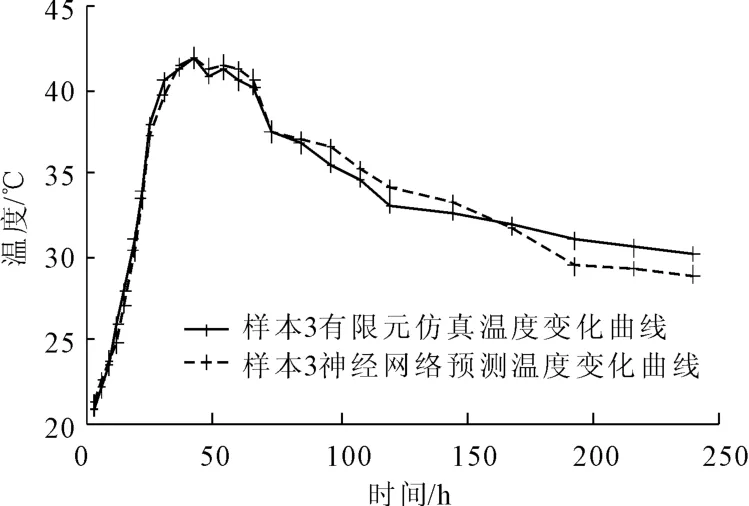
图8 样本3预测结果与有限元结果对比图

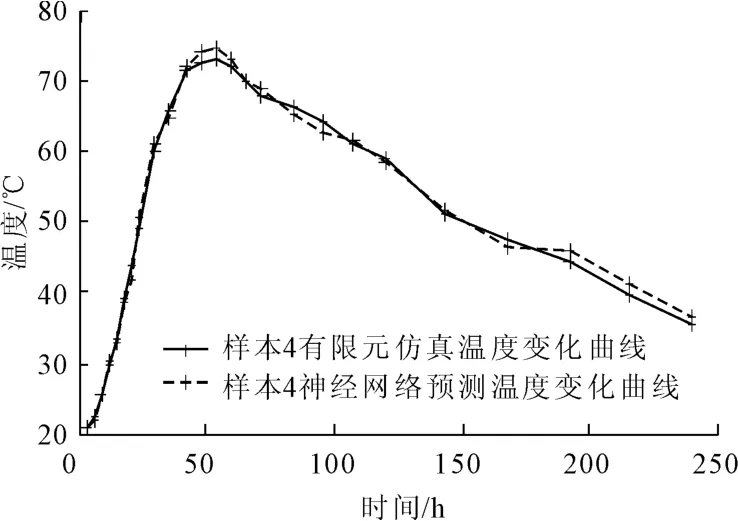
图9 样本4预测结果与有限元结果对比图

从以上数据对比中可以发现,BP神经网络的预测结果总体上与有限元仿真结果相差不大,样本1～样本4的平均误差分别为-1.02%,0.64%,-0.38%,0.52%,最大误差值分别为-4.8%,5.8%,-5.2%,5.3%,最大误差值发生的时间分别在浇筑后192 h,120 h,192 h,216 h。

由于样本点1和样本点4处于拱肋结构的内部,在混凝土浇筑后45 h～50 h,水化热引起这两点的最高温度达到最大值(＞70℃),此时神经网络预测的温度值平均误差分别为-0.2%和1%;样本点2和样本点3位于拱肋的边界,受外界环境温度影响比较明显,在混凝土浇筑后30 h～45 h,水化热引起这两点的最高温度达到最大值(＜42℃),神经网络预测的温度值平均误差为1%和0.4%。

由此看出,利用此BP神经网络预测大体积混凝土浇筑后水化热产生的温度峰值和最大温差梯度是可以应用于工程实践的。

2 结 语

控制大体积混凝土水化热阶段的裂缝开展,必须首先对其进行温度监控,继而考虑温度效应对早期结构的不利影响,从而采取降低水化热的放热量及其反应速率,调整内外温差峰值等方法提高早期强度,防止早期裂缝。通过工程实例分析表明利用BP人工神经网络能够较准确地对桥梁的大体积混凝土水化热时的温度场进行预测,并可以通过训练确定适应效果最优的BP人工神经网络,在此基础上结合有限元分析,影响参数的修正和温度效应的计算能得到与工程实际更加吻合的结果[10]。

[1] 赵秀云.桥梁大体积混凝土裂缝产生原因与防治措施[J].中国新技术新产品,2009,(15):52.

[2] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,2001.

[3] 吕建福.大体积混凝土温度应力场与开裂的研究[D].哈尔滨:哈尔滨工业大学,2005.

[4] 王旭,王 宏,王文辉.人工神经元网络原理及应用[M].沈阳:东北大学出版社,2003.

[5] 邓 磊.基于神经网络的桥梁承台混凝土温度预测系统研究[D].武汉:武汉理工大学,2006.

[6] 虞和济,陈长征,张 省,等.基于神经网络的智能判断[M].北京:冶金工业出版社,2000.

[7] 董长虹.Matlab的神经网络与应用[M].北京:国防工业出版社,2005.

[8] 许 波,刘征.Matlab工程数学应用[M].北京:清华大学出版社,2000.

[9] 王新刚,王启才,周 岩,等.基于人工神经网络的大体积混凝土温度场预测[J].混凝土,2006,(9):21-24.

[10] 韦爱凤.大体积混凝土裂缝控制的有效措施[J].广西工学院学报,2000,(2):20-23.