基于FEPG的三线圈系动态问题求解
2010-02-06张妙瑜
张妙瑜
(西安石油大学电子工程学院 陕西西安)
基于FEPG的三线圈系动态问题求解
张妙瑜
(西安石油大学电子工程学院 陕西西安)
基于有限元程序自动生成平台FEPG,建立了三线圈系动态问题两个未知场的有限元控制方程,通过编写元件化程序,对阵列感应测井仪器在地层运动的响应进行了求解,实现了对其动态问题的透明计算。结果表明该方法可以用于二维电磁场问题计算,为研究三维时谐电磁场问题,开发出更多地层模型的测井响应数值计算软件奠定了基础。
三线圈系;电磁场;有限元控制方程;FEPG
0 引 言
有限元方法是50年代随着电子计算机的发展而发展起来的一种求解偏微分方程的数值计算方法[1]。它是当今求解偏微分方程最有效的数值方法,其原理是基于微分方程弱解形式(即力学中的虚位移原理)。由于它通用性强、使用广泛,作为具有巩固理论基础和广泛应用效力的数值分析工具,很快成为各个学科领域与各种生产部门,尤其是高新技术产业普遍采用的工程与科学计算方法[2]。
目前出现的通用有限元软件并不通用,只能求解很少的一部分有限元问题,不公开源代码,纯黑箱操作,对用户来说程序是不可改动的,极大地限制了用户的创造性。而有限元程序自动生成系统FEPG(Finite Element Program Generator),适用于求解各种领域的各种工程与科学的有限元问题,本文通过数学公式推理的方式,建立FEPG所需的微分方程表达式和算法表达式,对三线圈系阵列感应测井仪器在旋转对称地层中电磁场分布进行求解,从而编程实现了对地层电磁场动态问题的透明计算。
1 有限元程序自动生成软件FEPG设计思想
对于一个有限元问题的描述主要是两方面的内容:一方面是物理模型的描述,在数学上可归结为偏微分方程表达式;另一方面是给出求解区域和边界条件,统称为几何建模。FEPG系统是基于虚位移原理(即弱形式)而不是变分原理,要求用户将物理模型书写成弱形式的微分方程表达式,然后利用有限元语言来描述该物理模型。它把完整的有限元程序分解为可变部分和不可变部分。不变部分系统直接给出,可变部分是根据方程和算法用有限元语言描述,通过生成系统自动产生,然后可变部分和不变部分组成完整的有限元程序,如图1所示。每个元件程序都是一个完整的FORTRAN程序,可以单独进行编译、连接与运行,它们之间的通信完全通过磁盘文件[2]。
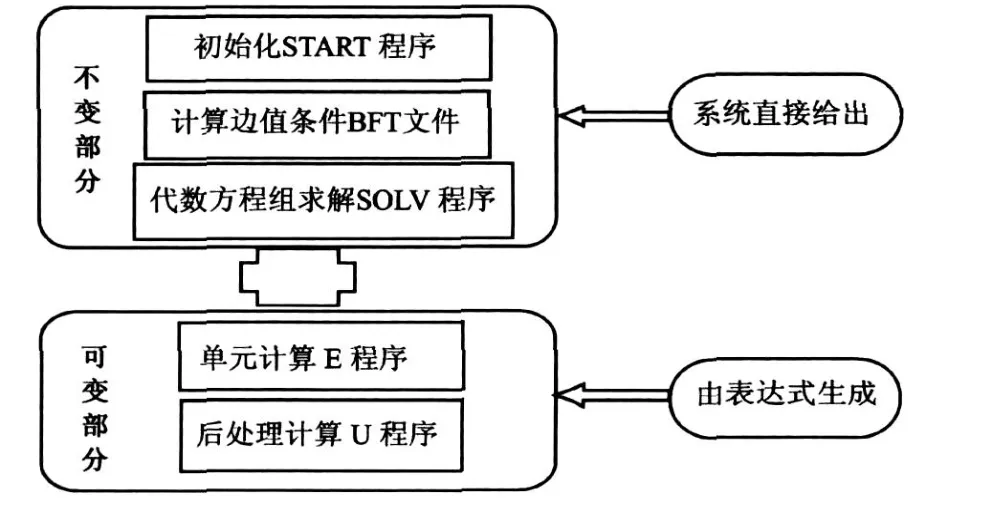
图1 有限元程序自动生成示意图
用户需要给出三种类型的文件:一种是描述有限元控制方程的PDE文件,由这些文件自动生成计算单元刚度矩阵、单元阻尼矩阵和单元载荷向量等单元子程序;再一类是GCN文件,给出多场问题中单场问题的算法来形成多场问题的算法,同时给出各物理场之成系统可由这些表达式自动生成全部的间的耦合方式以及求解流程;最后一类是GIO文件,给出各个物理场的PDE文件名以及求解区域的体单元类型信息及坐标系名。有限元程序自动生有限元程序,突破了国内外的通用有限元软件只适用于特定领域和特定问题的限制。对电磁场分布来讲,在通用软件中研究其本构模型是不可能的,但利用该平台,用户可以使用自己的本构模型[2]。
2 三线圈系阵列感应测井仪器电磁场分布的有限元控制方程
2.1 电磁学基本方程
感应测井工作频率为20 kHz,电磁波在地层中的趋肤深度一般在1 m~10 m范围内,因此严格的感应测井理论是建立在Maxwell方程的基础之上,它是感应测井电磁场理论的基础[3]。
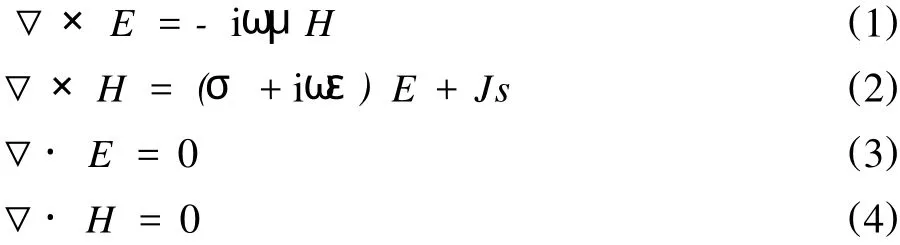
Maxwell方程[4]在测井问题中很有用,感应测井的场源是单一频率并随时间作正弦变化。即使不是单一频率的正弦变化场,也可分解为基波和高次谐波的场的叠加。这里的电磁场源为电流源,JT=ITδ(r-a)δ (z-zs)φ^,φ^为单位矢量,是圆柱坐标系(r,φ,z)中的φ方向;zs是发射线圈的纵向位置;a是线圈缠绕的芯棒半径。
2.2 地层模型
三线圈系阵列沿井眼运动,如图2所示,记录每个深度点的测量信号(接收电压)。三线圈系中,T是发射线圈;R是接收线圈,接收来自地层各部分的信号; B是屏蔽线圈。那么建立的地层模型为纵向3层、径向4层[5]。
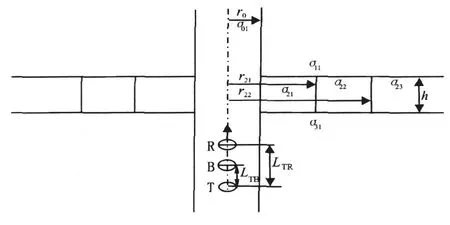
图2 地层模型示意图
2.3 耦合场的有限元控制方程
下面在基本方程(1)~(4)基础上,利用虚位移原理和最小二乘法建立三线圈系动态问题求解的有限元控制方程。二维时谐磁场微分方程向量形式为[6]
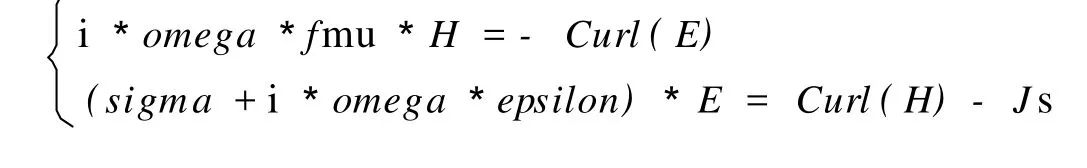
其中,H为磁场强度向量,E为电场强度向量,i为复数单位,omega为角频率常数,fmu为磁导率, sigma为电导率,epsilon为介电常数,Js为源电流密度。
由上面得第一个方程有:
H=-Curl(E)/(i*omega*fmu)
代入第二个方程可得微分方程的弱形式为[7]:
[(i*sigma - omega*epsilon) *E;E] + [1/(fmu*omega)*Curl(E);Curl(E)]=i*|n*H;E|-[i*Js;E]
其中,[· ; ·]表示区域上的两个函数或表达式的内积,“;”表示虚位移,也就是说“ ;”后面的表达式中出现的未知函数表示该函数的变分。|·;·|表示区域边界上两个函数或者表达式的内积,“ ;”表示虚位移,也就是说“ ;”后面的表达式中出现的未知函数表示该函数的变分。n表示区域边界上外法向单位向量,n*H表示叉乘。
在二维问题中,我们只需求解 Ez(即 E的z向分量),即可求电场强度 Hx,Hy。
2.4 求解结果
图3为剖分后的网格图,网格节点数为24 779。图4为第132个采样点的电场强度实部云图。图5为串行计算测井响应的散点图,由图5可知,其响应基本反映原状地层的性质,由于受地层非均质影响以及网格剖分的限制,曲线在层界面有波动,因而曲线实际反映的是仪器周围整个地层的综合响应。

图3 网格图
3 结 论
三线圈系阵列感应测井仪器在旋转对称地层中的电磁场分布在感应测井响应研究中处于核心地位。本文依据麦克斯韦方程建立电场及磁场的有限元控制方程,通过实施编程,对电场强度和磁场强度进行了分析计算。该程序克服了一般通用有限元软件的黑箱模型,其结果与实际地层响应基本一致。目前斜井和水平井钻井逐渐成为主流,因此,有必要在此基础上,开发出更多地层模型的测井响应数值计算软件。

图4 第132个采样点的电场强度实部云图
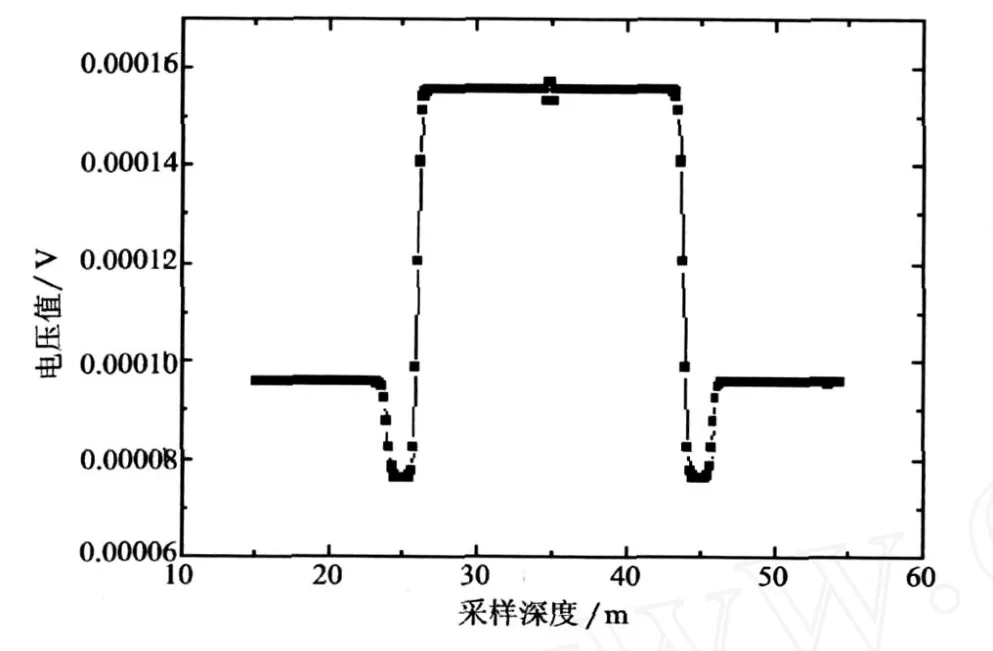
图5 串行计算采样点实部电压散点图
[1] 万 水,陈建平.有限元程序生成系统及其在工程中的应用[J].船舶力学,2004,8(3)
[2] 赵增辉,王育平,陈 波,等.基于FEPG的压电复合结构动态问题求解[J].山东科技大学学报(自然科学版) 2008,27(5)
[3] 胡 启,仵 杰.感应测井理论[M].西安:陕西人民教育出版社,1990
[4] 晁立东,仵 杰,王仲奕.工程电磁场基础[M].西安:西北大学出版社,2002
[5] 北京飞箭软件有限公司.FEPG.GID使用手册.2003(资料)
[6] 北京飞箭软件有限公司.FEPG用户手册.2003(资料)
[7] 黄 成.基于FEPG的电磁场计算若干问题的研究[D].北京:华北电力大学,2004
P631.8+3
B
1004-9134(2010)02-0079-03
张妙瑜,女,1980年生,硕士在读,讲师,现在西安石油大学电子工程学院主要从事信息探测与处理技术方面研究。邮编:710065
2009-11-21 编辑:高红霞)
·方法研究·
