随机冲击、货币政策与经济周期波动
2010-01-30张成思
张成思
一、引言
自1978年改革开放至今的30多年发展进程中,中国从“双轨过渡”的渐进改革模式开始,稳步推进经济体制和经济运行机制转轨,逐步转变经济发展模式,并且逐渐完善和优化货币政策的调控机制。与此同时,我国经济周期波动性特征在近年来呈现出“高位-平缓”的新轨迹。特别是自20世纪90年代中期以来,真实GDP增长率的波动幅度与此前相比明显趋缓。为了说明问题,图1描绘了1979年第1季度至2008年第4季度中国真实GDP同比增长率的季度数据以及对应期间年度数据的动态路径。①数据的来源在后文的数据描述与分析部分进行说明。从图1可以清楚地看到,真实GDP增长率在20世纪80年代和90年代波动比较剧烈,尤其是在80年代中期和90 年代初,经济出现大幅度波动,波峰超过16 %(1985 年),而波谷又跌至接近于0(1990 年)。进入新世纪之后,经济周期基本没有出现这种大幅波动的情况,虽然在20 08 年受到全球金融危机冲击,经济增长出现短暂下滑,但整体来看,波动幅度仍然比较温和。

图1 中国真实GDP增长率:1979年第1季度至2008年第4季度
中国经济周期波动性特征的这些动态变化一直是学界关注的焦点,经济学者对我国经济周期波动的原因也进行了长期的探索和研究,不同时期研究的重点有着紧密的内在联系。在20世纪80-90年代,以卢建[1]、陈越[2]、中国宏观经济运行状况研究课题组[3]和樊明太[4]为代表的经济周期波动性研究,集中探索了改革开放初期中国经济周期出现大波动的发生机理与缓和波动的思路,分别发现需求和供给层面的冲击以及宏观调控机制不健全是20世纪90年代以前我国经济周期大幅波动的主要原因。
最近几年来,相关研究的重点转向我国经济周期波动出现缓和化的原因。一方面,刘树成指出,20世纪90年代之后我国经济发展的体制基础、供求格局等方面发生的深刻变化是经济周期波动趋缓的原因。[5]供求格局的变化实质上反映了不同阶段需求冲击与供给冲击产生作用的机制和效果的改变。也就是说,早期文献中所指出的改革初期频繁出现的供给与需求冲击的属性现在已经发生转变,因此,经济周期波动随之减缓。
另一方面,一些研究者强调宏观政策特别是货币政策的系统性改进对经济周期波动缓和化的作用。例如,刘霞辉从货币与宏观经济波动的关系的角度进行研究,指出货币政策对经济周期波动性特征发生转变有显著影响。[6]孙稳存则认为货币政策变量波动性的变化(而非货币政策自身的改进)是促成近年来我国经济周期波动出现缓和化的最主要原因。[7]虽然这一解释似乎与我国经济周期波动和货币政策波动存在同起同落的现象相一致,但是必须假设货币政策波动性是外生因素,否则,经济周期波动性也可能是货币政策波动性的动因。贾俊雪和郭庆旺更关注货币政策以及财政政策自身的改进对经济周期波动减缓的解释程度,并利用GARCH模型和时变参数模型的估计结果说明,货币政策和财政政策的不断改进是中国经济波动出现缓和化的主要原因。[8]
以上研究对理解中国经济周期波动性特征发生转变的动因具有重要意义,并且将动因分析的重点缩小到冲击因素与宏观政策因素方面。但是已有的研究也提出了两个需要进一步探索的重要问题:一是经济周期波动性特征发生转变的确切时间,二是冲击因素与政策因素(特别是系统性货币政策)分别对经济周期波动转缓的量化解释程度。针对第一个问题,目前学界对经济周期波动性特征发生转变的准确时间还不明确,甚至存在一定的争议。这个问题的关键在于,经济周期波动特征的结构性转变时点属于内生变量,因此,需要运用未知断点检验来进行识别。针对第二个问题,即冲击因素变化与系统性货币政策的改进分别对经济周期波动缓和化的量化解释程度,目前还缺少严谨的对比研究,已有文献也尚未达成共识。而深入研究二者对经济周期波动缓和化的具体贡献程度,对决策层细化宏观政策调控方向、充分应对随机干扰因素对经济发展的影响具有重要的现实意义。
有鉴于此,本文首先运用存在干扰系数情况下的未知断点检验方法来判定我国经济周期波动特征出现结构性转变的准确时点,进而依据中国经济发展与货币政策的互动特征构建结构向量自回归模型(SVAR),并运用新近发展起来的反事实对比实验方法分析经济周期波动出现大缓和的动因。在具体分析过程中,我们还充分注意到我国财政和汇率等其他层面的政策变量对实体经济都有可能产生影响的现实,因此,分别进行了多角度的稳健性检验,并探讨了实证结果对经济发展、政策调控以及经济体制改革的深层含义。在文章的结构安排方面,第二部分对使用的数据进行描述与分析;第三部分介绍含有干扰参数(nuisance parameter)的未知断点检验过程与结果;第四部分构建SVAR模型,并以SVAR模型为基础进行反事实对比实验分析;第五部分总结全文并归纳研究结果的相关启示。
二、数据描述与分析
在实证研究中,数据使用的透明性与一致性对结果的准确性和可靠性至关重要,因此,有必要对使用的数据进行明确的说明。本文研究的样本区间为1979年第1季度至2008年第4季度,实证分析中涉及的主要变量包括真实GDP、CPI通胀率、货币供应量(M1和M2)、国内信贷总额、财政赤字与名义GDP的比率以及真实有效汇率。其中,货币供应量、国内信贷总额以及真实有效汇率的季度数据来源于国际金融统计;CPI通胀率的原始数据(月度)来源于国家统计局(经济景气月报);财政赤字(月度)与名义GDP(季度)的原始数据来源于WIND资讯。①财政赤字月度数据只有1990年1月之后的,1990年之前的季度数据依据CEIC公布的年度数据按季度平均获得。对于月度频率的数据,我们使用各季的最后一个月观测值作为对应的季度数据,以避免数据在频率转换过程中引入序列相关性。
针对GDP数据,还需要说明以下几点。首先,由于我国目前只公布1992年以来的名义GDP季度数据和对应期间的不变价格增长率,因此,我们使用阿贝森和古拉斯卡(Abeysinghe and Gulasekaran)的方法,将国家统计局公布的1978—1992年真实GDP年度数据换算为季度数据,进而计算出对应的同比增长率,从而获得本文研究样本区间所需要的真实GDP增长率的季度数据。[9]其次,为了进一步说明真实GDP增长率波动性的动态变化情况,表1按每隔10年的时间段报告了真实GDP增长率季度以及年度数据的标准差和均值统计量。从表1归纳的信息来看,1979年至2008年期间,真实GDP增长率的均值变化不大(9.5%~10%),但是其波动性在进入21世纪以后大幅减弱,降幅超过55%,这充分说明了我国宏观经济波动出现大缓和的事实。
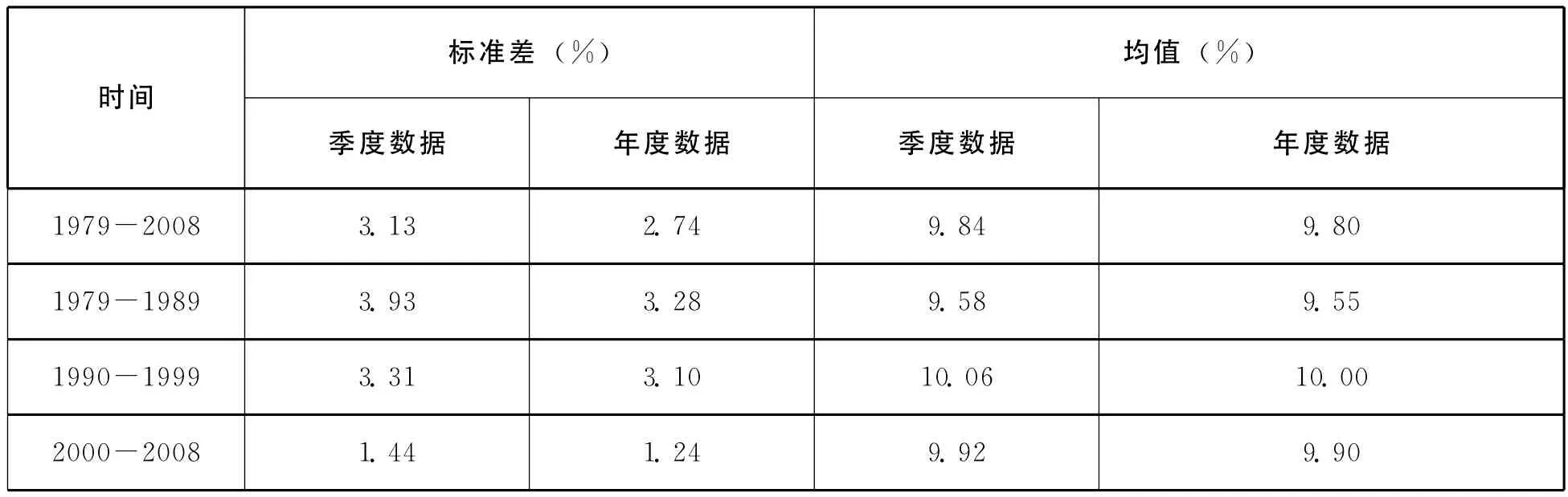
表1 中国真实GDP增长率的均值与波动性
另外,在实证分析中,真实GDP、货币供应量、国内信贷和真实有效汇率统一为同比增长率形式(因此,不再进行季节性调整),并分别以RGDPGR、M2GR(M1GR)、CREDITGR和DEER来表示;M1GR、M2GR以及CREDITGR用以刻画货币政策,财政赤字与名义GDP的比率用来代表财政政策变量,记做FISCAL;CPI通胀率简记为CPI。为确保计量估计与统计推断真实可靠,我们在实践中还对这些变量进行了传统的平稳性检验(如ADF和PP单位根检验),结果表明,各变量平稳性的假设比较合理。
三、经济周期波动性特征转变:内生断点识别
从前文分析中我们看到,真实GDP增长率的波动性在最近十几年来大幅减缓,而要识别这种缓和化转变的具体时点,首先需要设立动态模型来刻画真实GDP增长率的动态演进路径,进而对该动态模型进行结构性变化检验。为了与学界的标准研究(如Stock and Watson的研究)[10]相一致且不失一般性,我们首先使用p阶自回归模型AR(p)来捕捉真实GDP增长率的动态路径,即
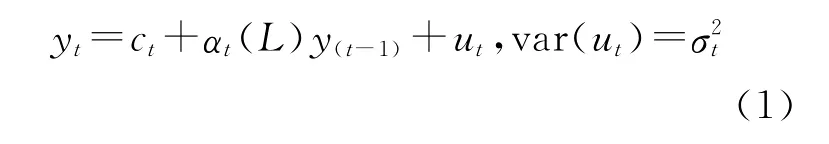
其中,ct表示截距项,at(L)表示滞后算子多项式[最优滞后阶数p由信息准则(如AIC)确定],ut表示无序列相关性的随机干扰项。注意,模型中系数和扰动项方差的下标都加了时间t,用以强调系数和方差可能存在结构性变化。接下来,为了判断真实GDP增长率的波动性(即方差或标准差)是否发生转变,我们需要根据模型(1)写出y的方差表达式,从而判断出哪些因素的改变可能导致方差发生变化,进而对相关因素进行断点检验。
依据标准的时序分析理论,y的方差可以写成:
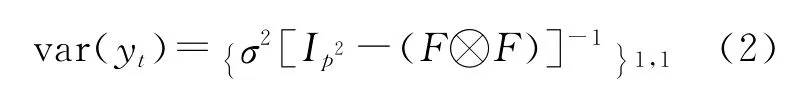
其中,等式(2)最右侧的下标(1,1)表示中括号内矩阵的首个元素,F表示由模型(1)中的自回归系数a1(i=1,2,…,p)以及0和1组成的p×p阶矩阵,σ2表示模型(1)中扰动项的方差。由等式(2)可以看出,真实GDP增长率的方差发生变化,可能由三种情况导致,一是自回归系数发生改变,二是随机冲击项的方差发生变化,三是两种变化同时发生,但与截距项无关。所以,内生断点检验需要分别检验自回归系数(即条件均值)和随机冲击项的方差(即条件方差)是否发生结构性变化。而无论哪种检验,都涉及干扰参数问题(即断点作为一个待估计参数只出现在备选假设中)。由于干扰参数的存在,对应的检验统计量不再服从标准的统计分布,统计量对应的伴随概率也就不能由标准条件下的统计分布函数计算。为此,我们运用安德鲁斯和普罗伯格(Andrews and Ploberger)提出的存在干扰系数情况下的未知断点结构性变化检验方法[11],并利用汉森(Hansen)提出的非标准分布条件下的渐近伴随概率分布函数[12],来计算干扰参数检验统计量对应的p-值,从而判定条件均值和条件方差发生结构性转变的具体时点。
另外,由于AR系数与扰动项方差的断点时刻可能不同,因此,我们假定AR系数的结构断点发生在k时刻,而扰动项方差的断点发生在n时刻,则有:

我们以AR系数结构性变化检验为例来说明未知断点检验的过程,var(ut)的检验与此类似。根据安德鲁斯和普罗伯格的理论,假定p×1阶的向量γ表示模型(1)中所有AR系数,在t<k时有γ=γ1,而在t≥k时有γ=γ2(γ1≠γ2),并且满足条件p≤k≤T-p,其中,T表示有效样本大小。另外,假设未知结构断点参数的搜索域为τ,首先计算在该域内所有可能的断点k=Tτi对应的一系列Wald检验统计量WT(τi),该统计量检验的原假设是在结构断点为k时模型中参数不发生结构性变化。不难看出,对于原假设来说,这个未知断点参数k并不出现,而只是出现在备选假设条件下,所以,这里的检验涉及干扰参数问题。在获得所有WT(τi)之后,进一步计算其中最大的Wald统计量,即

Sup W统计量对应的时刻即为发生结构性变化的转变时点。安德鲁斯和普罗伯格指出,依据Sup W统计量可以进一步计算具有统计最优特性的指数-Wald(Exp W)和均值-Wald(AveW)统计量,我们在实践中也根据这两个统计量各自的定义进行了计算。在实际计算过程中,考虑到可能存在的异方差性,我们使用无约束条件下模型的异方差修正矩阵结合汉森的非标准分布函数来计算对应的p-值;断点检验的搜索域设定为标准的有效样本中间70%,以保证左右端样本各有0.15×T个观测值。
根据以上介绍的方法,表2报告了未知断点检验的结果。从AR系数对应的结果来看,虽然在1%的显著性水平下Sup W和Exp W统计量具有显著性(AveW不显著),但是观察断点时间可以看到,2004年第1季度指向了搜索域的极端点,说明这一断点并不准确(由极端值造成)。而条件方差的检验结果显示,所有检验统计量均具有显著性(Sup W在10%水平下显著),对应的断点时刻为1995年第4季度,这一转折点与现实中我国真实GDP增长率的波动性动态路径变化情况基本吻合。另外,我们在实践中还以1995年第4季度作为断点进行邹氏(Chow)断点检验,检验统计量对应的p值小于5%,从而进一步说明结构性变化断点识别的稳健性。综合以上分析,结构性变化检验的结果说明,真实GDP增长率的波动性特征确实发生了显著的结构性转变,而发生转变的分水岭是1995年第4季度。这一断点的识别为下面进一步分割样本研究我国经济周期波动出现缓和化的动因提供了可靠的依据。

表2 真实GDP增长率AR模型未知断点检验:1979年第1季度至2008年第4季度
四、SVAR模型与反事实对比实验分析
(一)SVAR模型的设立
近年来,随着宏观经济理论的不断发展与完善,投资存储—总供给—货币政策(IS-ASMP)的分析框架已经逐渐发展成为研究货币政策与经济产出动态关系的标准范式。在这样的系统内,IS等式、通胀动态等式和货币政策反应方程是核心要素。如果使用yt表示真实经济产出增长率,πt表示通胀率、it表示名义利率,我们可以将程式化的系统表示为:
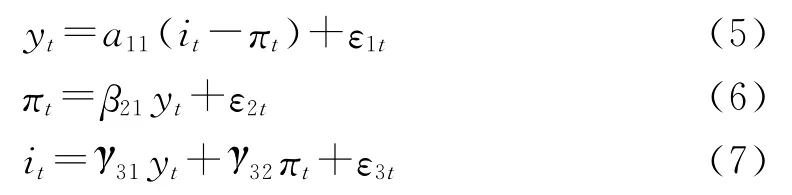
等式(5)描述的是IS等式(即欧拉等式),等式(6)刻画的是通胀动态等式(即菲利普斯曲线),等式(7)是货币政策反应方程。等式中的扰动项ε依次分别表示需求冲击、供给冲击和货币政策冲击。
这一系统所刻画的货币政策与经济发展互动的理论逻辑非常清楚。具体来说,真实利率(即名义利率剔除通胀率)下降会刺激投资,从而带动真实经济产出增长加快,而经济产出增长率上升会带来通胀上升压力,此时货币当局就会针对通胀率和经济增长率的变化而调节政策工具,而利率发生变化以后又会再次通过IS等式作用于真实经济产出。这样,货币政策与真实经济产出就形成了明确的动态传导机制。
虽然这一动态系统在宏观经济分析中得到了广泛的认同,但是在IS-AS-MP的大框架下,不同的文献中具体模型设立的形式存在一定的差别。这一方面是因为不同研究的侧重点不同,另一方面是由于所分析国家的经济运行机制彼此之间有差别。因此,我们在构建多维动态模型的过程中,既要充分考虑到分析问题的可行性,又要兼顾中国经济运行机制和货币政策调节机制的特点,不能简单地以“中国经济发展具有特殊性”为由完全脱离相关经济理论的基本框架。为此,我们在分析中国经济发展与货币政策互动关系的过程中,特别注意到以下几点重要的区别。
首先是货币政策工具的差别。尽管近年来我国货币政策传导机制中越来越重视价格型工具的作用,但目前利率市场化程度与西方发达国家的水平仍然存在较大差距,中国人民银行也明确提出我国货币政策主要以总量控制为中介目标。因此,我们可以利用货币需求函数(即LM关系式,其中M、P和Y分别表示货币总量、价格总水平与真实GDP总水平,f(.)表示函数关系)

经过对数线性化、线性差分并与等式(5)~(7)相结合,将货币供给增长率作为货币政策工具引入动态系统内,整理之后可以获得刻画我国货币政策与经济发展动态关系的模型系统,即
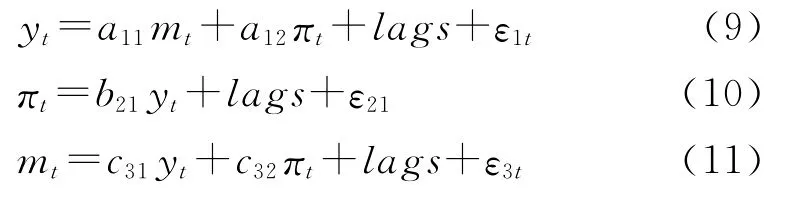
与之前的系统不同,这里真实GDP增长率与货币供给增长率(以及通胀率)相关;货币供给增长率作为政策工具对真实经济产出增长率和通胀率的变化进行调整;各个等式中的“lags”表示各变量的滞后项,用以捕捉现实中客观存在的动态效应(实证分析中由SIC准则确定)。
其次,改革开放以来,中国经济发展过程中运用了多种调控工具作为宏观政策的指标,为了使结果具有稳健性,本文在实证分析过程中不仅重点研究了货币政策对经济周期波动性特征转变的贡献度(货币供给增长率和信贷增长率代表货币政策),而且考察了财政政策和汇率政策可能带来的影响(其中,以财政赤字与名义GDP的比率代表财政政策,以真实有效汇率代表汇率政策),以期使分析结果更具全面性。
综合以上分析,我们可以将本文设立的SVAR模型的基本形式简写成:

其中,εt表示由彼此正交的供给冲击、需求冲击和货币政策冲击所组成的随机冲击向量;结构冲击项的方差-协方差矩阵Ω为对角矩阵。Yt包含真实GDP增长率、通胀率以及政策变量。例如,当使用M2增长率表示货币政策指标时,Yt=[RGDPGR,CPI,M2GR]′,当考察其他政策变量对经济波动的影响时,SVAR中Yt的定义依此类推。注意,在运用上面提到的政策指标变量分别估计SVAR模型的各种稳健性分析中,我们还检验了当货币政策变量与财政政策变量同时进入模型系统内,以及货币政策与财政政策分别与汇率政策组合时的结果。
(二)反事实对比实验
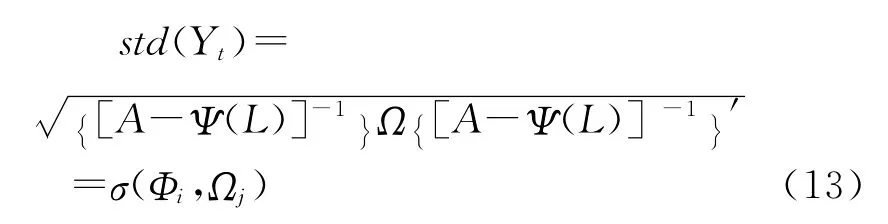
反事实对比实验分析是依据本文第三部分获得的真实经济波动性发生变化的转折点(1995年第4季度),对SVAR模型进行分割样本估计,然后将不同样本区间估计的参数结果进行反事实互配,从而计算货币政策的系统性改进(即SVAR模型系数变化)与冲击因素的属性变化(即冲击项方差变化)分别对经济波动缓和化的解释程度。具体来说,依据模型(12)的设立形式,如果我们把系数矩阵A和Ψ(L)统一记做φ,则可以解出真实GDP增长率在整个模型系统下的标准差(std(Yt)),即下面等式中的矩阵对角线上第一个元素:其中,下标i、j用来区分样本区间。这样,只要在一定识别条件下估计出SVAR模型在指定样本区间的系数矩阵Φ和扰动项的方差-协方差矩阵Ω,就可以通过等式(13)计算对应的真实GDP增长率的波动性水平。例如,σ(,)给出的是依据SVAR模型在1979—1995年区间的估计结果计算出的真实GDP增长率的标准差;σ(,)表示利用1995年以后的样本信息估计SVAR模型后计算出的标准差;而σ(,)则表示如果系数矩阵利用第一个样本区间的结果而方差-协方差矩阵使用第二个样本区间的结果,那么,真实GDP增长率的标准差是多少。其他情况依此类推。
通过这样的对比实验,我们可以考察货币政策发生的系统性改变(SVAR系数矩阵变化)与随机冲击因素的性质发生变化分别对真实GDP增长率的波动性解释程度有多大。注意,为充分考虑到政策工具与通胀率对经济产出的滞后作用,SVAR模型的识别依据短期约束条件,在估计出SVAR模型的相关参数之后,我们根据等式(13)分别计算了不同情况下真实GDP增长率的波动性水平,结果报告在表3中。

表3 SVAR模型反事实对比实验估计结果(真实GDP增长率波动性)
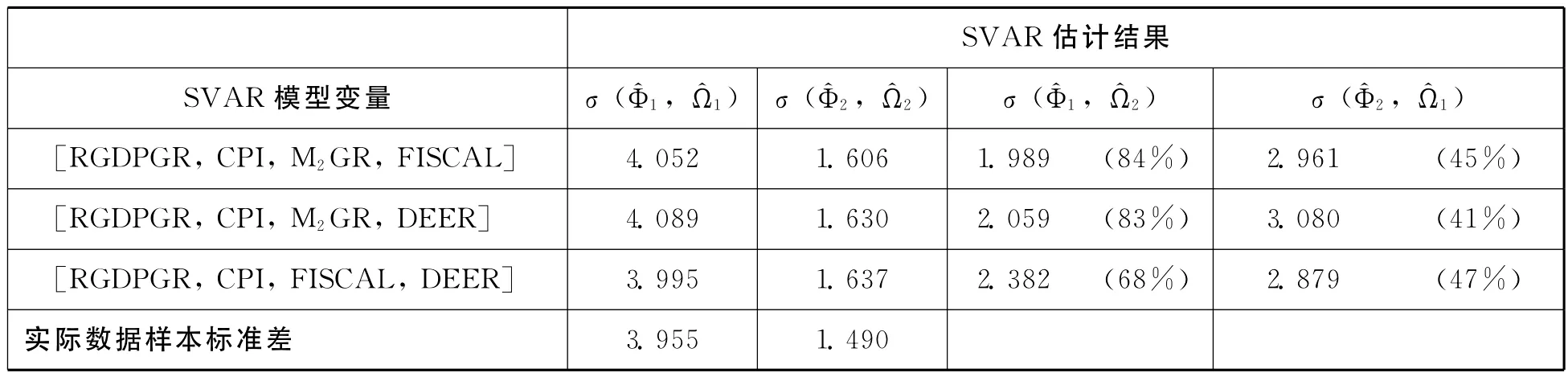
续前表
首先,利用SVAR模型估计的参数所计算出的断点前后真实GDP增长率的波动性水平分别是4.012和1.586,这两个估计值与直接利用实际样本计算的真实GDP增长率标准差(即最后1行报告的3.955和1.490)非常接近。这一方面说明所设立的SVAR模型系统能够较好地刻画我国实体经济、通货膨胀与货币政策之间的现实动态关系,另一方面也再次验证了1995年之后我国真实GDP增长率的波动性出现大幅减缓的事实。从减弱幅度来看,无论是实际数据的分样本估计还是SVAR模型的估计结果,均超过60%。这一水平要比发达国家的降幅(40%左右)[13]更高,说明中国经济波动缓和化程度要远远超过发达国家的情况,这也更突出了研究中国经济波动缓和化问题的重要性和必要性。
其次,表3中最后两大列报告的分别是依据SVAR系数矩阵与扰动项方差-协方差矩阵在断点前后进行反事实搭配所计算的真实GDP增长率波动性水平。从具体数值来看,如果系数矩阵保持不变而令结构冲击项的方差-协方差矩阵改变为第二个样本对应的结果(即σ(^Φ1,^Ω2)),真实GDP增长率的标准差由4.012减小为2.045;如果系数矩阵改变为第二个样本对应的结果,而结构冲击项的方差-协方差矩阵保持不变(即σ(^Φ2,^Ω1)),真实GDP增长率的波动水平则降低到2.974。根据这些结果,还可以进一步计算在这两种反事实对比实验中,系数变化与冲击项方差-协方差矩阵变化分别对真实GDP增长率波动水平降低的贡献百分比,结果显示在对应情形下的小括号内。
我们看到,如果不考虑SVAR模型中系数的变化,结构冲击项的波动性变化对宏观经济波动缓和化的解释程度为81%(即(4.012-2.045)/(4.012-1.586));而反过来,如果不考虑结构冲击项波动性的变化,SVAR模型中系数的改变对经济波动缓和化的贡献为43%;当二者共同变化时,就促成了我国真实GDP增长率在1995年之后降低至不到此前的40%。如果按照冲击项与系数各自变化分别对经济波动缓和化的贡献比例(81%÷43%=1.88)来计算,SVAR系数变化对经济波动缓和化的贡献度为35%(1/2.88),而冲击项波动性的变化解释度为65%。如果以M1增长率或国内信贷增长率作为货币政策指标进行反事实对比实验(表3中第2行和第3行),估计结果与M2增长率作为货币政策变量的结果基本相同。
接下来考察各种稳健性分析的结果。其中,表3中第4行考虑财政赤字与名义GDP的比率作为财政政策指标的对应结果,第5行对应的是同时将M2增长率与财政政策指标加入SVAR模型的结果,接下来的两行分别报告了以汇率政策与货币政策以及汇率政策与财政政策指标进行组合获得的结果。从这些稳健性分析的反事实对比实验结果来看,结构冲击项波动性改变对经济波动缓和化的解释程度都要高于SVAR模型系数变化的贡献程度,二者解释程度的比例介于1.45~2.02之间(2.02与1.45这两个数值分别发生在最后两个稳健性实验中)。也就是说,SVAR系数的变化对经济波动缓和化的解释程度介于33%~41%之间,而结构冲击项波动性变化的解释度为59%~67%。
值得注意的是,虽然财政政策对经济波动缓和化的解释程度与货币政策的解释度基本相同,但是当二者同时加入SVAR模型中时并没有给出双倍的解释效果。这反映出一个深层次的问题,即我国财政政策与货币政策的职能界限比较模糊,至少在调节经济波动的效果上,财政政策与货币政策表现出“你中有我、我中有你”的状态。这种结果可能与一段时期以来我国银行在财政开支过程中扮演的重要角色相关(例如,各类银行购买国债并通过财政开支向社会投放货币),这也暗示出未来财政与货币政策需要以史为鉴进行调整和改进的一个重要方向。
总起来看,表3中的多种稳健性分析所给出的结果基本一致,无论是以货币指标、信贷指标、财政指标、货币与财政指标的结合,还是将汇率动态变化也考虑到模型系统内,依据SVAR模型计算的真实GDP增长率的波动性在1995年以后都大幅下降。从驱动因素的量化解释来看,我国系统性货币政策的发展与完善(反映在SVAR模型的系数变化上)对1995年以后经济波动转缓的解释程度在30%~40%左右,而结构冲击项波动性的变化的解释程度更高一些,一般介于60%~70%之间。
五、结论与启示
随着我国经济市场化改革的不断深入,货币政策在调控经济周期波动中的地位日益增强。特别是进入21世纪以来,我国的货币政策调控机制从以往的直接管制发展为间接调控,其他各种宏观稳定政策也得到了卓有成效的积极改进。与此同时,中国宏观经济波动特征也出现了令人瞩目的平缓化转变。那么,经济波动缓和化的具体转变时点是什么时间?货币政策的发展与改进是否与经济波动缓和化的发展存在着紧密联系?政策改进对经济波动转缓的量化解释程度是多大?本文的研究主要回答了以上问题。
我们运用存在干扰参数情况下的内生断点检验方法,识别出1995年第4季度是改革开放30年来我国经济周期由大波动转变为大缓和的分水岭。根据这一转折点,本文进而依据我国货币政策与经济发展的动态联系特征,构建了相对简约的SVAR模型,并且运用反事实对比实验方法计算出货币政策改进与随机冲击因素波动性变化分别对经济波动转缓的解释程度。经验分析结果显示,我国经济周期波动出现大缓和的首要原因是宏观经济运行过程中的各种冲击因素波动性发生了变化,其次是货币政策调控机制的系统性改进。这一结果在考虑其他相关政策的影响时仍然具有稳健性。
这一发现不仅对总结改革开放30年来的实践经验具有重要启示,而且对新形势下保持总体经济平稳发展、提升货币政策效果提出了值得深入思考的问题和改进的方向。
首先,尽管经济运行环境的改善(冲击因素波动性减弱)确实能够解释我国经济周期波动缓和化的主要动因,但是冲击因素属性的变化是一种被动式的推动因素。从长期来看,经济运行的稳定性不能依赖于这种随机要素的变化。相反,货币政策的系统性改进应该成为缓和经济周期波动的主动因素。需要说明的是,西方发达国家经过20多年的政策改进,货币政策对宏观经济稳定的贡献只有10%~20%。因此,虽然我国货币政策的发展与完善对经济波动缓和化的解释程度低于冲击因素的解释度,但是要客观地认识到,在短短13年时间内(1996—2008年)货币政策的改进带来30%~40%的贡献已经是相当大的成绩。从这个角度看,即使随机冲击因素的波动性没有发生改变,我国经济周期波动性在1995年以后仍然会在宏观稳定政策的带动下出现相当程度的缓和。
其次,本文的经验结果也表明当前货币政策仍然具有较大的改进与提升空间。从政策发展与改革的具体方向来看,有三个方面的内容值得关注。第一,在推进政策改革的进程中,需要注意区分不同经济发展阶段的主要矛盾。在20世纪80—90年代,缓解扩张冲动与投资饥渴是政策的主要改进方向。而当前的主要矛盾已经不再是投资扩张问题,更重要的是需求(特别是有效需求)不足问题。针对这一问题的货币政策调整对进一步缓和宏观经济波动具有重要意义。第二,随着我国经济运行的市场机制进一步完善,市场预期在经济发展的微观和宏观层面都具有不可忽视的影响。因此,提升货币政策的前瞻性是最重要的任务之一。而要提高政策制定的前瞻性,科学的经济预测系统的建立与完善非常关键。第三,进一步明确和区分财政政策与货币政策的职能,有步骤地推进货币政策的独立性。在这个过程中,强化货币政策对短期经济波动的干预效果,同时提高财政政策对长期经济发展目标的职能,并且保持汇率政策的稳定性,这些是进一步完善当前宏观政策调节机制值得考虑的问题。
最后,笔者认为,我国财政政策与货币政策的职能分配还有待进一步加强。例如,我国曾实行的“拨改贷”将国家对国有企业的拨款改为统一由银行贷款来解决,虽然这一举措为解决一定时期的特殊问题发挥过积极作用,但从一定程度上使中央银行通过银行系统调控贷款的标准和自主性缺失,也造成货币政策与财政政策的职能混淆不清,致使财政资金和信贷资金在使用过程中界限模糊、互相挤占,从而影响了财政政策与货币政策的协调和运行。要更好地解决这些矛盾,大力推进利率市场化改革、优化金融资源配置是未来发展的必要策略。这样,随着宏观调控机制的不断改进和完善,即使在全球金融局势动荡的冲击下,我国经济增长波动平缓化的良好局面也仍然能够继续保持下去。
[1]卢建:《我国经济周期的特点、原因及发生机制分析》,载《经济研究》,1987(4)。
[2]陈越:《中国经济周期问题研究》,载《管理世界》,1988(1)。
[3]中国宏观经济运行状况研究课题组:《中国经济波动的原因探析》,载《管理世界》,1992(4)。
[4]樊明太:《改革前后中国经济波动机制的比较分析》,载《管理世界》,1995(5)。
[5]刘树成:《新一轮经济周期的背景特点》,载《经济研究》,2004(3)。
[6]刘霞辉:《为什么中国经济不是过冷就是过热》,载《经济研究》,2004(11)。
[7]孙稳存:《货币政策与中国经济波动缓和化》,载《金融研究》,2007(7)。
[8]贾俊雪、郭庆旺:《中国经济周期波动特征变化与宏观经济稳定政策》,载《经济理论与经济管理》,2008(7)。
[9]Abeysinghe,Tilak and Gulasekaran Rajaguru.“Quarterly Real GDP Estimates for China and ASEAN4 with a Forecast Evaluation”.Journal of Forecasting,2004(23):431-447.
[10][13]Stock,James H.and Watson,Mark W.“Understanding Changes in International Business Cycle Dynamics”.Journal of the European Economic Association,2005(3):968-1006.
[11]Andrews,Donald W.K.and Ploberger Werner.“Optimal Tests When a Nuisance Parameter is Present only under the Alternative”.Econometrica,1994(62):1383-1414.
[12]Hansen,Bruce.“Approximate Asymptotic P Values for Structural Change Tests”.Journal of Business and Economic Statistics,1997(15):60-80.
