用边界点法分析任意形状板的自振频率

郑 炎， 肖永建， 许震宇

(西藏职业技术学院 建筑系， 西藏 拉萨 850030)

在很多工程问题中，常常要求求解广义代数特征值问题。而目前的有限单元法(FEM)、有限差分法(FDM)以及边界单元法(BEM)等数值方法在处理复杂几何形状的工程的本征值问题时，网格很难划分，并且划分网格很花费时间。近年来，无网格法越来越受到学者们的重视，其最初的思想可以追溯到用光滑粒子法(SPH)模拟天体物理学现象[1]，许多学者致力于用无网格方法求解偏微分方程(PDEs)的数值解。目前，无网格方法比较多，例如，无网格伽辽金法(EFGM)[2]，重构核点法(RKM)[3]，基本解方法(MFS)。

本文采用一种简单的由Chen和Tanaka[4，5]提出的无网格方法——边界点法(BKM)求解各种形状的板在各种边界条件下的固有频率。BKM是基于径向基函数(RBF)方法的一种，由于径向基函数方法不采用移动最小二乘法，用一维的距离变量来构造多元空间变量，不用划分网格。而BKM继承径向基函数的无网格特性，与维数和几何形状无关，是完全的无网格方法，不需积分，容易学习和编程。Chen和Hon[6]从数学上说明了BKM是谱收敛的，谱收敛就是说近似程度只和选择的物理解的光滑程度有关系。

Kang[7，8]和Chen[9]分别用无网格方法给出了夹支板和膜的自由振动的固有频率的数值解，然而对于计算复杂的高阶边界的板的自有振动的固有频率的数值解仍然有一定的难度。Kang[7]将劲度矩阵有2N×2N维降到N×N，这种方法能够加快计算速度，节约计算机内存空间，但降维的过程中有矩阵逆的操作，使矩阵的条件数变差，容易使劲度矩阵奇异，最终无法求解。另外，在处理多边形的角点的法向量时， Kang简单的将相邻两边的该点的法向量的矢量和代替该点的法向量，其法向量大于单位1。在计算夹支板和膜的固有频率时，是可行的，但是计算简支边和自由边时，误差很大，无法满足精度要求。本文的角点法向量也采用两边法向量的矢量和的方向，但是法向量的大小采用单位1，这样更合理，数值解也更精确。

1 板自由振动的控制方程

各向同性的薄板的自由振动方程为

w(r,t)=eiωtW(r)

(2)

其中，ω表示圆频率,W(r)为板的振型函数, 将方程(2)代入方程(1)有

(3)

(4)

其中k为板的频率参数。方程(3)的通解[10]为

W(r)=AjJ0(k|r-rj|)+BjI0(k|r-rj|)

(5)

其中，J0(r),I0(r)分别为第一类和第一类修正的贝塞尔函数，|r-rj|为边界点之间的距离(图1)，r为边界点的矢量,AJ,Bj为未知系数。

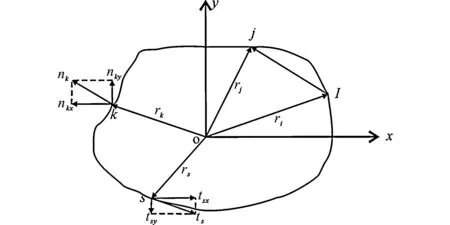
nk，τs分别表示点k，s处的法向量和切向量图1 任意形状的薄板的边界点的分布

如图1所示，在薄板的边界取N个点，任意一点的模态可以表示为

(6)

2 边界条件

薄板边界上的位移为

u=W(r)

(7)

薄板边界沿法向量方向的转角为

(8)

边界上的弯矩为

(9)

边界上的剪力为

(10)

相邻自由边的交点处的集中反力

(11)

式(11)中，u,θ,M,V分别表示边界的位移、转角、弯矩和剪力，R为相邻两自由边交点处的集中反力；v为泊松比；n,τ分别表示边界的法向量和切向量。对于各种边界条件的板，只需满足上述式(7)～(10)四个边界条件中的两个(有两相邻自由边还需方程(11)等于零就可以。需要强调的是，对于多边形的相邻两边的交点的法向量的法向为该点所属的两边该点的法向量的矢量和的方向，但大小为单位1。

将式(6)代入式(11)，并使表达式等于零，可得边界上任意一点的边界条件方程，即

i=1,2,…,N

(12)

i=1,2,…,N

(13)

i=1,2,…,N

(14)

i=1,2,…,N

(15)

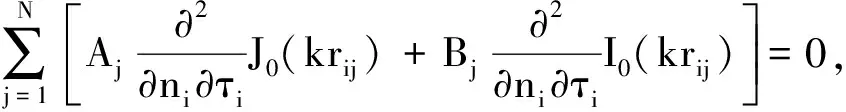
i=1,2,…,N

(16)

其中,rij=|ri-rj| 分别表示边界上第i个点处的法向量和切向量，如图1所示。

方程(12)～(16)可以用矩阵形式简单的表示为

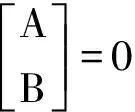
(17)

方程(17)左边的劲度矩阵的部分公式推导如下

(18)

(19)

方程(17)左边的劲度矩阵的其余公式的详细推导结果略。式(18), (19)中，nix，niy和τix,τiy分别表示单位法向量ni=nix+niy和单位切向量τi=τix+τiy在第i个边界点处的水平分量和竖直分量,θij为两点矢量ri-rj方向与x轴的夹角。

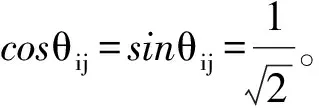
(20)

(21)

=0

(22)

可根据方程(22)求出各种边界的板的频率参数k。

3 算 例

3.1 方形板

三边简支一边自由的方形板(图2(a))被分成4N-4(每边N个)个点(图2(b))。部分点和

其相应的法线方向如图2(b)所示。方板的四个角的法线方向采用前述的处理方法处理。

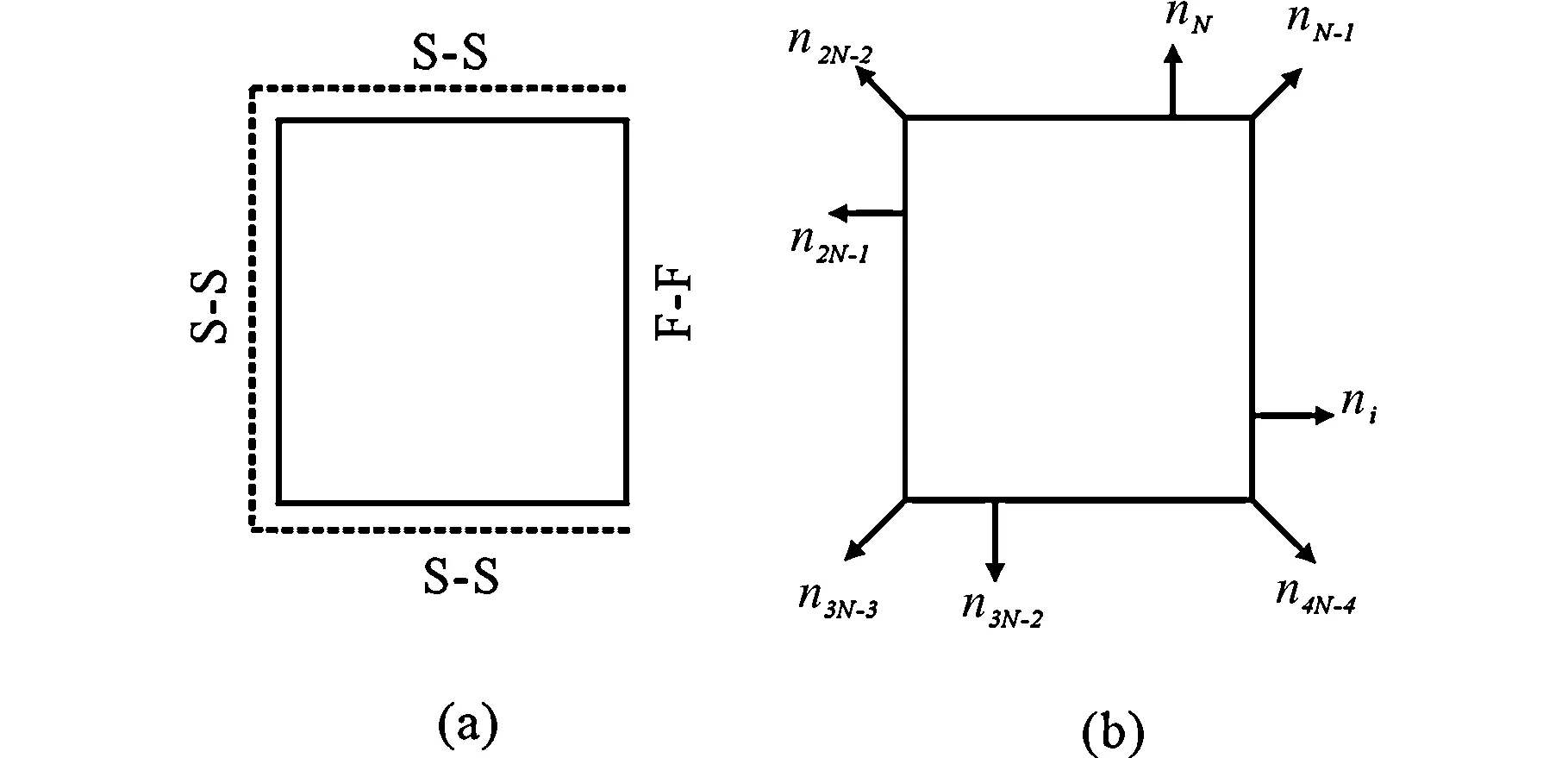
图2 (a)三边简支一边自由的方形板(其中S-S表示简支边，F-F表示自由边)(b)各边分成N等分时方形板的离散边界点和法线方向，ni表示第i节点的法线方向

从计算三边简支一边自由的方形板的结果可以看出，其包含有四边简支方形板的频率参数。因此，必须剔出这些不属于三边简支一边自由的方形板的频率参数。为简单起见，用SSSS(k)表示四边简支方板的的劲度矩阵，SSSF(k)、SF(k)分别表示三边简支一边自由方板的劲度矩阵和其特有频率的劲度矩阵。则三边简支一边自由方板的特有频率参数矩阵可以表示为

SK(k)=SSSF(k)[SSSS(k)]-1

(23)

在图3中，三边简支一边自由的方形板的频率参数能从det[SF(k)]=0的对数曲线中得到。波峰表示四边简支方板的频率参数，波谷表示三边简支一边自由的方板的频率参数，表1和表2分别给出了对应的频率参数值和与精确值的相对误差。

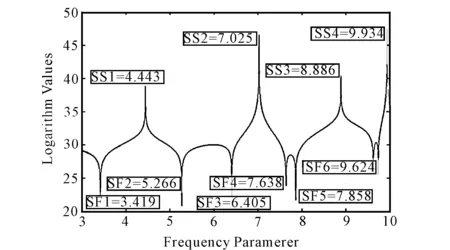
图3 N=6, ν=0.3时，矩形板的对数曲线det[SF(k)]，SF表示三边简支一边自由板频率参数，SS表示四边简支的频率参数

参数计算值20(N=6)相对误差24(N=7)相对误差28(N=8)相对误差精确解[11]SF14.44290%----4.4429SF27.02480%7.02480%7.02480%7.0248SF38.88580%8.88580%8.88580%8.8858SF49.9340-0.006%9.93460%9.93460%9.9346

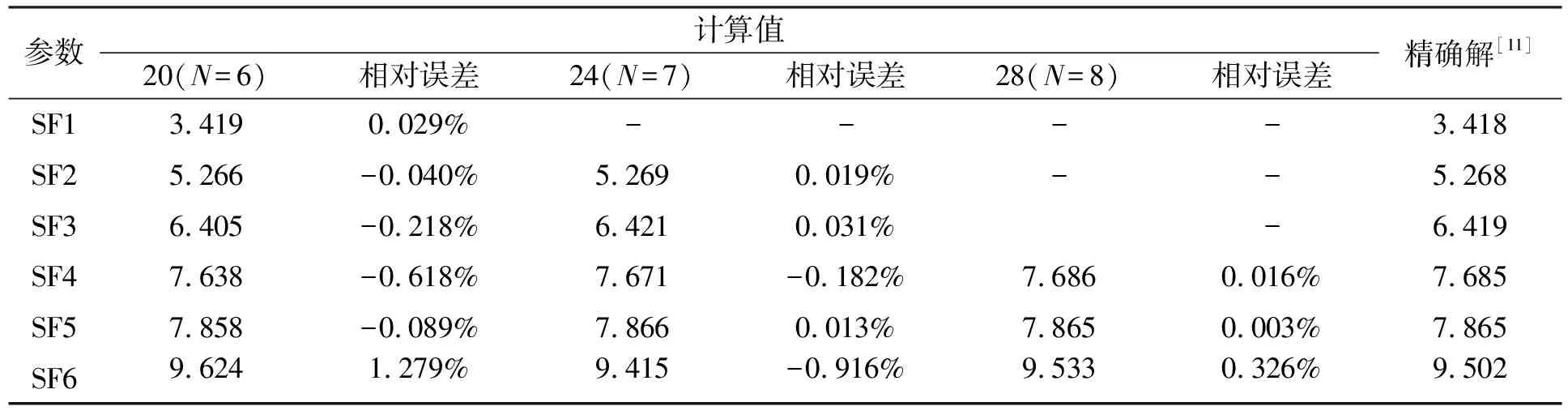
表2 三边简支一边自由方形板的频率参数值

从表1和表2中可知，20个边界点得到的频率参数值已经具有很高的精度，如果要得到更高阶参数，须取更多的边界点。采用同样的方法，可以计算任意边界条件下的方形板频率参数值。

3.2 任意形状的简支板

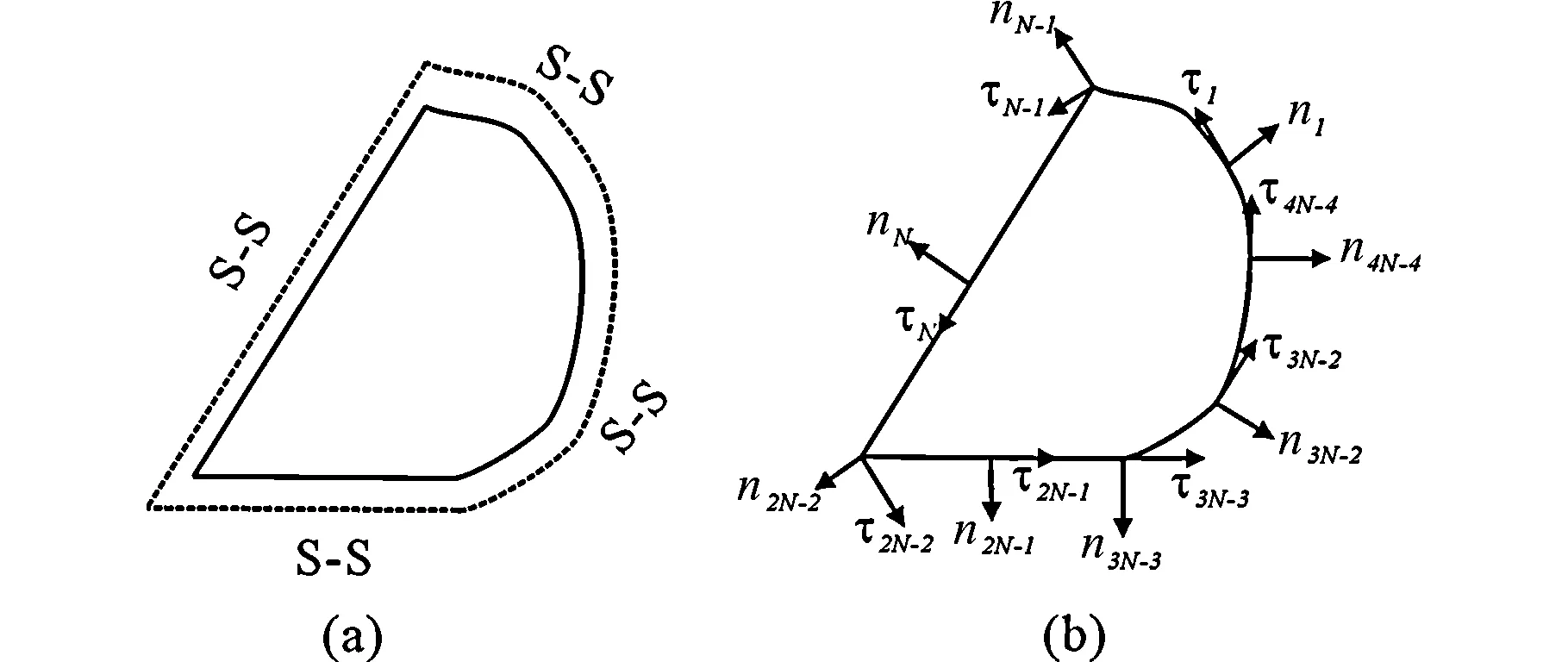
图4 (a) 任意形状简支板，S-S表示简支边，(b) 各边分成N等分时任意形状简支板的离散边界点的法线方向和切线方向，ni，τi表示第i节点的法线方向和切线方向

图4 (a)中，一个由半径为1 m的半圆和两个边长为1.5 m和2.5 m的边组成的域为任意形状板的形状，在其边界取4N-4点，每个点对应的法线方向和切线方向如图4 (b)所示。各边的交点处的法向量和切向量处理如前文所述。

在计算任意形状的简支板频率参数时，从计算结果的图形中可以看出，其迭代出的结果含有对应形状的膜的频率参数。因此，必须剔除这部分不属于任意形状简支板的频率参数。本文中，简支板的频率参数矩阵为(8N-8)×(8N-8)维，而对应形状的膜的频率参数矩阵为(4N-4)×(4N-4)维，剔除这些非本征频率参数必须降维。

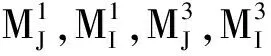
(24)

方程组(24)中的第一个方程可以写成

(25)

将方程(25)代入方程组(24)中第二个方程

(26)

膜的频率参数[7]方程为

(27)

则任意形状的简支板的特征频率参数方程为

(28)

方程(28)系数矩阵[A]有非零解，则其劲度矩阵的行列式为零

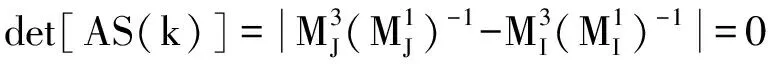
(29)

计算结果如图5和表3所示。图5为20个边界点的计算结果，其中AS,M表示任意形状简支板和膜的频率参数，6个波峰和7各波谷分别为det[AS(k)]的对数曲线对应的任意形状的膜和简支板的频率参数值。表3为20、30个边界点的计算结果与ANSYS软件计算结果的比较，由表中可以看出，计算精度很高。

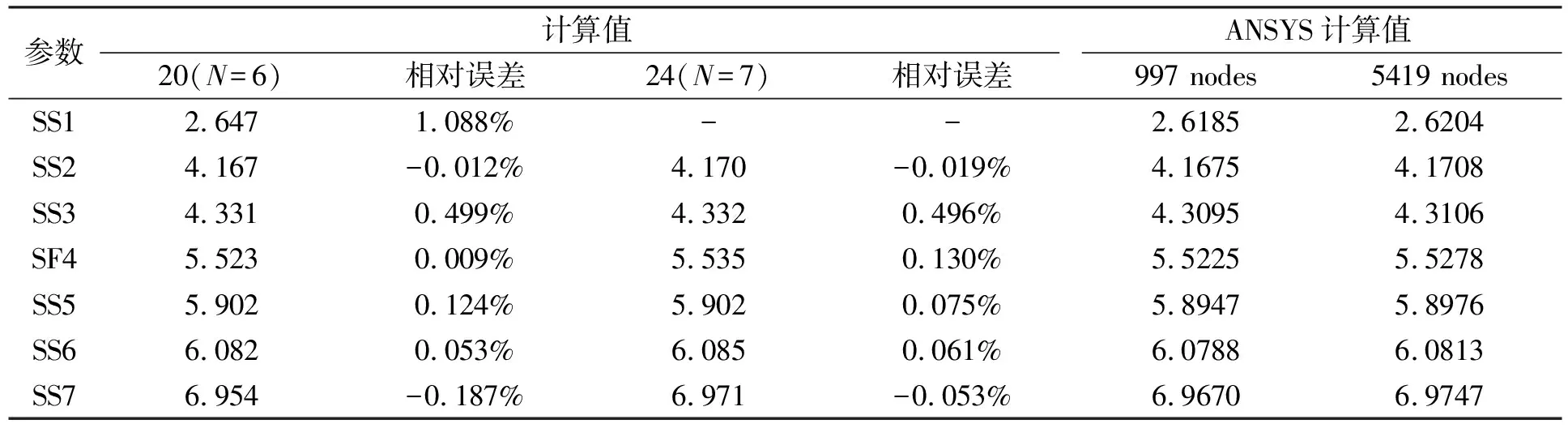
表3 BKM法计算任意形状简支板的特征值

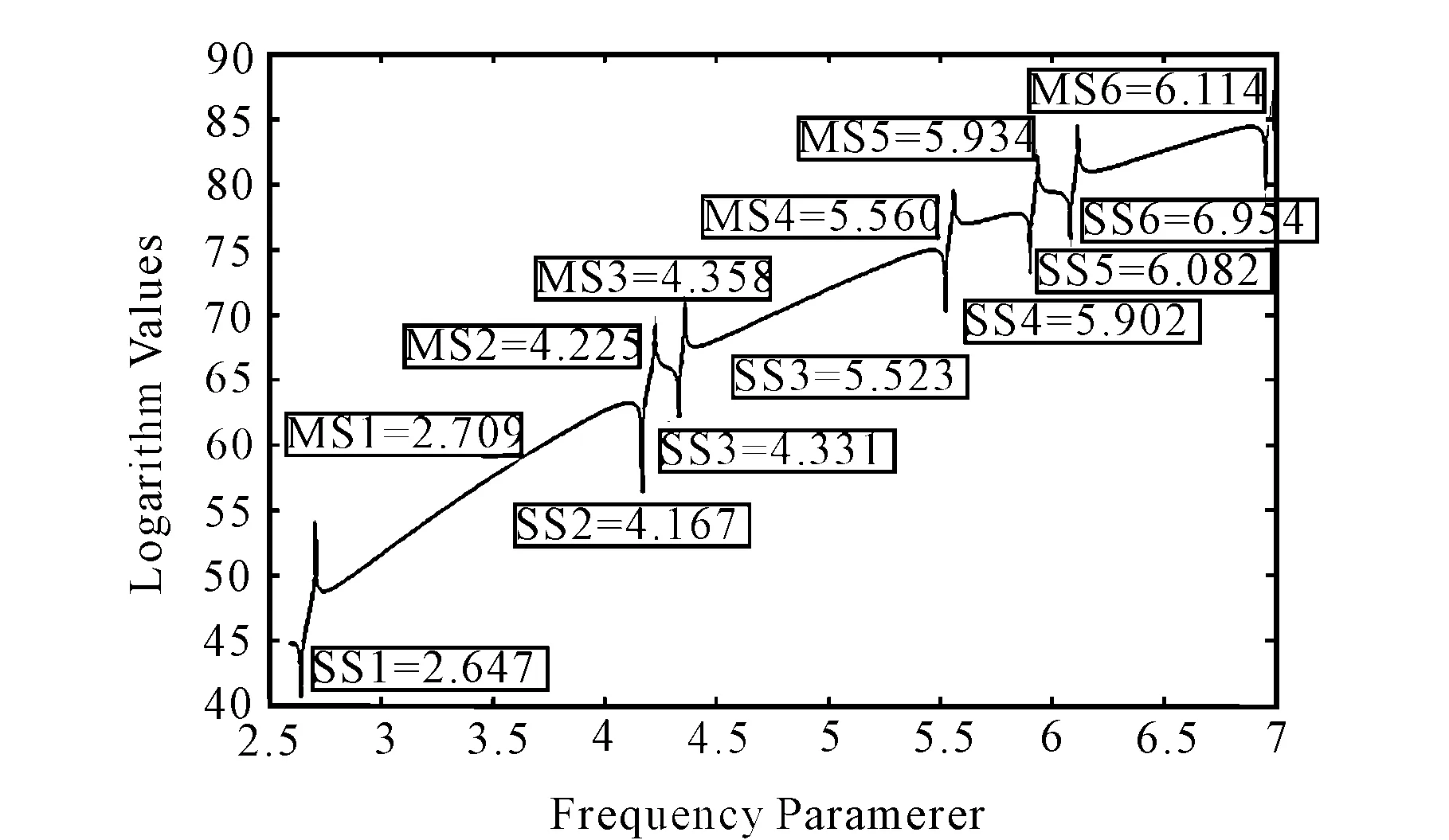
图5 当 N=6, ν=0.3时，矩形板的对数曲线det[FSSS(k)]，SS表示三边简支一边自由板频率参数，M表示三边简支一边自由膜的频率参数

4 结 语

BKM法可视为一种Trefftz法，其实验功能要求测试函数满足控制方程。“BKM法”可以说是一种结合DRM、RBF和非奇异一般解的边界建模技术。

[1]Gingold R A, Maraghan J J. Smoothed particle hydrodynamics: theory and applications to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(2): 375-389.

[2]Lancaster P,Salkauskas K.Surfaces generated by moving least-squares methods[J]. Mathematics of Computation, 1981, 37(155): 141-158.

[3]Liu WK, Jun S. Multiple-scale Reproducing Kernel Particle Methods for large deformation problems [J]. International Journal for Numerical Methods in Engineering, 1998, 41(7): 1339-1362.

[4]Chen W, Tanaka M. A meshless, integration-free, and boundary-only RBF technique [J]. Computers and Mathematics with Applications , 2002, 43(3-5): 379-391.

[5]Chen W, Tanaka M. New insights into boundary-only and domain-type rbf methods[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2000, 1(3): 145-151.

[6]Chen W, Hon YC. Numerical convergence of boundary knot method in the analysis of helmholtz, modified helmholtz, and convection-diffusion problems[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(15): 1859-1875.

[7]Kang S W, Lee J M, Kang Y J. Vibration analysis of arbitrarily shaped membranes using non-dimensional dynamic influence function [J]. Journal of Sound and Vibration, 1999, 221(1): 117-132.

[8]Kang S W, Lee J M. Free vibration analysis of arbitrarily shaped plates with clamped edges using wave-type functions [J]. Journal of Sound and Vibration, 2001, 241(1): 9-26.

[9]Chen J T, Chen I L, Chen K H, et al. A meshless method for free vibration analysis of circular and rectangular clamped plates using radial basis function [J]. Engineering Analysis with Boundary Elements, 2004, 28(5): 535-545.

[10]Leissa A W. The Free Vibration of Rectangular Plates[J]. Journal of Sound and Vibration, 1973, 31(3): 257-293.