Stability analysis of multi－time delay systems with controller failures based on switching approach

WANG Li－min， SHAO Cheng， JIANG Chong

（1.School of Control Science and Engineering，Dalian University of Technology，Dalian 116024，China；2.Department of Sports Information and Technology，Shenyang Sports University，Shenyang 110102，China）

Stability analysis of multi－time delay systems with controller failures based on switching approach

WANG Li－min＊1， SHAO Cheng1， JIANG Chong2

（1.School of Control Science and Engineering，Dalian University of Technology，Dalian 116024，China；2.Department of Sports Information and Technology，Shenyang Sports University，Shenyang 110102，China）

The issue of robustly exponential stability for a class of uncertain multiple time－varying delay systems with controller failures and nonlinear perturbations is considered.A switched uncertain multi－delay system model is utilized to describe the considered systems.A switching approach based on the average dwell time is employed for the switched system.A delay－dependent sufficient condition for robustly exponential stability of the switched system is established in terms of linear matrix inequalities by using the switching method.It is proved theoretically that the resulting closed－loop system is robustly exponentially stable even if controller failures are encountered.The effectiveness of the proposed method is also demonstrated by simulation example.

robustly exponential stability；controller failures；average dwell time；switched systems；linear matrix inequalities（LMIs）；multiple time－varying delays

0 Introduction

In some practical systems，it is frequently met to stabilize an open－loop unstable system.The controller inevitably fails over some time intervals due to some known or unpredictive cases.Therefore，the controller failure problem is expected to be a more important topic.In Lit.［1］，a methodology for the design of state feedback control is presented so that the closedloop system remains stable even when some parts of the controllers fail.In Lit.［2］，using a two－channel decentralized controller configuration，necessary and sufficient conditions are obtained for the existence of reliable controllers that maintain stability under possible failure of either of the two controllers for linear MIMO plants.According to the complete breakdown of the control signal（u（t）＝0），some results on linear time－invariant systems have been obtained based on the average dwell time method in Lit.［3，4］.But the papers mentioned above did not discuss the effect of delay.

Time－delays and perturbations are often encountered in practical control systems.Both of them are generally regarded as main sources of instability and poor performance of a control system.Considerable attention has been paid to the stability analysis and the controller design of the time－delay system［5－8］.Very recently，the timedelay systems have been extended to the switched systems［9－15］.In most of these papers，allsubsystems are either stable or unstable.Cases are frequently encountered where unstable subsystems have to be dealt with in some practice control systems，as is described in Lit.［16，17］.In Lit.［18］，a class of discrete constant time－delay switched systems with controller failure is considered by using average dwell time technique.However，no results are now available for such complex switched uncertain multi－time delay systems resulting from controller failures.

In this paper，robustly exponential stability analysis for a class of uncertain systems with multiple time－varying delays and both structure uncertainties and nonlinear perturbations is developed，whose controller fails from time to time due to physical or purposeful cases.The uncertain multi－time delay system subjected to controller failure is firstly modeled as a switched uncertain multi－time delay system including an unstable subsystem.By using the average dwell time approach combined with the integral inequality，under the conditions that the total activation time ratio of unstable subsystems to stable ones is upper bounded，with the help of the lemmas and a special piecewise Lyapunov function，a delay－dependent sufficient condition for exponential stability of the switched system is derived in terms of linear matrix inequalities.Finally，the effectiveness of the proposed method is demonstrated by simulation example.

1 Problem formulation and preliminaries

Consider the following uncertain linear system with multiple time－varying delays and nonlinear perturbations

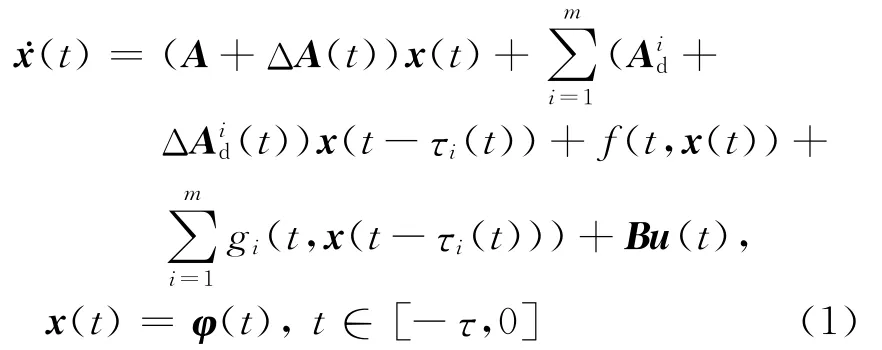
wherex（t）∈Rnis the state vector andu（t）∈Rmis the control input；A，（i＝1，2，…，m）andBare constant matrices of appropriate dimensions；the uncertaintiesΔA（t）and（t）（i＝1，2，…，m）are some perturbations with appropriate dimensions，and have the following forms：

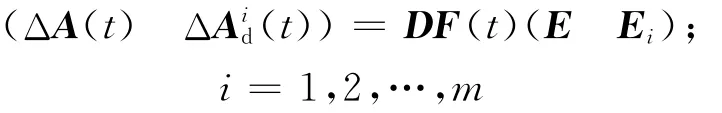
withFT（t）F（t）≤I，whereD，EandEiare known constant matrices with appropriate dimensions.The functionsf（t，x（t））andgi（t，x（t－τi（t）））（i＝1，2，…，m）are unknown nonlinear uncertainties.It is assumed thatf（t，0）＝0，gi（t，0）＝0（i＝1，2，…，m）and

where，for simplicity，f：f（t，x（t）），gi：gi（t，x（t－τi（t））），τi（t）（i＝1，2，…，m）are the timevarying delay of the system，and satisfy one of the following conditions：

WhereA（t）＝A＋ΔA（t）.Then，the entire system dynamics can be expressed as a switched system composed of an unstable subsystem and a stable subsystem.The form is expressed as

The objective of this paper is to design a class of switching laws under which System（5）is exponentially stable.To formulate the problem，some definitions and lemmas are introduced.

Definition 1［19］For each switching lawσand eachT≥t≥0，letNσ（T，t）denote the number of switching ofσover the interval（t，T）.If

τais called the average dwell time.

Definition 2System（5）is said to be exponentially stable if there exist scalarsλ＞0，κ＞1such that for allx（t）the following inequality holds：

Lemma 1［20］For any constant symmetric matrixW＞0，scalarτ＞0，and vector function（·）：［－τ，0］→Rnsuch that the following integral is well defined，then

Lemma 2［21］LetD，F，EandMbe real matrices of appropriate dimensions withMsatisfyingM＝MT，then for allFTF≤I，the fact thatM＋DFE＋ETFTDT＜0holds if and only if there existsε＞0such thatM＋ε－1DDT＋εETE＜0.

2 Main results

Due to System（3），the matrixAs＝A＋BKis stable，so a scalarλ－＞0can be obtained such thatAs＋λ－Iis stable.

Lemma 3 Under（H1），for givena＞0，bi＞0，λ－＞0and for allowable upper boundsτi＞0，if there exist positive symmetric matricesP1，，and positive scalarsε1，δ1，（i＝1，2，…，m）such that the following linear matrix inequality holds

Then，along the trajectory of System（3），it results in the following equation：

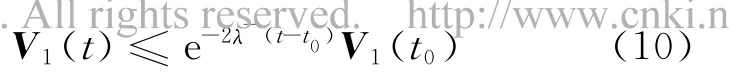
ProofChoose the Lyapunov－Krasovskii functional candidate

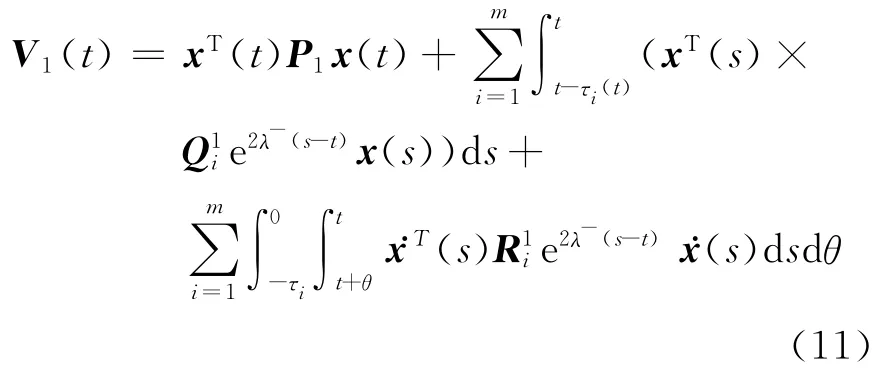
Then along the trajectory of System（3）and by Lemma 1together with Eq.（2），it leads to

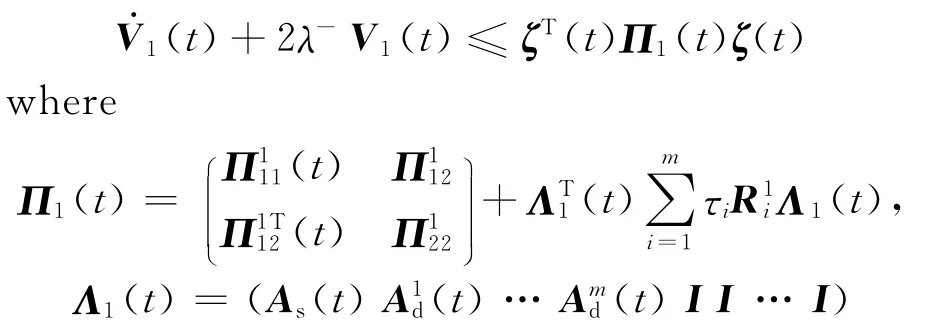
By Schur complements and Lemma 2，from Eq.（9）it is easy to see thatΠ1（t）＜0.Thus（t）＋2λ－V1（t）≤0.

Integrating the above inequality，it obviously holds that

When the controller fails，System（1）reduces to System（4）.As is well known，matrixAis unstable.There exists a constantλ＋＞0such thatA－λ＋Iis stable.The following resuls may be obtained.

Lemma 4Under（H1），for givena＞0，bi＞0，λ＋＞0and for allowable upper boundsτi＞0，if there exist positive symmetric matricesP2，and positive scalarsε2，δ2，（i＝1，2，…，m）such that the following linear matrix inequality holds

then，along the trajectory of System（4），it has

ProofSimilar to Lemma 3，choose the Lyapunov－Krasovskii functional candidate

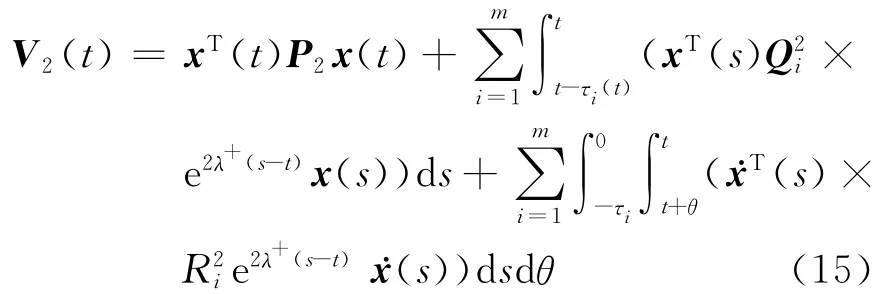
From the proof of Lemma 3，one can get

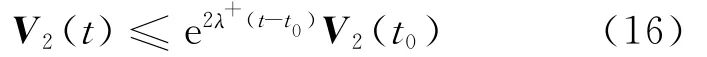
In the following section，the stability condition of switched System（5）is given based on the above two Lemmas.First，a class of switching laws is designed.

LetTuandTsbe the total activation time of the system（when the controller fails）and the system（when the controller works）during time interval［t0，t］，respectively，and choose a scalarλ＊∈（λ，λ－）.Forλ∈（0，λ－），consider a class of switching laws satisfying the following two conditions［16］：

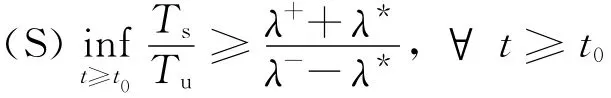
whereλ＋＞0andλ－＞0are to be chosen later.

Then，the following theorem can be obtained.

Theorem 1Consider switched Systems（5）satisfying（H1），for givena＞0，bi＞0and allowable upper boundsτi＞0，if there exist positive symmetric matricesPj，and positive scalarsλ－，λ＋，εj，δj，（j＝1，2）（i＝1，2，…，m）such that the following linear matrix inequalities（9）and（13）hold，then，the System（5）is robustly exponentially stable for any switching signal satisfying the conditions（S）and（T）.Moreover，the state of System（5）is given by

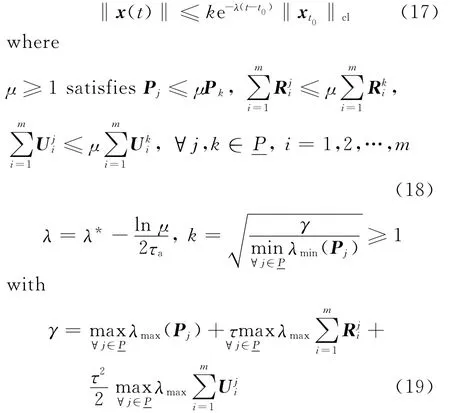
λmin（·），λmax（·）denote the minimum and maximum eigenvalues of a symmetric matrix，respectively.

ProofChoose the following piecewise Lyapunov－Krasovskii functional candidate

whereV1（t）andV2（t）are designed in Eqs.（11）and（15）.

From Eqs.（18）and（19），it is obvious that

Fort＞0，lett0＜t1＜…＜tk＝denote the switching points ofσover the interval（t0，t）.By using the differential theory and combining Eqs.（9），（13）and Lemmas 3，4，it leads to

It follows from Conditions（S），（T），Eqs.（21）and（22）that

From the definition of Lyapunov function together with Eq.（23），the following inequalities hold

Whereγis given in Eq.（19）.It follows from Eqs.（23）and（24）that

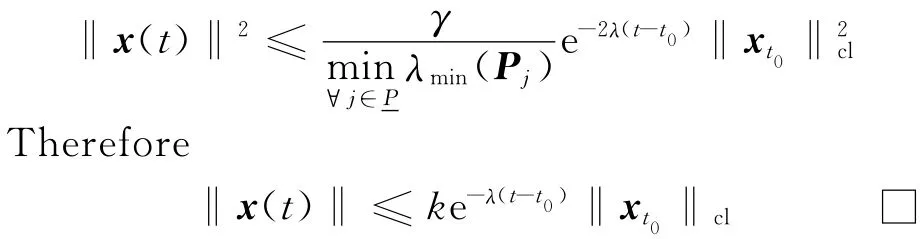
Remark 1It is obvious to see that there exist some parameters in Theorem 1.Here some parameters，for example，scalarsa＞0andbi＞0，are given in advance；some parameters，such as positive scalarsλ－andλ＋，are chosen with transcendental method；the upper bounds of time－delaysτiare obtained through the following method by giving proper choiceμi.

If the delay only satisfies（H2），by choosing＝0in Eqs.（9）and（13），Corollary 1is obtained.

Corollary 1Under（H2），for some given conditions in Theorem 1，if the following linear matrix inequalities（9）and（13）with＝0 hold，System（5）is robustly exponentially stable for any switching signals satisfying the Conditions（S）and（T）.

Remark 2Ifj＝1in Corollary 1，the system is non－switched uncertain system with multiple time－varying delays and nonlinear perturbations.So Corollary 1contains the existing results in Lit.［8］as a special case.

3 Numerical example

In this section，an example is used to illustrate the effectiveness of the proposed approach.

The state trajectory of the system during all over operation is shown in Fig.1in which the two subsystems are activated over time periods 0.3and 3.1respectively，where the initial condition isx0＝（－5 10）T.

From Fig.1，it can be seen that the system dynamics via switching are convergent quickly under the Conditions（S）and（T）.

By Corollary 1，h1，h2≤0.275is obtained if the derivative of delay is unknown.

Fig.1 The state response curves based on switching method

4 Conclusion

In this paper，robustly exponential stability analysis of switched uncertain multi－time delay systems is studied.Based on an average dwell time technique combined with linear matrix inequalities，it is shown that under a class of switching laws where the average dwell time is sufficiently large and the total activation time of the unstable subsystem is relatively small compared with that of the stable one，the switched uncertain systems with multiple time delays are robustly exponentially stable.Moreover，the derivative of the timedelay may allow to be any large or even unknown.At last，an example illustrates the effectiveness of the proposed method.

［1］SHIMEMURA E，FUJITA M.Control systems possessing integrity［J］.Transactions of the Society of Instrument and Control Engineers，1987，26：400－405

［2］GUNDES A N.Reliable decentralized stabilization of linear systems［J］.IEEE Transactions on Automatic Control，1998，43（12）：1733－1739

［3］ZHAI G S，TAKAI S，YASUDA K.Controller failure time analysis for linear time－invariant systems［J］.Transactions of the Society of Instrument and Control Engineers，2000，36（11）：1050－1052

［4］ZHAI G S，CHEN X K，SHIGEMASA T，etal.Stability and H∞disturbance attenuation analysis for LTI control systems with controller failures［J］.Asian Journal of Control，2004，6（1）：104－111

［5］HAN Q L.Robust stability for a class of linear systems with time－varying delay and nonlinear perturbations［J］.Computer and Mathematics with Applications，2004，47（8－9）：201－209

［6］CHEN Y，XUE A K，LU R Q，etal.On robustly exponential stability of uncertain neutral systems with time－varying delays and nonlinear perturbations［J］.Nonlinear Analysis：Theory，Methods ＆Applications，2008，68（8）：2464－2470

［7］JIANG X，HAN Q L.Delay－dependent robust stability for uncertain linear systems with interval time varying delay［J］.Automatica，2006，42（6）：1059－1065

［8］XIE N，TANG G.Delay－dependent nonfragile guaranteed cost control for nonlinear time－delay systems［J］.Nonlinear Analysis，2006，64（9）：2084－2097

［9］SUN X M，ZHAO J，HILL D J.Stability and H2－gain analysis for switched delay systems：A delaydependent method［J］.Automatica，2006，42（10）：1769－1774

［10］SUN X M，DIMIROVSKI G M，ZHAO J，etal.Exponential stability for switched delay systems based on average dwell time technique and Lyapunov function method［C］／／Proceedings of the American Control Conference.Minnesota：IEEE，2006：1539－1943

［11］SUN Y G，WANG L，XIE G M.Delay－dependent robust stability and stabilization for discrete－time switched systems with mode－dependent time－varying delays［J］.Applied Mathematics and Computation，2006，180（2）：428－435

［12］SUN Y G，WANG L，XIE G M.Delay－dependent robust stability and H∞control for uncertain discrete－time switched systems with mode－dependent time delays［J］.Applied Mathematics and Computation，2007，187（2）：1228－1237

［13］SUN Y G，WANG L，XIE G M.Stabilization of switched linear systems with multiple time－varying delays［C］／／Proceedings of the 45th IEEE Conference on Decision and Control.Piscataway：IEEE，2006：4069－4074

［14］KIM S，CAMPBELL S A，LIU X Z.Delay independent stability of linear switching systems with time delay［J］.Journal of Mathematical Analysis and Applications，2008，339（2）：785－801

［15］LIU J，LIU X Z，XIE W C.Delay－dependent robust control for uncertain switched systems with timedelay［J］.Nonlinear Analysis：Hybrid Systems，2008，2（1）：81－95

［16］ZHAI G S，HU B，YASUDA K，etal.Stability analysis of switched systems with stable and unstable subsystems：an average dwell time approach［J］.International Journal of Systems Science，2001，32（8）：1055－1061

［17］ZHAI G S，LIN H.Controller failure time analysis for symmetric H∞control systems［J］.International Journal of Control，2004，77：598－605

［18］SUN X M，ZHAO J，WANG R.State feedback control for discrete delay systems with controller failures based on average dwell time method［J］.IET Control Theory and Application，2008，2（2）：126－132

［19］LIBERZON D.Switching in Systems and Control［M］.Boston：Birkhauser，2003

［20］HAN Q L.A new delay－dependent stability criterion for linear neutral systems with normbounded uncertainties in all systems matrices［J］.International Journal of Systems Science，2005，36（8）：469－475

［21］YU K W，LIEN C H.Stability criteria for uncertain neutral systems with interval time－varying delays［J］.Chaos，Solitons and Fractals，2008，38（3）：650－657

1000－8608（2010）05－0794－07

基于切换方法的控制器故障下多时滞系统稳定性分析

王丽敏＊1， 邵 诚1， 姜 羽中2

（1.大连理工大学控制科学与工程学院，辽宁大连 116024；2.沈阳体育学院体育信息技术系，辽宁沈阳 110102）

研究了控制器故障下具有非线性干扰的多时变时滞不确定系统的鲁棒指数稳定性问题.利用不确定多时变时滞切换系统模型描述了所考虑的系统.提出了基于平均驻留时间的切换方法.在此方法下，以线性矩阵不等式（LMIs）形式得到了切换系统鲁棒指数稳定的充分条件，并从理论上证明了即使控制器失效所生成的闭环系统也是鲁棒指数稳定的.最后通过仿真算例验证了所提方法的有效性.

鲁棒指数稳定性；控制器失效；平均驻留时间；切换系统；LMIs；多时变时滞

TP13

A

2008－02－13；

2010－06－20.

“九七三”国家重点基础研究发展计划资助项目（2007CB714006）；辽宁省高校科研基金资助项目（L2010522）.

王丽敏＊（1976－），女，讲师，E－mail：wanglimin0817＠163.com；邵诚（1957－），男，教授，博士生导师.

by：2008－02－13； < class="emphasis_bold">Revised by

by：2010－06－20.

Supported by：National Grand Fundamental Research 973Program of China（Grant No.2007CB714006）；College Research Project of Liaoning Province in China（Grant No.L2010522）.

s：WANG Li－min＊（1976－），Female，Lecturer，E－mail：wanglimin0817＠163.com；SHAO Cheng（1957－），Male，Prof.，Supervisor of Doc..