双层金属腔体HEMP平面波孔缝耦合特性分析

柴焱杰,孙继银,孙东阳,胡 寅

（1.第二炮兵工程学院,西安 710025;2.西北核技术研究所,西安 710024;3.第二炮兵指挥学院,武汉 430012）

双层金属腔体HEMP平面波孔缝耦合特性分析

柴焱杰1,孙继银1,孙东阳2,胡 寅3

（1.第二炮兵工程学院,西安 710025;2.西北核技术研究所,西安 710024;3.第二炮兵指挥学院,武汉 430012）

高空核爆电磁脉冲（HEMP）对电子/电气设备构成严重威胁,是电磁兼容与电子/电气设备安全领域的重要研究内容。基于时域有限差分法（FDTD）的总场-散射场体系建立仿真空间,推导了连接边界的一维平面波引入方法,选择双层金属腔体为研究对象,仿真分析了腔体在HEMP平面波作用下透过孔缝在各采样点的响应过程。仿真结果显示,各采样点都出现了明显的振荡波形,其中外金属腔体孔缝中心比内金属腔体内部中心点耦合电场的峰值大;相同面积下,正方形孔、矩形孔的耦合电场比圆孔的耦合电场小;内部腔体与外部腔体在孔缝一侧距离的大小也会对耦合结果产生影响,间距越大,内部耦合电场的衰减越多。所得结论有利于指导双层金属腔体的电磁防护设计。

高空核爆电磁脉冲;平面波;时域有限差分法;孔缝;耦合

1 引 言

在核试验停止以后,采取理论研究和利用有限的实测数据进行数值模拟成为对核电磁脉冲环境更为切实可行的研究手段。文献[3]总结了国内外对核电磁脉冲环境研究的成果。屏蔽是电磁防护的重要手段,然而,为满足系统功能或散热需要,电子设备的各种屏蔽体不可避免地存在各种各样的孔缝,这些成为电磁脉冲能量耦合的重要通道。因此,评估各种金属腔体孔缝耦合的特性,是采取措施降低屏蔽体对电磁干扰耦合能力的必要前提。

本文以一种较为常见的双层金属腔为对象,使用时域有限差分（Finite Difference Time Domain,FDTD）法仿真计算双层金属腔体在HEMP平面波作用下的孔缝耦合特性,并对几种不同设置情况的计算结果进行总结。

2 HEMP波形标准及特性

当前,应用比较广泛的描述HEMP波形的标准有1976年出版物标准、Bell实验室标准和国际电工委员会（IEC）制定的HEMP标准等[4]。这些标准在对HEMP的描述中,一般将HEMP辐射波形拟合为双指数函数表达式。其中,IEC制定的HE MP标准波形为IEC定义的HEMP时域波形和归一化频谱如图1和图2所示。从图中可见,峰值达到50 000 V/m;上升时间和衰落时间分别是2.5 ns和55 ns;频谱分量覆盖了从中频（300 kHz～3MHz）以下,到高频（3～30MHz）、甚高频（30～300MHz）多个频段;波形能流分布的主要频段范围（能流比例在98%）是在100 kHz～100MHz之间[5]。因此,HEMP具有高峰值场强、快上升沿、宽频带等特点,对电子设备构成严重的威胁。

图1 IEC标准定义的HEMP波形Fig.1 HEMP waveform in IEC standard

图2 IEC波形的归一化频谱Fig.2 Relative amplitude in IEC waveform

3 使用FDTD法构建仿真空间

传统解析方法难以分析和计算复杂模型。时域有限差分法是研究电磁问题的一种重要的仿真数值计算方法,能够在时域直接计算得到宽带结果,适合于分析复杂电磁系统。以下是FDTD在x方向的迭代方程[6-7]:

式中,ε、σ、μ、σm分别表示介电常数（F/m）、电导率（S/m）、磁导系数（H/m）及导磁率（Ψ/m）,m表示与相应场分量处于相同位置的坐标信息。

仿真HEMP平面波激励源时使用总场-散射场（TF-SF）连接边界条件[8],如图3所示。其中,将受试设备（Interacting Structure）放置于总场区域的内部。

图3 FDTD总场/散射场计算模型Fig.3 TF-SF model of FDTD

根据等效原理,在连接边界上设置平面波的等效面电磁流,并设平面外的场为零,就可将入射波只引入到总场区。连接边界上的等效电磁流为

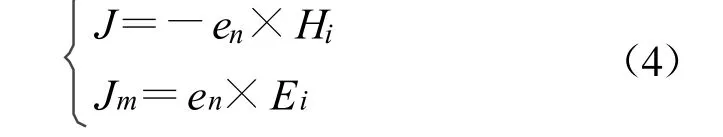
式中,en是面的外法向。

图9为电机运行在900 r/min时,突加和突减80%负载情况下,无延时补偿MPDTC、有延时补偿MPDTC和有延时补偿LSFMPDTC的定子磁链幅值|ψs|、转矩Te、转速n和电流isa.由图可以看出,有延时补偿MPDTC与LSFMPDTC的转矩脉动明显小于无延时补偿MPDTC的转矩脉动.3种控制方法的定子磁链幅值|ψs|在负载扰动时有微小的下降,而转速基本没有变化.

图4 HEMP平面波使用的球坐标系Fig.4 Sphere coordinate by HEMP p lane wave

通常使用球坐标系描述HEMP平面波激励源的传播方向和极化状态,如图4所示。其中 α是极化角。本文使用一维FDTD随时间逐步推进的方式提供连接边界上的切向场分量,以相对连接边界上角点延迟的思想解决任意角度平面波的引入问题[9]。一维FDTD平面波由式（5）表述:

其中k0是源点,一维FDTD场点的网格定义见图5,其时间步长、空间步长与三维FDTD计算空间相同。一维FDTD区域的左侧、右侧应留有若干网格以便加入吸收边界条件。

图5 一维FDTD场点Fig.5 Field points in 1-D FDTD

一维FDTD总长度L与总场空间（连接边界内的区域）有关,应满足条件:

式中,ZNX、ZNY、ZNZ是三维FDTD中总场空间3个方向上的长度,UNZ是一维FDTD吸收边界的厚度。

4 受试设备的物理模型

双层金属腔体的孔缝耦合模型见图6。内外腔体皆为立方体,材质为铜（电导率 σ=6.45×107s/m）。内腔体的边长为Lin=20 cm,外腔体的边长为Lout=30 cm;内外腔体孔缝一侧的间距为h,孔缝的形状和大小相同,位置始终正对;坐标系原点选择在外腔体一角,因此,内腔体的中心坐标为（15,h+10,15）,外腔体孔缝中心的坐标为（15,0,15）。HEMP平面波选择IEC标准波形,沿y轴传播,电场E为x轴方向,磁场H为-z轴方向。

图6 物理模型Fig.6 Physical model

5 仿真计算与分析

5.1 孔缝形状不同时HEMP平面波耦合特性

选择面积相同的正方形（6 cm×6 cm）、圆形（半径3.39 cm）、矩形（12 cm×3 cm）3种孔缝形状,如图7所示。

图7 3种孔缝形状Fig.7 Three kinds of apertures

使内腔体位于外腔体的中心,各面间距相同,此时h=5。图8显示了3种孔缝形状在（15,0,15）、（15,15,15）坐标点的电场Ex波形。

从图8（a）、（c）、（e）可以看出,外金属腔的孔缝中心的场强峰值较大,为80

0～1 200 V/m量级。在主峰值之后出现了与腔体壁反射波叠加生成的合成振荡波形,并由于腔体的损耗逐渐趋于零。正方形孔和圆形孔的峰值比矩形孔的峰值脉宽窄;矩形孔的宽边与HEMP的极化方向一致,耦合波形与入射波形类似,但幅值较小。

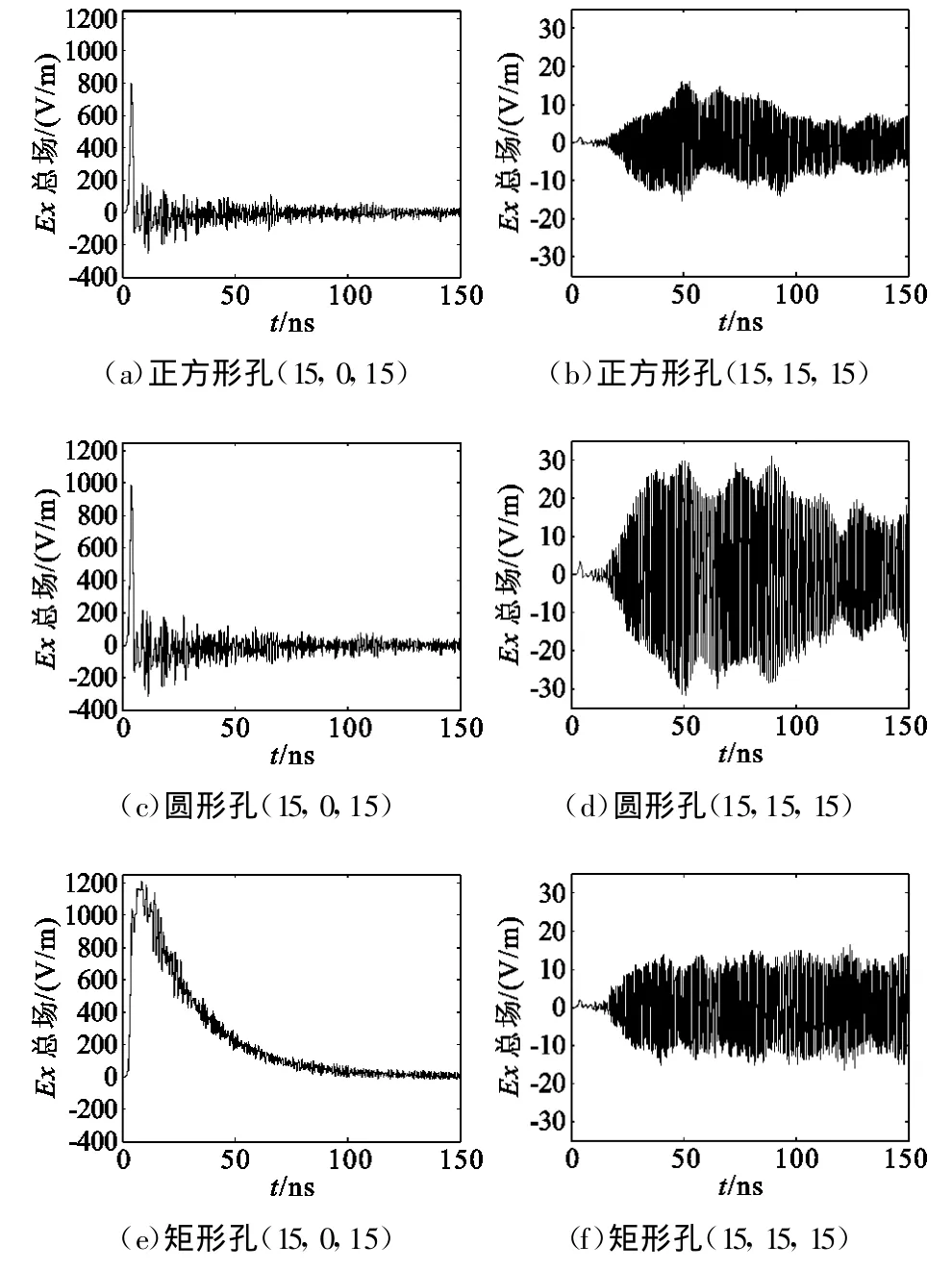
图8 3种孔缝的耦合电场Ex波形Fig.8 Coupling Ex waveforms of three kinds of apertures

图8（b）、（d）、（f）显示,HEMP平面波经过孔缝的耦合,在金属腔内来回振荡,双层金属腔体内部中心点耦合场强的峰值明显变小。其中,正方形孔和矩形孔的峰值较小,而且正方形孔的衰减趋势比矩形孔的明显,圆形孔的峰值较大一些。

5.2 内外腔体孔缝间距不同时HEMP平面波耦合特性

选择上例中的正方形（6 cm×6 cm）,沿y轴方向改变内腔体在外腔体中的中心位置,即设置h分别为2.5 cm、7.5 cm。图9（a）显示了h=2.5 cm时在（15,0,15）、（15,12.5,15）坐标点的电场Ex波形;图9（b）显示了h=7.5 cm时在（15,0,15）、（15,17.5,15）坐标点的电场Ex

波形。

本算例是追踪在孔缝间距不同的情况下,在外金属腔体孔缝中心和内金属腔体内部中心的场强变化。通过仿真计算,将图9与图8（a）、（b）相比较可以发现,外腔体孔缝中心耦合电场的波形在改变内外腔体孔缝间距时受到的影响不大,保持了相似的波形和幅值,但内金属腔体中心位置的耦合场强则不然,随着间距h的不断加大,内部耦合场强衰减很快。

图9 内外腔体孔缝间距不同时的耦合电场Ex波形Fig.9 Coupling Ex waveforms with the change of distance between internal and external apertures

6 结 论

随着计算理论和计算机软硬件的发展,解决电磁安全问题可使用多种方法和技术[10-11],其中,时域有限差分法（FDTD）是解决电磁问题的一种主要的数值计算方法,能够直接在时域中完成复杂模型的场计算,在电磁工程的分析与设计中具有广泛的应用[12-14]。

由于高空核爆电磁脉冲（HEMP）对电子/电气设备构成严重威胁,因此开展有关电子/电气设备HEMP效应的研究是很迫切的。本文仿真计算了一种双层金属腔体结构在HEMP平面波作用下的孔缝耦合效应。首先,从时域波形和频谱特性两方面分析了HEMP标准波形的特点。之后,简要概述了FDTD的基本原理,使用FDTD的总场-散射场体系建立仿真空间,对使用一维平面波推进的方法引入HEMP平面波到连接边界的过程进行了推导,经仿真计算得出了一些有价值的结论。计算结果表明,由于金属壁的反射作用,内外采样点都出现了明显的振荡波形;外金属腔体孔缝中心比内金属腔体内部中心点耦合电场的峰值大;正方形孔、矩形孔的耦合电场比圆孔的耦合电场小;在正方形孔的情况下,改变内外腔体孔缝的间距会对内金属腔体内部中心点耦合电场造成明显的影响,间距越大内部耦合电场的衰减越多。这些结论有利于指导双层金属腔体的电磁防护设计。

[1] 赖祖武.强电磁脉冲的破坏效应及防护[J].电子科技导报,1997（11）:32-34.

LAI Zu-wu.Destroy Effects and Protection of EMP[J].Electronic Science&Technology Review,1997（11）:32-34.（in Chinese）

[2] 石蓝.雷达系统对强电磁脉冲的防护研究[J].无锡职业技术学院学报,2007,6（4）:50-52.

SHI Lan.Studies on EMP Protection of Radar System[J].Journal of Wuxi Institute of Technology,2007,6（4）:50-52.（in Chinese）

[3] 周璧华,陈彬,石立华.电磁脉冲及其工程防护[M].北京:国防工业出版社,2003.

ZHOU Bi-hua,CHEN Bin,SHI Li-hua.EMP and EMP Protection[M].Beijing:National Defense Industry Press,2003.（in Chinese）

[4] 谢彦召,孙培云,周辉,等.地面附近高空核爆电磁脉冲环境[J].强激光与粒子束,2003,15（7）:680-684.

XIE Yan-zhao,SUN Pei-yun,ZHOU Hui,et al.Highaltitude electromagnetic pulse environment over the lossy ground[J].H igh Power Laser and Particle Beams,2003,15（7）:680-684.（in Chinese）

[5] 谢彦召,王赞基,王群书,等.高空核爆电磁脉冲波形标准及特征分析[J].强激光与粒子束,2003,15（8）:781-787.

XIE Yan-zhao,WANG Zan-ji,WANG Qun-shu,et al.High altitude nuclear electromagnetic pulse waveform standards:a review[J].High Power Laser and Particle Beams,2003,15（8）:781-787.（in Chinese）

[6] 葛德彪,闫玉波.电磁波时域有限差分方法[M].2版.西安:西安电子科技大学出版社,2006.

GE De-biao,YAN Yu-bo.The finite differrence time domain method of electromagnetic[M].2nd ed.Xi′an:Xidian University Press,2006.（in Chinese）

[7] Allen Taflove,Susan C Hagness.Computational Electrodynamics:The Finite-Difference Time-DomainMethod[M].2nd ed.Boston:Artech House,2000.

[8] Dennis M.Sullivan.Electromagnetic Simulation Using the FDTD Method[M].Idaho:IEEE,2000.

[9] 王长清.现代计算电磁学基础[M].北京:北京大学出版社,2005.

WANG Chang-qing.Foudation of Computational Electromagnetism[M].Beijing:Beijing University Press,2005.（in Chinese）

[10] 吕丹,童创明.部分涂敷目标的 RCS仿真计算[J].电讯技术,2010,50（4）:7-10.

LV Dan,TONG Chuang-ming.RCS Simulationof Partially Coated Targets[J].Telecommunication Engineering,2010,50（4）:7-10.（in Chinese）

[11] 刘旭东.基于DDS的毫米波汽车防撞雷达扫频源设计[J].电讯技术,2010,50（4）:61-64.

LIU Xu-dong.DDS-based Sweep Frequency Source Design for Millimeter Wave Automotive Collision Avoidance Radars[J].Telecommunication Engineering,2010,50（4）:61-64.（in Chinese）

[12] Frederick M Tesche,Michel V Ianoz,Torborn Karlsson.EMC Analysis Methods and Computational Models[M].New York:John Wiley&Sons,Inc.,1997.

[13] 郝新红,白钰鹏,何娟.高功率微波孔缝耦合特性的数值模拟及防护加固技术[J].探测与控制学报,2006,28（4）:34-38.

HAO Xin-hong,BAI Yu-peng,HE Juan.Numerical Studies on the Coupling Characteristics of HP M Pulse into Cavity with Slot and Protective Measures Against HP M[J].Journal of Detection&Control,2006,28（4）:34-38.（in Chinese）

[14] 陈修桥,胡以华,张建华,等.计算机机箱的电磁脉冲耦合模拟仿真[J].系统仿真学报,2004,16（12）:2786-2788.

CHEN Xiu-qiao,HU Yi-hua,ZHANG Jian-hua,et al.Simulation of Electromagnetic Pu lse Coupling with Computer Box[J].Journal of System Simu lation,2004,16（12）:2786-2788.（in Chinese）

Analysis of the Double M etal Cavities′Aperture Coupling by HEMP Plane Wave

CHAI Yan-jie1,SUN Ji-yin1,SUN Dong-yang2,HU Yin3
（1.The Second Artillery Engineering College,Xi′an 710025,China;2.Northwest Institute of Nuclear Technology,Xi′an 710024,China;3.The Second A rtillery Command College,Wuhan 430012,China）

High-altitude electromagnetic pulse（HEMP）poses a serious threat on the electronic/electrical equipment,which is an important research field of electromagnetic compatibility（EMC）and the security of electronic/electrical equipment.Computing model is built by the total-field/scattered-field of the finite difference time domain method（FDTD）,and 1-D plane wave method is imported in the connecting surface.Then,the apertures′response of double metal cavities under the HEMP plane wave is simulated and analysed using FDTD.The simulation results show that all samplesare showing clear oscillatory shape,and the peak electric field in aperture center of external metal cavity is larger than that of the center point of internal metal cavity.With the same aperture′s size,the internal coupling electric fields of the square aperture,rectangular aperture are smaller than that of circular aperture.The distance of the apertures between internal cavity and external cavity will also affect the coupling results,and the greater distance makes more attenuation of the internal coupling electric field.The conclusions are able to provide guidance for the protection design of double metal cavities.

high-altitude electromagnetic pulse（HEMP）;plane wave;FDTD method;slot;coupling

TP391.9

A

10.3969/j.issn.1001-893x.2010.11.024

1001-893X（2010）11-0114-05

2010-07-15;

2010-09-01

柴焱杰（1978-）,男,河北邯郸人,第二炮工程学院计算机应用技术专业博士研究生,主要从事电磁场数值计算与电磁脉冲效应研究;

CHAI Yan-jie was born in Handan,Hebei Province,in 1978.He is currently working toward the Ph.D.degree in the Second Artillery Engineering College.His research concerns numerically calculation and EMP effects.

Email:chaiyanjie2005@163.com

孙继银（1952-）,男,山东单县人,第二炮工程学院教授、博士生导师,主要从事多媒体信息处理、电磁脉冲效应研究;

SUN Ji-yinwas born in Shan County,Shandong Province,in 1952.He is now a professor and also the Ph.D.supervisor in the Second Artillery Engineering College.His research concerns multimedia disposal and EMP effects.

孙东阳（1981-）,男,吉林省吉林市人,2008年于西北核技术研究所获硕士学位,现为助理研究员,主要从事强电磁脉冲效应、电磁场数值计算研究工作。

SUN Dong-yang was born in Jilin,Jilin Province,in 1981.He

the M.S.degree in Northwest Institute of Nuclear Technology in 2008.He is now a research assistant.His research concerns EMP effects and numerical calculation.