运用斜面滑块模型探究牛顿第二定律

李铁

(锡山高级中学 江苏 无锡 214174)

笔者2008年在《物理通报》第6期，发表了《运用斜面滑块模型探究牛顿第二定律》[1]的文章，该实验方法以简单的实验操作，漂亮的实验结果让笔者着迷.2009年笔者以该方法参加江苏省创新大赛，并获得省创新大赛一等奖.根据评委们的意见，结合中学生的思维特点，我对该实验进行了认真的反思，对诸多实验环节进行了认真的修改.笔者认为，现在该实验的设计可以满足，原理简单、操作方便、结果准确的实验要求.

1 简单的实验原理

如图1，如果斜面倾角为β角时，小车沿斜面匀速下滑，则有

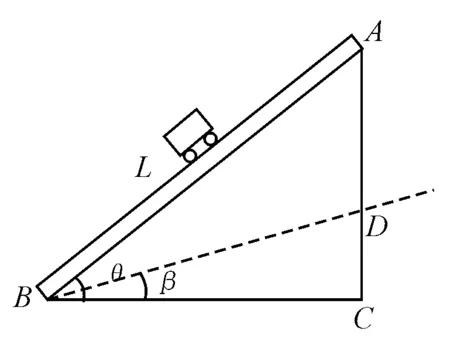
图1

μ=tanβ

(1)

当斜面倾角变为θ时，其受到的合力为

F=Mg(sinθ-μcosθ)=

(2)

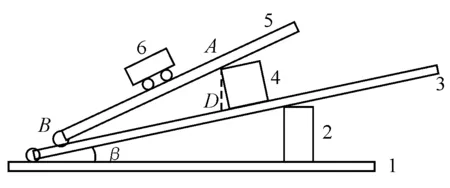
1.基板 2.垫块 3.中旋转基板 4.垫块

如图2，首先使中旋转基板3定位于图1中BD的位置.该操作可以借助数字毫秒计或打点计时器的监控完成.

(1)如图2，保持AB(如1 m)不变，分别放入三块直角垫块(边长分别为4×6×10 cm、8×12×10 cm、14×16×10 cm).改变AD的数值，用直尺测量出其数值，就可以得到成倍增加的合外力.

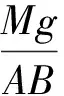
2 方便的实验操作

以探究牛顿第二定律为例.

(1)如图2，使中旋转基板3定位于图1中BD的位置，微调垫块2，通过打点计时器的监控，使小车6沿轨道5匀速下滑.

(2)如图2，取AB为1 m，放入直角垫块，用米尺测量AD出的数值.

(3)利用打点计时器与纸带测量小车加速度a.

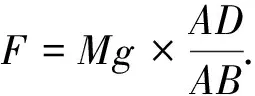
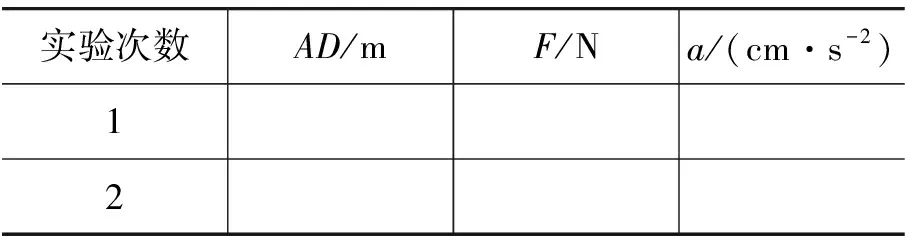
表1

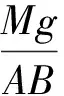
表2

3 实验结果

该实验设计由于不存在课本实验中实验原理不完善的系统误差，测量的数据范围大，加速度的数值大，偶然误差很小，其实验图线非常漂亮.下面是用上述实验原理完成的实验图像.

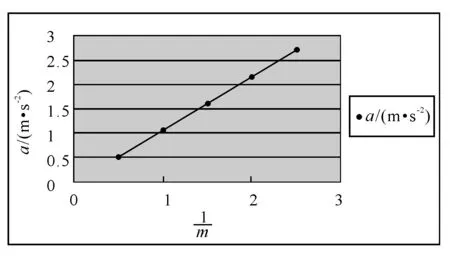
图3

实践是检验真理的唯一标准.课本实验尽管实验方法清楚，但多年来因为很难得到定量的实验结果，老师们已经将其弱化为定性实验；其繁杂的系统误差的分析，更让很多同学望而却步.本实验设计，其争论的焦点是，实验原理是否简单.其实，坐而论道是不科学的，还是让老师将该实验带进课堂，让老师的实践和同学的实践来回答.相信答案就在不远处.

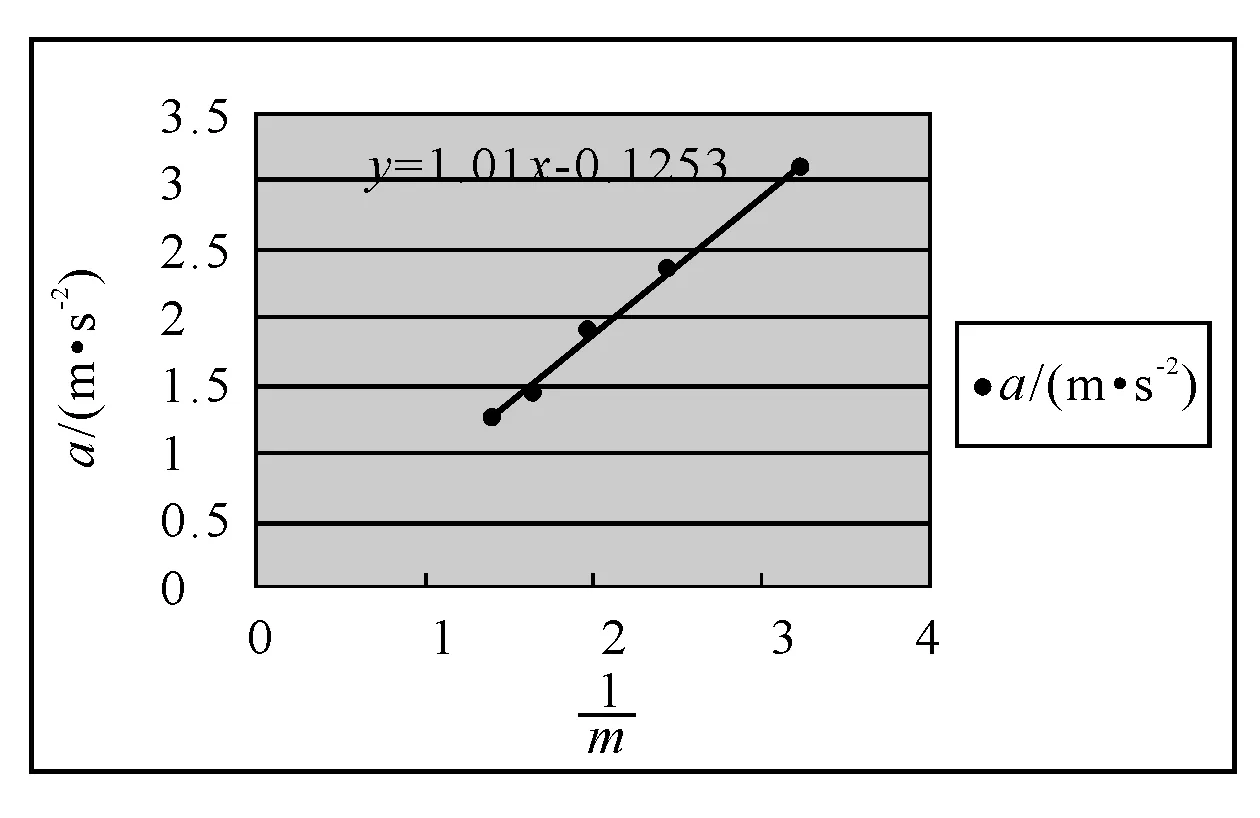
图4

1 李铁.运用斜面滑块模型探究牛顿第二定律.物理通报，2008(6)：31～33