对频谱及其几何意义的探讨
2010-01-26陈军
陈 军
(定西师范高等专科学校物电系 甘肃 定西 743000)
1 引言
频谱分析是信号与系统课程中最重要的内容之一.许多读者在学习中感到抽象,往往只能从数学上承认时域信号与它的频域(频谱)之间的变换关系,而没有深刻理解它的物理意义.利用Matlab软件可以帮助读者建立形象的几何概念达到真正掌握.
2 仿真实例
2.1 两个给定的共轭复信号频谱合成并生成对应的时域信号
首先来看欧拉公式,它是以最简明的方式建立了信号频域与时域的关系
它说明一个最简单的实余弦信号可以由正、负两个Ω0频率分量合成.在复平面上,正的Ω0对应于反时针旋转的矢量,负的Ω0对应于顺时针旋转的矢量.当这两个矢量的幅度相同,而相角符号相反时,就合成为一个在实轴上的矢量.它的相角为零,大小按余弦变化,形成了如图1所示的实信号cosΩ0t.由对称的正负频率合成.推而广之,任何实周期信号必然具有正、负两组频率的频谱成分,正、负频率频谱的幅度对称而相位反对称,或者说,是共轭的.
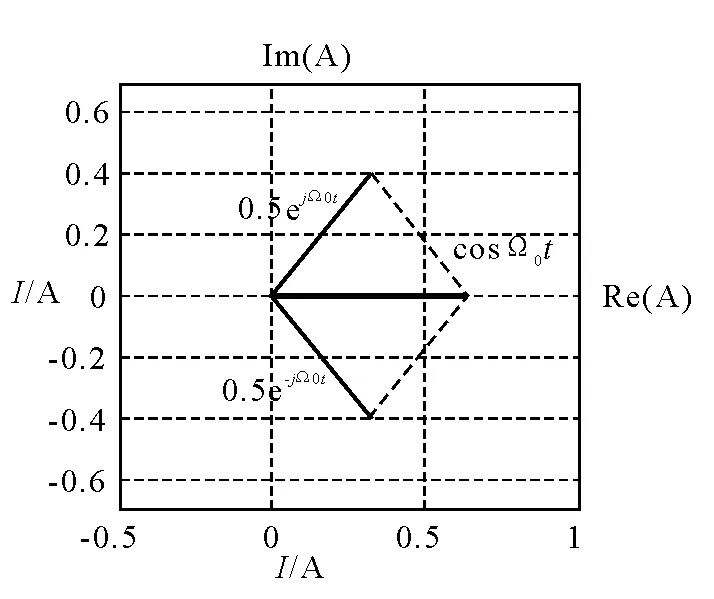
图1
可看出,任何虚周期信号也必然具有正、负两个频率的频谱成分,只是要把负频率的频谱矢量反号(这意味着使其幅度反号)后与正频率的频谱成分相加.这时两个矢量的幅度相等而相位互补,或者说,正、负两部分频谱的实部反号而虚部同号.这时的合成矢量在虚轴上,成为一个虚信号.
如果频谱不止这两项,而是有四项或更多呢?
2.2 四个任意给定的复信号频谱合成并生成对应的时域信号.
四项或更多频谱,它们的合成仍然可以用几何动画来表示.可以把每个频谱看作一根长度等于频谱幅度a(i)、按频率Ω(i)旋转的杆件,频谱的相加等价于多节杆件首尾相接,杆件末端的轨迹就描述了生成的时域波形.因为这个端点是在平面上运动,所以它将产生复信号,在实轴和虚轴上的投影分别为实信号和虚信号.
如设计一个以四个任意给定的复信号频谱合成并生成对应的时域信号的动态演示程序来说明.
2.2.1 建模 按上述多节杆合成模型
程序设计包括三个主要部分:1)各频谱分量的输入,包括其幅度和频率(有正负); 2)将各分量当作转动的杆件首尾相接; 3)记录多节杆系末端的轨迹画出图形.
2.2.2 Matlab程序(命名为eg)
% (1)给频谱矢量赋值
N=input(’N(输入矢量个数,为便于说明限定N不大于4)=’);
for i=I:N
i,a(i)=input(’振幅a(i)=’);
w(i)=input(’角频率w(i)=’);
end;
% (2)将各个频谱矢量相加合成并画图
t=linspace(0,20,201);It=length(t);
% 给出时间数组
p=a’*ones(1,It).*exp(j*w’*t);
% 各频谱分量随时间变化的复数值
q=cumsum(p);
% 各频谱分量的累加(包括所有节点)
figure(1),plot(real(q(4,:)),imag(q(4,:))),grid on
% 画合成复信号的端点轨迹
% (3)将此轨迹在实轴与虚轴两个方向的投影画成时间信号
figure(2),subplot(2,2,1),plot(real(q(4,:)),imag(q(4,:))),grid on
subplot(2,2,3),plot(real(q(4,:)),t),grid on % 画出实信号的时间波形
subplot(2,2,2),plot(t,imag(q(4,:))),grid on % 画出虚信号的时间波形
2.2.3 程序运行的结果
以五种情况的取值来阐明
第一种情况:运行eg程序并按提示输入,取如下四个幅度相等,频率符号等值的集总频谱,
a(1)=1,w(1)=1;
a(2)=1,w(2)=1;
a(3)=1,w(3)=1;
a(4)=1,w(1)=1;
则四个集总频谱的结果如图2中Figure(2)的P(b)和P(c)中,它分别显示正弦和余弦信号两种时域信号的情况,P(a)为两种信号的合成.
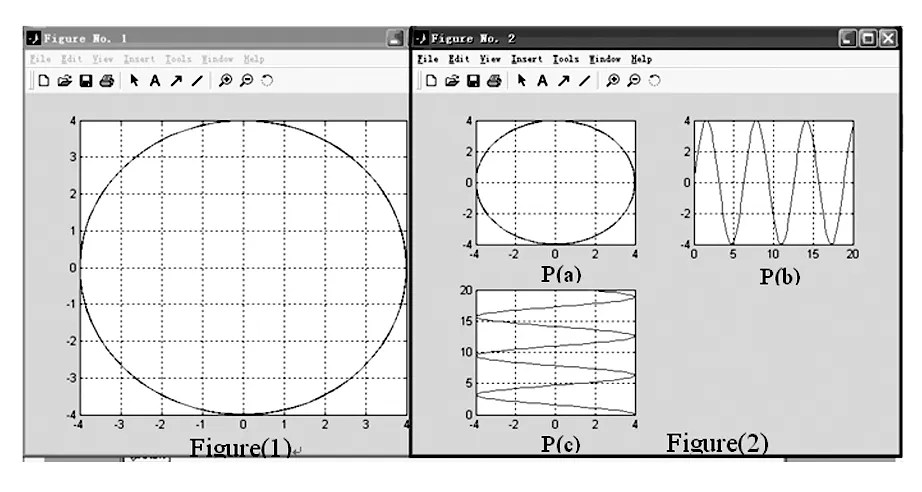
图2
第二种情况:只取如下两个幅度相等,频率符号相反等值的集总频谱,
a(1)=1,w(1)= 1;
a(2)=1,w(2)= -1;
a(3)=1,w(3)=2;
a(4)=1,w(1)= -2;
则四个集总频谱,输入则得到如图3的结果.

图3
第三种情况:如果只取两个幅度相等,频率符号相反等值的集总频谱,
a(1)=1,w(1)= 1;
a(2)=1,w(2)= -1;
a(3)=1,w(3)=2;
a(4)=1,w(1)=2;
则四个集总频谱,输入得到如图4的结果.
第四种情况:如下取两个幅度相等,频率符号相反不等值的集总频谱,
a(1)=1,w(1)= 1;
a(2)=1,w(2)= -1;
a(3)=1,w(3)=3;
a(4)=1,w(1)= -4;

图4
则四个集总频谱,输入得到如图5的结果.
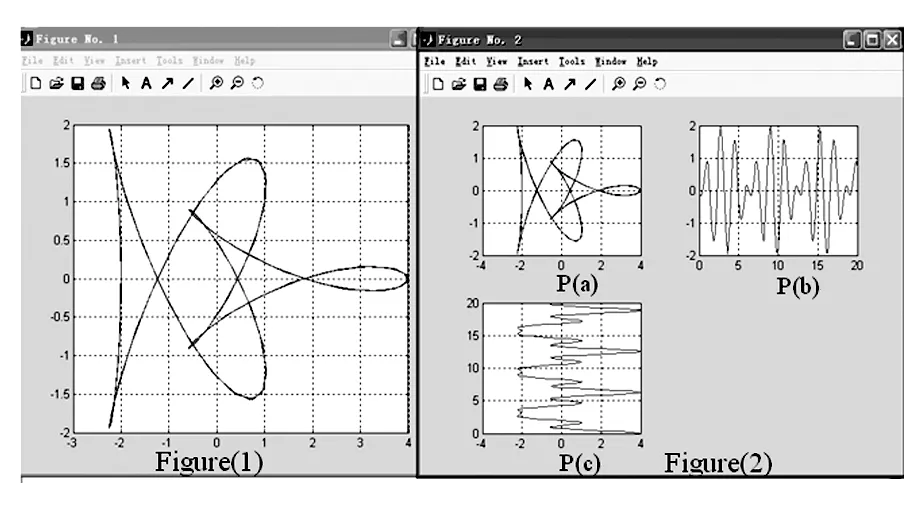
图5
第五种情况:如果取如下四个集总频谱,输入
a(1)=0.8,w(1)= 1;
a(2)=0.9,w(2)= -1;
a(3)=0.6,w(3)=2;
a(4)=0.5,w(1)= -3;
则得到如图6的结果.

图6
在图2、3、4、中显示了对称信号的合成,其输入频谱是对称的.其中图3有实信号而无虚信号;在图5、6中,为了显示复信号,有意把输入频谱设成不对称的.于是将看到四节杆件模拟的复信号的合成的运动动画,并得到杆系及其端点在复平面上的轨迹,它在x,y两方向的投影与时间轴的关系画在每幅图的Figure(2)的P(b)和P(c)中,我们就得到信号与系统课程中常见的实信号曲线.通过Matlab软件的模拟,使学习者轻松地理解频谱及其几何意义,化解教学难点.
输入频谱的幅度可以是负数,也可以是虚数,甚至可以是复数,它不仅反映了频谱的大小,还反映了该矢量的起始相位;频谱的频率则只能是可正可负的实数,正频率和负频率以及在该频率上频谱的意义在此不言而喻.学习者可以做各种各样的试验,例如当两组频率具有倍频关系时,得到的是周期信号,如果频率比是任意小数,那将得出非周期的信号;另外,这样的演示只适用于集总频谱,对于分布的频谱密度,就要把它想象为若干小的集总频谱的叠合.总之有了这样的形象演示,可以大大扩展时域信号与频域谱之间关系的思维空间.
3 结论
可见,只有在复信号平面上,才能看到频率的正负.负频率频谱的意义,打破了在实信号的局部范畴来思考问题而引起的限制.1992年联合国教科文组织在里约热内罗宣言中指出:纯粹数学与应用数学是理解世界及其发展的一把钥匙.从而使得人类真正认识这个世界,进而在这个世界中和谐生存发展.要在物理课堂教学中,灵活地运用数学成果及各种现代教育技术手段适时适量地运用多媒体技术,发挥其最大功效,就可以减轻学生学习的过重负担,提高课堂教学效率,培养学生非智力因素,有效地培养跨世纪的创造性人才.
参考文献
1 张谨,赫慈辉.信号与系统.北京:人民邮电出版社,1990.152~156
2 陈怀琛,吴大正,高西全.Matlab及在电子信息课程中应用.北京:电子工业出版社,2003.167
3 杨改学.现代教育技术教程.兰州:甘肃教育出版社,2001.258~260
4 Vinay K.K.Ingle,Joha G.Proakis.Digital signal Processing Using Matlab.BK&DK,1997.231
5 Sanjit K.K.Mitra.Digital Signal Processing:A Computer-Based Approach.Older Edition,2000.48
