卫星编队飞行姿态协同输出反馈控制

吕建婷,高 岱

(1.黑龙江大学数学科学学院,哈尔滨 150080;2.哈尔滨工业大学卫星技术研究所,哈尔滨 150001)

0 Introduction

Coordinated attitude control of Satellite formation is an active area of current research.Various strategies and approaches are discussed in many technical notes[1-9].These approaches may be divided into three separated categories which are leader-follower[1-2],behavioral[3-4]and virtual structure[5-6].In[1],a leader-follower strategy is applied in relative attitude control of a satellite formation using nonlinear control theory.In[4],the attitude control laws based on behavioral approach are developed.In[6],formation control ideas for multiple satellites using virtual structure approach are presented.Also these approaches can be classified into centralized and decentralized types.In[7],the authors gave a class of decentralized coordinated attitude controllers which guaranteed global convergence of the satellite formation.

One feature of all the aforementioned results is that no attention has been paid to output feedback con-trol and control saturation problems.Many control schemes adopt full state feedback controls that utilize both attitude and angular velocity measurements.But the assumption of availability of the angular velocity measurement is not always satisfied because of either cost limitations or implementation considerations.Therefore,the study of output feedback control[8-10]for attitude control of singlesatellite has become an active research topic.The main approach is the construction of a filter with appropriate attitude variables.In addition,one of the major problems in designing attitude control systems is the control input saturation.Whenever the saturation occurs in the input of the control system,the system’s dynamic performance goes bad or it may even cause the whole closed loop instable.Thecontrol input saturation in attitude control systems has been the focus on tremendous research effort over the years[10-11].

In[2],the authors presented a solution to the problem of tracking relative attitude in a leader-follower satellite formation without angular velocity measurements.In[12],theauthors used the auxiliary dynamical system to reach the control objective.In this paper,we design decentralized coordinated attitude output feedback control schemes.Without velocity measurements and assume that the attitude can be measured,two coordinated attitude control schemes are designed.The main approach is the construction of a filter.The second control scheme can solve not only output feedback problem but also the control input saturation by introducing hyperbolic tangent saturation function.Global asymptotical stability for the satellite formation is shown with Lyapunov analysis.

This paper is organized as follows.In section 1 we introduce system model.Coordinated attitude output feedback controller design approaches are presented in Section 2.Simulation results are provided in section 3,and finally conclusions are derived in section 4.

1 Satellites dynamics and problem formulations

The attitude dynamics for the ithrigid satellite can be expressed as

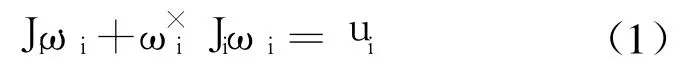
Where Ji∈ R3×3is the constant,positive-definite,symmetric inertia matrix,ωi=[ωi1ωi2ωi3]T∈R3is the angular velocity vector in the body frame with respect to the inertial frame,expressed in the body frame;ui=[ui1ui2ui3]T∈R3is the control torque;The notationζ×,∀ζ=[ζ1ζ2ζ3]T∈ R3denotes the following skew-symmetric matrix

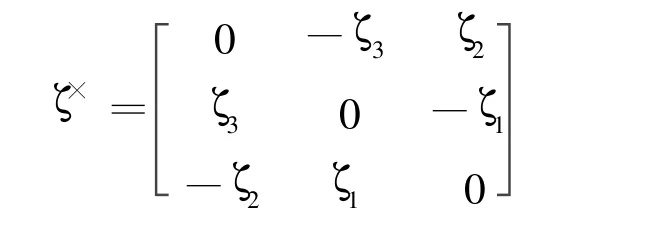
The attitude kinematics in term of the modified rodrigues parameter(MRP)takes the form

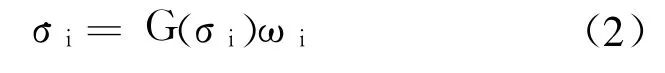
Whereσi=[σi1σi2σi3]T∈ R3represents MRP designating the attitude of the body frame with respect to the inertial frame,G(σi)∈ R3×3is given by the expression

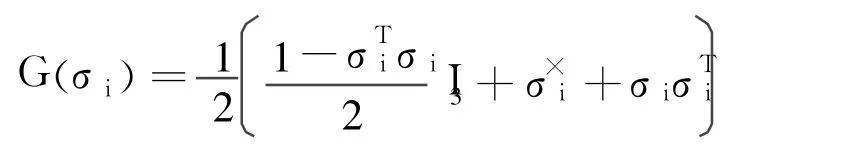
with I3denotes the 3×3 identity matrix.

The rotation matrix R(σi)in terms of MRPσican be depicted as

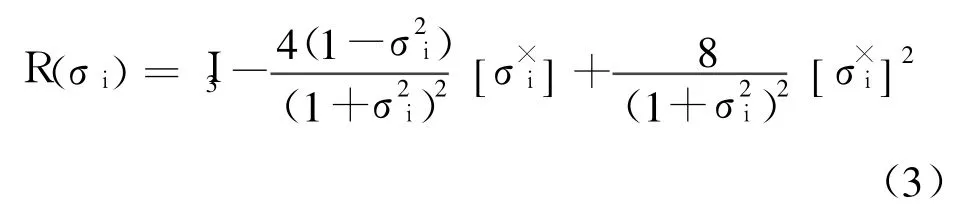
As shown in[13],it is possible to map the original MRPσto its corresponding shadow setσ*throughσ*=-(1/σTσ)σ.That is,by switching the MRPwheneverσTσ ＞ 1,one gets MRP bounded within unit sphere.

The attitude tacking error between the absolute attitude of the ithsatellite and the desired attitude is defined asand is governed by the following dynamics

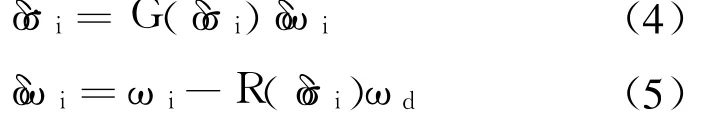
Whereδωiis angular velocity tracking error andωdis the desired angular velocity.

The relative attitude between the ithand jthsatellites is defined as

and is governed by the following dynamics

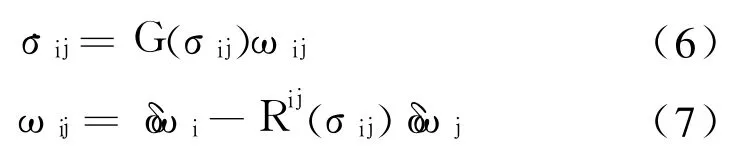
Whereωijis relative angular velocity.

In this paper the main objective is to design coordinated attitude output feedback control laws for satellite formation consisting of two satellites to solve the following problems

(1)To design a distributed attitude coordination control law subject to situation with unmeasurable angular velocity,which drives each satellite tracking the desired trajectory,and the relative attitudes and angular velocities converge to zero,simultaneously.

(2)To design a distributed attitude coordination control law subject to situation with control input saturation and unmeasurable angular velocity,which driveseach satellite tracking the desired trajectory, the relative attitudes,angular velocities converge to zero,simultaneously.

2 Controller design

In this section,two decentralized coordinated attitude control schemes for satellite formation flying consisting of two satellites without velocity measurements are designed.

First give the coordinated attitude output feedback control scheme by theorem 1.Global asymptotical stability for the satellite formation is shown with Lyapunov analysis.

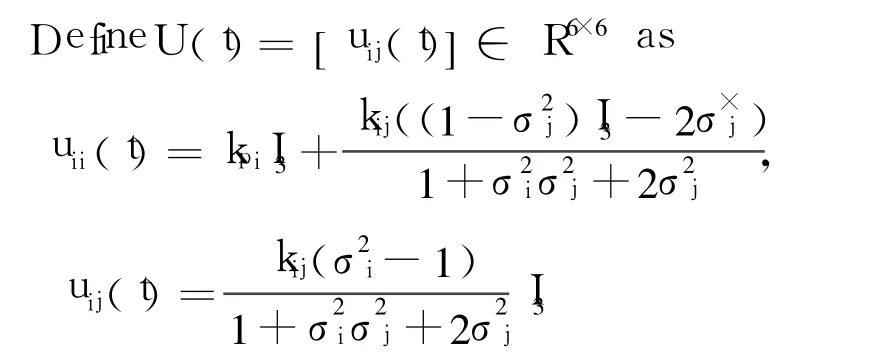
2.1 Coordinated attitude output feedback control

Theorem 1. For the system described by(1)～(7),if U(x)is full rank,there exists output feedback controller

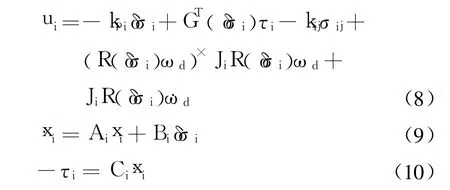
Such thattl→im∞(δσi,δωi,σij,ωij)=(0,0,0,0).

Where,Ai∈ R3×3is Hurwitz stable,Piand Qiare positivedefinite,symmetric matrix,kpi,kij＞0,kij=kji,i=1,2,j=1,2.

Proof. Consider the Lyapunov function candidate for the ithsatellite

After taking the time derivative of(11),the following

·expression for Vis obtained

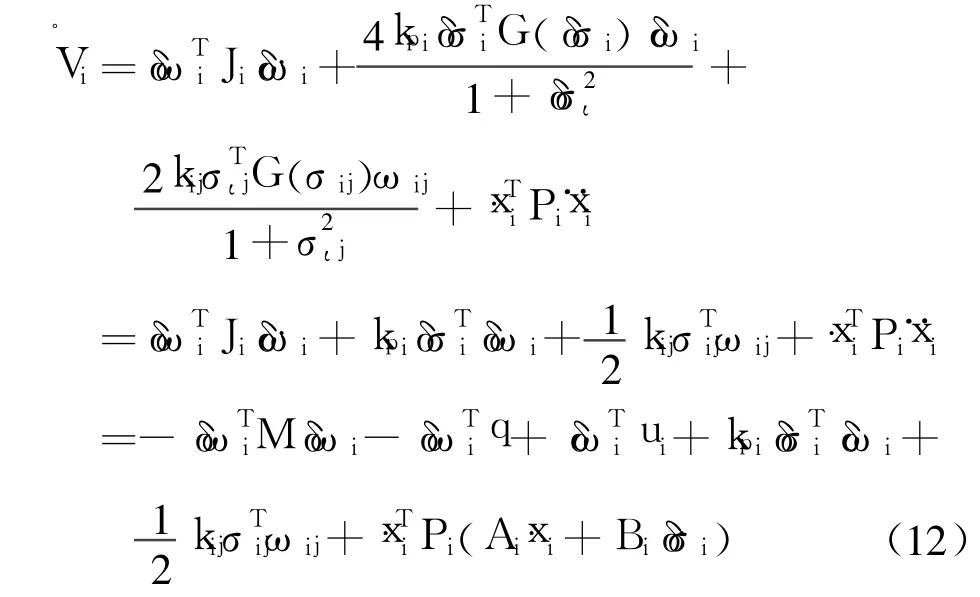
Where M=(R(δσi)ωd)×Ji+Ji(R(δσi)ωd)×,q=(R(δσi)ωd)×Ji(R(δσi)ωd)+Ji(R(δσi)ω˙d).

Because Jiis symmetric,(R(δσi)ωd)×is skewsymmetric,so we have M=-MT,andMδωi=0.Substitute them into(12),we get

Noteωij=-Rijωji,σij=-Rijσji,and kij=kji,then

Observe Fig 1～3 that the attitude tracking can be achieved.From simulation results,the proposed control scheme can achieve attitude coordination among the satellites and guarantee global asymptotical stability for the satellite formation.Simulation results show the proposed controller is effective.

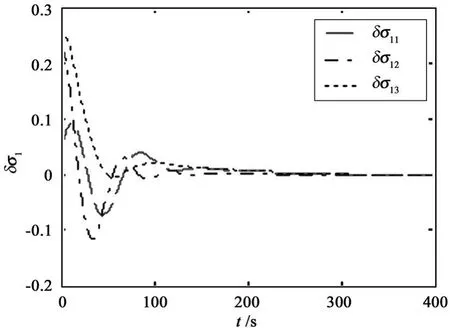
Fig.1 Time history of error MRP of satellite 1

4 Conclusions

We address the problem of coordinated attitude control of two satellite formation.Two output feedback control schemes are presented in terms of MRPvector.The second scheme can solve not only output feedback problem but also the control input saturation.Simula-tion results have demonstrated the effectiveness of the proposed control scheme.

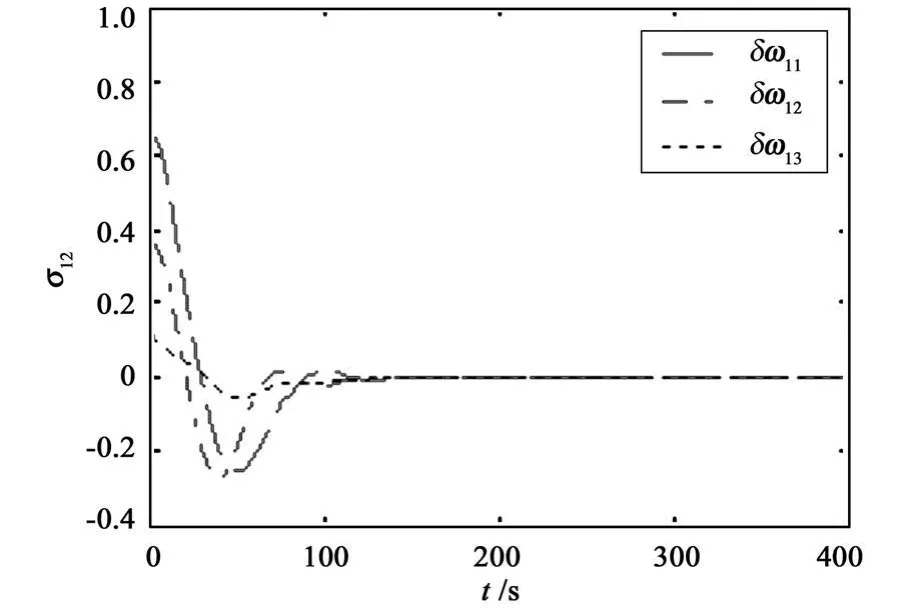
Fig.2 Time history of error angular velocity of satellite 1

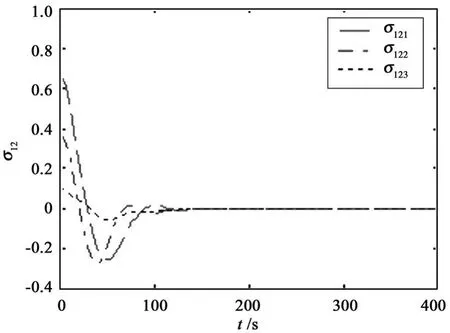
Fig.3 Time history of relative MRP

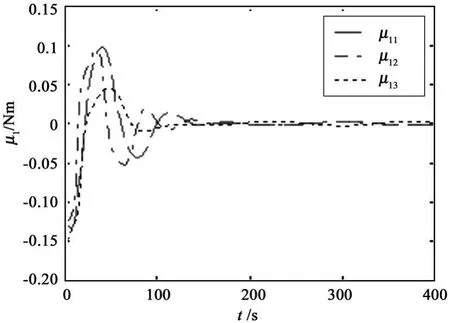
Fig.4 Time history of control torques of satellite 1

[1] Krogstad T R,Gravdahl J T.Group coordinated and cooperative control[M].Germany:Springer,2006:153-170.

[2] Kristiansen R,Loria A,Chaillet A,Nicklasson P.Spacecraft relative rotation tracking without angular velocity measurements[J].Automatica,2009,45(3):750-756.

[3] Lawton J,Beard R W,Hadaegh F Y.Elementaryattitude formation maneuvers via leader-following and behavior-based control[C].AIAA Guidance,Navigation and Control Conference and Exhibit,Denver Colorado,2000.

[4] Wang P,Hadaegh F,Lau K.Synchronized formation rotation and attitude control of multiple free-flyingspacecraft[J].Journal of Guidance,Control,and Dynamics,1999,22(1):28-35.

[5] Xin M,Balakrishnan SN,Pernicka H J.Position and attitude control of deep-space spacecraft formation flying via virtual structure andθ-D technique[J].ASME Journal of Dynamic Systems,Measurement,and Control,2007,129:689-698.

[6] Ren W,Beard R W.Decentralized scheme for spacecraft formation flying via the virtual structure approach[J].Journal of Guidance,Control,and Dynamics,2004,27(1):73-82.

[7] VanDyke MC,Hall CD.Decentralized coordinated attitude control within a formation of spacecraft[J].Journal of Guidance,Control and Dynamics,2006,29(5):1101-1109.

[8] Miwa H,Akella M R.Global adaptive stabilization using output feedback for spacecraft attitude tracking[J].Advances in the Astronautical Sciences,2002,112(1):345-356.

[9] Costic B T,Dawson D M,DeQuwieoz M S,Kapila V.Quaternion based adaptive attitude tracking controller without velocity measurements[J].Journal of Guidance,Control and Dynamics,2001,24(6):1214-1222.

[10] Akella M R,Valdivi A,Kotamraju G R.Velocity-free attitude controllers subject to actuator magnitude and rate saturations[J].Journal of Guidance,Control and Dynamics,2005,28(4):659-666.

[11] Boskovic J D,Li S M.Robust tracking control design for spacecraft under control input saturation[J].Journal of Guidance,Control and Dynamics,2004,27(4):627-633.

[12] Abdessameud A,Tayebi A.Decentralized attitude alignment control of spacecraft within a formation without angular velocity measurements[C].The 17th World Congress:the International Federation of Automatic Control,Seoul,Korea,July 6-11,2008.

[13] Schaub H,Robinett R D,Junkins J L.Globally stable feedback laws for near-minimum-fuel and near-minimum-time pointing maneuvers for a landmark-tracking spacecraft[J].Journal of Astronautical Sciences,1996,44(4):443-466.

[14] Slotine J,Li W.Applied nonlinear control[M].Englewood Cliffs,New Jersey:Prentice Hall,1991.