精度射击目标尺寸分析

王兆胜

(炮兵学院南京分院,南京211132)

精度射击目标尺寸分析

王兆胜

(炮兵学院南京分院,南京211132)

研究了在没有诸元误差及存在诸元误差两种情况下靶区圆目标和矩形目标的大小问题。从CEP的定义出发,讨论了不同密集度下圆目标半径的大小,运用对矩形目标的首发命中概率计算公式,分析了不同诸元误差和密集度下矩形目标的尺寸。得出的结论为:对圆目标,当不考虑诸元误差时圆目标的半径可取为0.50%X,当考虑诸元误差时圆目标半径可取为1.5%X;对于矩形目标,当不考虑诸元误差时,矩形区域的正面可取5mil,纵深1%X,当考虑诸元误差时,矩形目标尺寸的正面可设置为10 mil,纵深2%X。研究结果为精度射击试验与考核的目标设置提供了理论依据。

飞行器试验技术;目标,首发命中概率,密集度,诸元误差

间瞄火炮的射击精度可用射弹“进圈”或“进框”来直观地体现,目标的尺寸大小直接影响火炮对目标的命中概率。在火炮的战技指标精度试验、验收和考核射击中都有一个目标的设置问题,合理的目标尺寸应能体现火炮精度和炮手的训练水平。通常靶区目标可设置为圆目标或矩形目标,圆目标的大小由目标半径确定,矩形目标的大小由目标的正面尺寸和纵深尺寸确定,下面以首发命中概率满足50%来讨论靶区目标的尺寸问题。

1 圆目标尺寸的确定

从命中概率分析看,CEP是指弹着点落入半径r=CEP的圆内概率为 50%,也记为 R50[1]或R0.5[2-3],它是射击精度的圆概率误差指标。以目标中心为原点建立坐标系,x轴的正向为射击方向,z轴正向向右,以rm代表圆目标的半径,根据CEP的定义,可令rm=CEP,此时射弹对该圆目标的首发命中概率满足P=50%。下面分两种情况讨论圆目标的半径设置。

1.1 不考虑诸元误差的情况

设距离散布概率误差为Ex、方向散布概率误差为Ez,散布在x方向及z方向相互独立。散布为圆散布,即 Ex=Ez=E,当不存在诸元误差时,弹丸点围绕目标中心散布,此时CEP的计算公式为[4]:

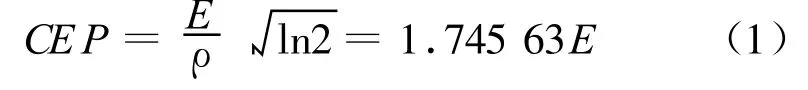
一般情况下火炮弹着点散布区域为椭圆,也即Ex≠Ez,此时CEP的计算公式为[5-6]:

求得了CEP即确定了圆目标的尺寸。因此,当不考虑诸元误差时,圆目标尺寸可取半径为rm=CEP。

根据式(2),不同密集度下圆目标半径如下:

当密集度为 Ex=X/220,Ez=1.2 mil时,CEP=0.493%X,因而可取目标半径 rm=0.493%X。

当密集度为 Ex=X/240,Ez=1.1 mil时,CEP=0.452%X,可取目标半径rm=0.452%X。

当密集度为 Ex=X/250,Ez=1.0 mil时,CEP=0.428%X,可取目标半径rm=0.428%X。

当密集度为 Ex=X/300,Ez=0.8mil时,CEP=0.354%X,可取目标半径rm=0.354%X。

根据密集度的战技指标及以上的讨论,圆目标的半径可取0.354%X～0.493%X。

根据以上的计算数据,在实际运用时,可考虑圆目标半径可统一取整为0.5%X。它适用于对密集度的评估。

1.2 考虑诸元误差的情况

火炮射击诸元误差是不可避免的,设诸元误差的距离概率误差为,诸元误差的方向概率误差为,距离散布概率误差为Ex,方向散布概率误差为Ez,根据公式(1)或(2),可分别得到诸元误差的圆概率误差CEPbi和散布误差的圆概率误差CEPpre,于是射击误差的圆概率误差CEPac为[5]:

2 矩形目标设置尺寸的确定

设矩形目标的正面为2lx,纵深为2lz,诸元误差的距离和方向概率误差分别为和,距离密集度为Ex,方向密集度为Ez,则对目标的首发命中概率为[8]:

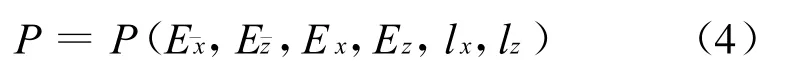
下面根据首发命中概率,分两种情况讨论矩形目标尺寸的大小。

2.1 不考虑诸元误差的情况

若不考虑诸元误差,当目标中心为瞄准点(即x0=0,z0=0),首发命中概率P的表达式为:

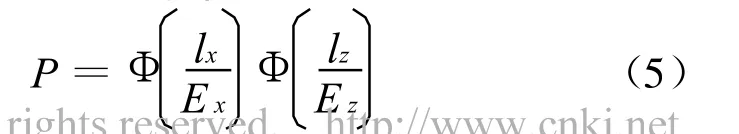
根据以上算式,当密集度为Ex=X/240,Ez=1.1 mil时,纵深可取2lx=1.30%X,正面可取2lz≈3.43 mil;

当密集度为Ex=X/250,Ez=1.0 mil时,纵深可取2lx=1.25%X,正面可取2lz≈3.12 mil;当密集度为Ex=X/300,Ez=0.8 mil时,纵深可取2lx=1.04%X,正面可取2lz≈2.50 mil。如果将目标尺寸进一步调整取整,取2lx=1%X,2lz=5 mil时,在以上3种密集度下首发命中概率都满足P＞0.5,因此在不考虑诸元误差的情况下,可将目标尺寸调整为纵深2lx=1%X,正面2lz=5 mil。

不存在诸元误差的情况下,尺寸为纵深2lx=1%X,正面2lz=5 mil的矩形区域可用于射击中对密集度的评估。

2.2 考虑诸元误差的情况

下面讨论存在诸元误差情况下矩形目标设置的尺寸,讨论以下几种目标尺寸。

1)纵深2lx=1%X,正面2lz=5 mil。

2)纵深2lx=1.5%X,正面 2lz=7.5 mil。

3)纵深2lx=2%X,正面2lz=10 mil。

4)纵深2lx=2.5%X,正面 2lz=12.5 mil。

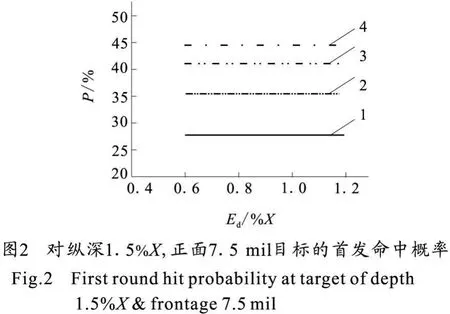
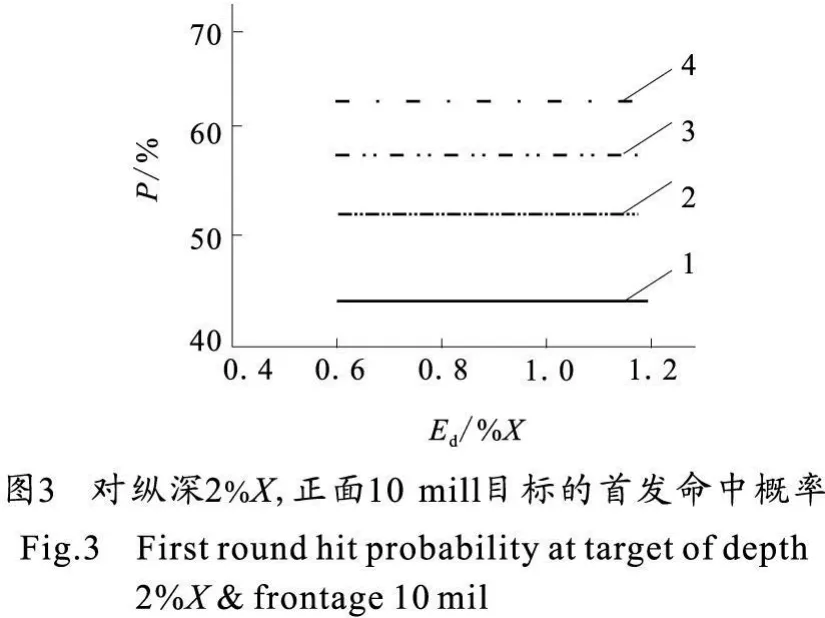
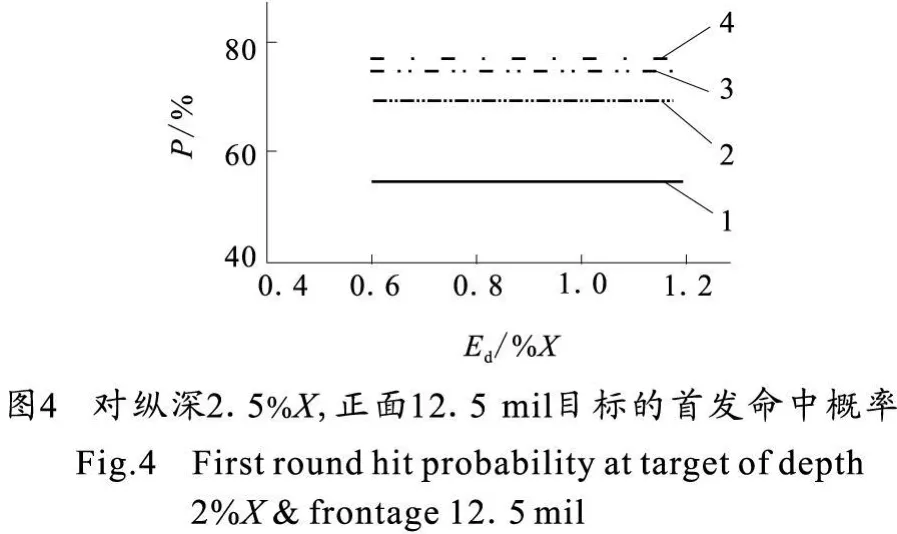
从图1、图2所示的计算结果看,在考虑诸元误差情况下对纵深为1%X、正面为5 mil及纵深为1.5%X、正面为7.5 mil的目标的首发命中概率都在50%以下;从图3所示的计算结果看,在考虑诸元误差情况下对纵深为2%X、正面为10 mil的目标,当密集度为Ex=X/200、Ez=1.2mil以上时对目标的首发命中概率均在50%以上;从图4所示的计算结果看,在考虑诸元误差情况下对纵深为2.5%X、正面为12.5 mil的目标的首发命中概率均超过50%。

3 结 论

根据以上对圆目标和矩形目标在两种情况下的计算结果,可得如下结论:

1)当目标设置为圆形时,如果不考虑存在诸元误差,根据密集度的战技指标,密集度试验圆目标的半径为0.354%X～0.493%X。根据计算数据,实际运用时圆目标半径可取为0.5%X。

3)不考虑诸元误差时,密集度试验矩形目标可设置为纵深2lx=1%X,正面2lz=5 mil。

4)考虑诸元误差情况下,由于纵深为1%X、正面为5 mil及纵深为1.5%X、正面为7.5 mil的矩形目标首发命中概率均达不到要求,而纵深为2.5%X、正面为12.5 mil的矩形目标首发命中概率指标又明显偏大,因此在目前的技术状态下,应取纵深取2%X、正面取10 mil的矩形目标作为射击精度试验的目标。

References)

[1]罗兴柏,刘国庆.陆军武器系统作战效能分析[M].北京:国防工业出版社,2007:84-85.

LUO Xing-bai,LIU Guo-qing.Operational effectiveness analysis of army armament[M].Beijing:National Defense Industry Press,2007:84-85.(in Chinese)

[2]文仲辉.战术导弹系统分析[M].北京:国防工业出版社,2000:122-126.

WEN Zhong-hui.Tactical missiles systems analysis[M].Beijing:National Defense Industry Press,2000:122-126(in Chinese)

[3]秦志高.陆基战略弹道导弹生存能力[M].北京:宇航出版社,1985:77.

QIN Zhi-gao.Survivability of land-based strategic ballistic missile[M].Beijing:Astronavigation Press,1985:77.(in Chinese)

[4]李延杰.导弹武器系统的效能及其分析[M].北京:国防工业出版社,2000:106.

LI Yan-jie.Effectiveness analysis for missile weapon systems[M].Beijing:National Defense Industry Press,2000:106.(in Chinese)

[5]徐明友.高等外弹道学[M].北京:高等教育出版社,2003:95.

XU Ming-you.Advanced exterior ballistics[M].Beijing:Higher Education Press,2003:95.(in Chinese)

[6]张廷良,陈立新.地地弹道式战术导弹效能分析[M].北京:国防工业出版社,2004:32.

ZHANG Ting-liang,CHEN Li-xin.Effectiveness analysis of surface to surface TBM[M].Beijing:National Defense Industry Press,2004:32.(in Chinese)

[7]郭锡福.远程火炮武器系统射击精度分析[M].北京:国防工业出版社,2005:120.

GUO Xi-fu.Firing accuracy analysis for long range gun weapon systems[M].Beijing:National Defense Industry Press,2005:120.(in Chinese)

[8]王兆胜.远程炮武器系统射击精度研究与射击精度战技指标论证[D].南京:南京理工大学,2003:101-103.

WANG Zhao-sheng.The study of firing accuracy and firing accuracy tactical&technical requirement reasoning for long range gunnery system[D].Nanjing:Nanjing University of Science&Technology,2003:101-105.(in Chinese)

Analysis on Target Sizes in Accuracy Firing

WANG Zhao-sheng

(Nanjing Artillery Academy of PLA,Nanjing 211132,Jiangsu,China)

T aking account of or taking no account of firing data error,the sizes of circular&rectangular targets in firing range were studied.From the view point of CEP definition,radius sizes of circular targets under different dispersions were discussed.By use of calculation formula of first round hit probability,sizes of rectangular targets in cases of different firing data errors and different dispersions were analyzed.There arrived at following conclusions:for circular targets,radius may be 0.5%X when firing data error was unconsidered,and 1.5%X when firing data error was considered;for rectangular targets,when firing data error was unconsidered,rectangular frontage may be 5mil and depth 1%X,when firing data error was considered,rectangular frontage may be 10mil and depth 2%X.The conclusions can provide the theoretical basis for target preparation in the examination process of accuracy firing and training evaluation.

experimental technology of aerocraft;target;first round hit prob-ability;dispersion;data error

TJ015

A

1673-6524(2010)04-0042-04

2010-01-23;

2010-03-18

王兆胜(1962-),男,教授,博士,主要从事自行火炮射击指挥教学与科研。E-mail:la_jin@126.com