内积H-Z-空间中的共轭Z-算子及其性质
2010-01-19秦宣华杨万必
秦宣华,杨万必
(湖北民族学院 理学院,湖北 恩施 445000)
文献[1]引入了Z-空间(X,+,θ,‖·‖)的概念,文献[2-5]引出了B-Z-空间、共轭Z-空间与共轭Z-算子,文献[6,7]引入了内积Z-空间与内积H-Z-空间 ,文献[8-10]引入了内积H-Z-空间中的正交投影、投影算子和一·五线性泛函的概念;在此基础上,本文提出了内积H-Z-空间中的共轭Z-算子的概念,并将泛函分析学中希尔伯特空间有关共轭Z-算子的性质移植到内积H-Z-空间之中.并讨论内积H-Z-空间中的共轭Z-算子的性质.
定义1 设H为内积H-Z-空间,T∈RZ(H),若存在T*∈RZ(H),使得(Tx,y)=(x,T*y)(∀x,y∈H),称T*为T的共轭Z-算子.
注:①由文献[10]知,对于任意连续线性算子T∈Rz(H),相应于T的共轭算子T*存在;②在文献[8,9]中讨论过内积H-Z-空间中的自共轭算子即满足T*=T的共轭Z-算子;③内积H-Z-空间中的自共轭算子也称为自共轭Z-算子或称为自伴Z-算子.
定理1 设H为内积H-Z-空间,A∈RZ(H),以下各结论等价:
(i)A是自共轭Z-算子;(ii)φ(x,y)=(Ax,y)是对称(Hermite)的.若H是复空间,则以上还等价于:
(ii)φ(x,x)=(Ax,x)为实数(∀x∈H).
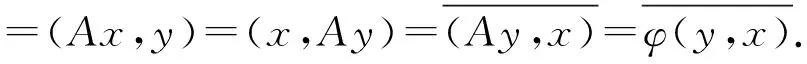
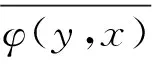
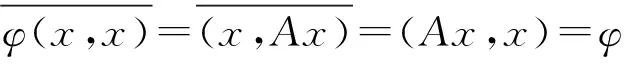
现在设H是复空间,证明(iii)⟹(ii).实际上利用极化恒等式可得到:
4φ(x,y)=4(Ax,y)=
(A(x+y),x+y)-(A(x-y),x-y)+i(A(x+iy),x+iy)-i(A(x-iy),x-iy)=
φ(x+y,x+y)-φ(x-y,x-y)=
φ(x+y,x+y)-φ(x-y,x-y)+iφ(x+iy,x+iy)-iφ(x-iy,x-iy).
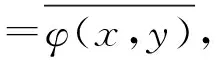
定理2 设H为内积H-Z-空间,T∈RZ(H)是自共轭Z-算子,则:

(1)

由T是自共轭Z-算子,计算可知:
(T(x+y),x+y)-(T(x-y),x-y)=2(Tx,y)+2(Ty,x)=2(Tx,y)+2(y,Tx)=4Re(Tx,y).
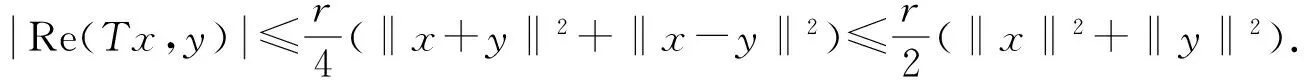
|(Tx,y)|=eiθ(Tx,y)=(T(eiθx),y)(‖eiθx‖2+‖y‖2)=(‖x‖2+‖y‖2).
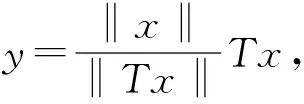
定理3 设H为内积H-Z-空间,A,B∈RZ(H),则:
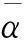

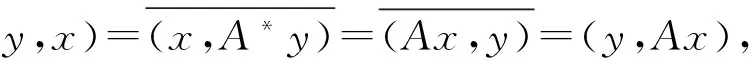
(iii)A,B∈RZ(H)故AB∈RZ(H),(AB)*存在.∀x,y∈H,(ABx,y)=(Bx,A*y)=(x,B*A*y),故(AB)*=B*A*.

[1] 王国俊,白永成.平移空间的线性结构[J].数学学报,2005,48(1):1-10.
[2] 杨万必,秦宣华.Z-空间上的线性算子的性质[J].中南民族大学学报;自然科学版,2006,25(1):97-99.
[3] 杨万必,李永亮.关于Z-空间的性质[J].湖北民族学院学报:自然科学版,2005,23(4):330-331.
[4] 杨万必.自然嵌入Z-算子与自反Z-空间及其性质[J].湖北民族学院学报自然版2007,25(3):330-331.
[5] 杨万必.共轭Z-空间与共轭Z-算子的性质[J].湖北民族学院学报:自然科学版,2008,26(1):12-14.
[6] 杨万必.内积Z-空间及其性质 [J].湖北民族学院学报:自然科学版,2008,26(3):330-331.
[7] 杨万必.内积H-Z-空间及其性质[J].湖北民族学院学报:自然科学版,2008,27(2):187-189.
[8] 秦宣华,杨万必.内积H-Z-空间中的正交投影及其性质[J]. 湖北民族学院学报自然科学版,2009,26(4):383-385.
[9] 秦宣华,杨万必.内积H-Z-空间中的投影算子及其性质[J]. 吉首大学学报:自然科学版,2009,30(5):21-25.
[10] 杨万必,秦宣华.内积H-Z-空间中的一·五线性泛函及其性质[J]. 湖北民族学院学报:自然科学版,2010,27(2):143-146.
[11] 刘培德.泛函分析基础[M].武汉:武汉大学出版社,2001:69-76,151-160,194-205.
