内积H-Z-空间中的一·五线性泛函及其性质
2010-01-18杨万必秦宣华
杨万必,秦宣华
(湖北民族学院 理学院,湖北 恩施 445000)
文献[1]引入了Z-空间(X,+,θ,‖·‖)的概念,文献[2~5]引出了B-Z-空间,文献[6]引入了共轭Z-空间与共轭Z-算子,文献[7]引入了内积Z-空间,文献[8] 引入了内积H-Z-空间;在此基础上,本文提出了内积H-Z-空间中一·五线性泛函的概念,并将泛函分析学中希尔伯特空间中一·五线性泛函的性质移植到内积H-Z-空间之中.本文首先介绍了共轭Z-空间与共轭Z-算子、内积Z-空间和内积H-Z-空间的概念;然后讨论了内积H-Z-空间中的一·五线性泛函的性质.
定义1[4]Z-空间X上的连续线性泛函的全体记为X*称X*是X的共轭Z-空间.
定义2[4]若X是Z-空间,X*的共轭Z-空间称为X的二次共轭Z-空间,记作X**.
定义3[4]若X是Z-空间,称算子J:X→X**,Jx=x**,x**(f)=f(x),∀f∈X*为从X到X**的自然嵌入Z-算子.
定义4[4,5]设X为Z-空间,J∶X→X**为自然嵌入映射.若J(X)=X**,称X为自反Z-空间.
定义5[4,5]设X是Z-空间,若∀x,y∈x,当x≠y,‖x‖=‖y‖=1时,
(1)
则称X为严格凸Z-空间.
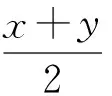
命题1[4,5]一致凸B-Z-空间是自反Z-空间.
命题2[4,5]B-Z-空间X是自反Z-空间当且仅当X*是自反Z-空间.
定义7[6]设X、Y为Z-空间,X*、Y*分别是X、Y的共轭Z-空间,T∈RZ(X,Y).若线性算子T*∶Y*→X*满足:
(T*y*)(x)=y*(Tx),∀x∈X,y*∈Y*.
(2)
则称T*是T的共轭Z-算子.
记f(x)=(f,x),则式(3)可以写成:
(T*y*,x)=(y*,Tx)
(3)
定义8[7]设(X,+,θ)是Abel群,Z是整数加群. 如果:
1)∀(m,x)∈Z×X,X中有唯一的元mx与之对应,且满足:
m(x+y)=mx+my;(m+n)x=mx+nx; (mn)x=m(nx);1·x=x;
其中m,n∈Z;x,y∈X.

则称(x,y)是x,y的次内积,称X为内积z-空间.
命题3[7]Z-空间(X,‖·‖)是内积Z-空间当且仅当∀x,y∈X,满足条件:
‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2).
(4)
定义9[8]完备的内积Z-空间称为Hilbert Z-空间,简称内积H-Z-空间.
命题4[9]若X是内积H-Z-空间,则X是一致凸Z-空间.
定义10[9]设H为内积Z-空间,E⊂H为线性子空间,x∈H.若存在分解x=x1+x2,其中x1∈E,x2⊥E,则称x1为x在E上的正交投影(简称投影),记为PEx=x1.
命题5[9]设H为内积Z-空间,E⊂H为线性子空间,y∈H,x1∈E,则以下诸条件等价:
1)PEy=x1;
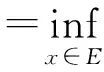
(5)
3)对于任何z∈E实变量函数f(λ)=‖y-x1+λz‖2在λ=0有最小值.
命题6[9](投影定理)设H为内积H-Z-空间,E⊂H为闭线性子空间,则∀y∈H,PEy存在且唯一.
命题7[9]设H是内积H-Z-空间,E⊂H是线性子空间,记E⊥={x∈H:x⊥E},则 :
1)E⊥是H的闭线性子空间;
2)若E是闭的,则E⊥⊥=E;
3)若E是闭的,则(Ei⊂Ei+1,i≥1),即H=E+E⊥,E∩E⊥={0};
4)若E是闭的,P∶H→E是投影算子,则E⊥=N(P).
定义11[10]1)设X为线性空间,T∶X→X为线性算子,若T2=T,则T称为幂等的.
2)设H为内积Z-空间,T∈R(H),若(Tx,y)=(x,Ty),∀x,y∈H,则T称为自共轭算子.
命题8[10]设H为内积H-Z-空间,P∈R(H),则下列诸条件等价:
1)P是投影算子;
2)P2=P并且P是自共轭的;
3)P2=P并且N(P)⊥R(P).
定理1 设H为内积H-Z-空间.
1)每个y∈H,f(x)=(x,y)是H上的连续线性泛函,并且‖f‖=‖y‖;
2)是H上的连续线性泛函,则存在y∈H,使得:
f(x)=(x,y) (∀x∈H),‖f‖=‖y‖.
(6)


注1:1)称定理1中的y为内积H-Z-空间中线性泛函f的表现;
2)记H上连续线性泛函的全体为H*,定理1表明从集合论的观点来看,H与H*是相同的.
定理2 设H为内积H-Z-空间,H*是H的共轭Z-空间.
1)若映射T∶H*→H,Tf=y,其中y是f的表现,则:
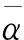
(7)
(称T为共轭线性的)T是到上的并且对于每个T∈H*,‖Tf‖=‖f‖.
2)(Tf,Tg)=(f,g),∀f,g∈H*.
(8)
3) 若J是从H到H*的自然嵌入算子,J是到上的线性映射,并且‖Jx‖=‖x‖(∀x∈H).

2°由‖T(f+g)‖=‖f+g‖‖T(f-g)‖=‖f-g‖,则:

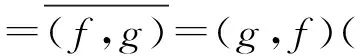
3°设J∶H→H**为自然嵌入算子,则∀x∈H,Jx(y)=y(x),(∀y∈H*).若x1,x2∈H,α,β∈ΦJ(αx1+βx2)(y)=y(αx1+βx2)=αy(x1)+β(x2)=αJx1(y)+βJx2(y)=(αJx1+βJx2)y,y是任意的.故J(αx1+βx2)=αJx1+βJx2.对于每个x**∈H**,由定理1,存在y*∈H*,使得x**(f)∈(f,y*)(∀f∈H*)并且‖x**‖=‖y*‖.若T是1°中的映射,不妨设Ty*=x,由2°知,x**(f)=(f,y*)=(Ty*,Tf)=f(x).故Jx=x**.J是到上的并且‖Jx‖=‖x**‖=‖y*‖=‖Ty*‖=‖x‖.所以结论成立.
注2:1)T∶H*→H是共轭线性的但不是线性的.因此按照线性同构的观念来看,当φ为复空间时,H*≠H,尽管H*与H之间存在一一的到上的映射,有时又特别地称H*与H是共轭线性同构的.
2)定理2(3)与一致凸Z-空间的结论是一致的,即内积H-Z-空间是自反Z-空间.
定义12 设H为内积Z-空间,映射φ∶H×H→φ.
1)若∀x,y,z∈H,α,β∈φ,φ(αx+βy,z)=αφ(x,z)+βφ(y,z),φ(αx+βy,z)=αφ(x,z)+βφ(y,z)
(9)
则称φ是一·五线性泛函;

3)若存在C>0,|φ(x,y)|≤C‖x‖·‖y‖,∀x,y∈H,则称φ是有界的.并且记:
‖φ‖=sup{|φ(x,y)|,‖x‖≤1,‖y‖≤1}.
(10)
定理3 设H为内积H-Z-空间,φ∶H×H→φ是有界一·五线性泛函当且仅当存在T∈RZ(H),使得:
φ(x,y)=(Tx,y)∀x,y∈H.
(11)
此时有‖φ‖=‖T‖.
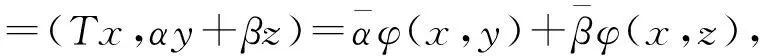
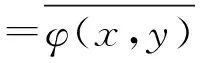


故‖T‖≤‖φ‖.
下面证明T是由φ唯一决定的.事实上,若另有T1使得(T1x,y)=φ(x,y)=(Tx,y),∀x,y∈H.则由y是任意的,必有T1x=Tx,再由x的任意性得到T1=T.总之由上述证明可知‖T‖=‖φ‖.
定理4 设H为内积H-Z-空间,则对于每个A∈RZ(H),存在唯一的B∈RZ(H),使得:
(Ax,y)=(x,By),∀x,y∈H.
(12)
证明令φ(x,y)=(x,Ay),则φ是一·五线性泛函,并且:
|φ(x,y)|=|(x,Ay)|≤‖x‖·‖Ay‖≤‖A‖·‖x‖·‖y‖.
φ是有界的.由定理3,存在B∈R(H)使得:
φ(x,y)=(Bx,y),
于是(Ax,y)=(x,By),交换x与y的符号即得(Ax,y)=(x,By).
[1]王国俊,白永成.平移空间的线性结构[J].数学学报,2005,48(1):1-10.
[2]杨万必,秦宣华.Z-空间上的线性算子的性质[J].中南民族大学学报:自然科学版,2006,25(1):97-99.
[3]杨万必,李永亮.关于Z-空间的性质[J].湖北民族学院学报:自然科学版,2005,23(4):330-331.
[4]杨万必.自然嵌入Z-算子与自反Z-空间及其性质[J].湖北民族学院学报:自然科学版,2007,25(3):330-331.
[5]杨万必.自反Z-空间与一致凸Z-空间的性质[J].吉首大学学报:自然科学版,2007,28(5):16-20.
[6]杨万必.共轭Z-空间与共轭Z-算子的性质[J].湖北民族学院学报:自然科学版,2008,26(1):012-014.060.
[7]杨万必.内积Z-空间及其性质[J].湖北民族学院学报:自然科学版,2008,26(3):330-331.
[8]杨万必.内积H-Z-空间及其性质[J].湖北民族学院学报:自然科学版,2008,27(2):187-189.
[9]秦宣华.杨万必.内积H-Z-空间中的正交投影及其性质[J].湖北民族学院学报:自然科学版,2009,26(4):383-385.
[10]秦宣华.杨万必.内积H-Z-空间中的投影算子及其性质[J] 吉首大学学报:自然科学版,2009,30(5):21-25.
[11]刘培德.泛函分析基础[M].武汉:武汉大学出版社,2001:69-76,151-160,194-205.
