区间二型模糊关系及其应用

陈一祥，刘丁酉

(武汉大学 数学与统计学院，湖北 武汉 430072)

1 区间二型模糊关系的概念及运算

当论域有限时，设U={u1,u2,…,um}，V={v1,v2,…,vn}，则U到V的区间二型模糊关系与一个矩阵相对应，这个矩阵称为区间二型模糊矩阵，它有如下形式：

由以上定义可知，区间二型模糊关系实际上就是区间值模糊关系，区间二型模糊矩阵实质上就是一个区间值模糊矩阵，这样命名的目的是希望和(区间)二型模糊集的理论统一起来.

区间二型模糊关系和一型模糊关系的不同之处在于前者用区间数来度量关系的程度的大小，下面先看一下区间数的有关运算.

引理1[4]设I1=[a1,b1]，I2=[a2,b2]是两个区间数，*∈{+,-,·,÷,∨,∧}，且当*是÷时，I2是无零区间数，则I1*I2也是区间数，且:

I1+I2=[a1+a2,b1+b2] ，I1-I2=[a1-b2,b1-a2]

I1∨I2=[a1∨a2,b1∨b2]，I1∧I2=[a1∧a2,b1∧b2]

I1·I2=[c,d]，其中c=min{a1a2,a1b2,b1a2,b1b2}，d=max{a1a2,a1b2,b1a2,b1b2}

特别地，当I1和I2为正区间数时，I1·I2=[a1b1,a2b2],I1÷I2=[a1÷b2,a2÷b1].对于数与区间数的运算，可以把数先表示成区间数的形式(即若a为实数，则a可表示成a=[a,a])，再按照区间数的运算法则进行.

在区间二型模糊关系中对关系程度的大小进行比较实际上就是对区间数的大小进行排序[5～8]，为此定义区间数的序关系.

定义2 设I1=[a1,b1]，I2=[a2,b2]是两个区间数，若有a1≤a2,b1≤b2，则称I1≤I2；若有a1≥a2,b1≥b2，则称I1≥I2；若有a1=a2,b1=b2，则称I1=I2.

根据区间数的运算及序关系可以定义区间二型模糊关系的运算.

类似于一型模糊关系的合成运算，可以定义区间二型模糊关系的合成.

当论域为有限时，区间二型模糊关系的合成可用相应的区间二型模糊矩阵的合成来表示.

易见，区间二型模糊关系的合成运算具有下列性质：

2 区间二型模糊相似关系和区间二型模糊等价关系

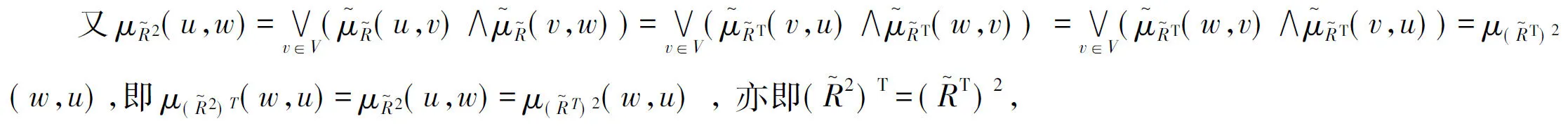
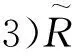
4)首先，由区间二型模糊关系复合运算的性质得：

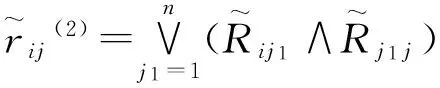
因此存在m≤n，使得:

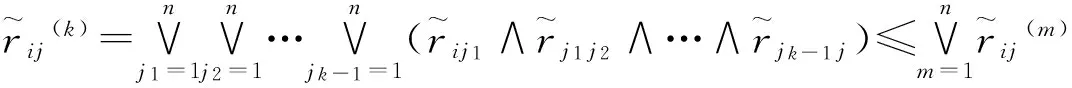
3 区间二型模糊等价关系在聚类中的应用

人的“相貌相似关系”是一个模糊关系，下面采用区间二型模糊集来刻画这一关系.假设要研究的对象是6个人，则论域U={u1,u2,u3,u4,u5,u6}，通过量化他们彼此的相貌相似程度得到区间二型模糊相似矩阵，不妨设为:

结果分析：上述例子表明，用区间二型模糊集来刻画模糊关系能够包含更多的模糊信息，对于不确定的模糊信息的度量，它不再用一个具体的数值而是用一个区间来表示，给出了不确定的范围，这更符合人类自然语言的本质.

[1]Dongrui Wu,Jerry M.Mendel. Uncertainty measures for interval type-2 fuzzy sets[J].Information Sciences,2007,177:5 378-5 393.

[2]Robert John,Jerry Mendel,Jenny Carter. The Extended Sup-Star Composition for Type-2 Fuzzy Sets Made Simple[C]//IEEE International Conference on Fuzzy Systems,2006:16-21.

[3]Yuh-Yuan Guh，Miin-Shen Yang，Rung-WeiPo，E.Stanley Lee.Inteval-valued fuzzy relation based clustering with its application to performance evaluation[J].Computers and Mathematics with Applications,2009,57:841-849.

[4]陈水利，李敬功，王向公.模糊集理论及其应用[M].北京：科学出版社，2005.

[5]Nakahara Y, Sasaki M, Gen M. On the linear programming problems with interval coeffiients[J].International Journal of Computer Industrial Engineering,1992,23:301-304.

[6]Senguta A, Pal T K.On comparing interval numbers[J].European Journal of Operation Research,2000,127:28-43.

[7]吴江，黄登仕.区间数排序方法研究综述[J].系统工程，2004,22(8)：1-4.

[8]李汶华,郭均鹏.判断矩阵的区间权向量及其方案排序[J]. 哈尔滨工业大学学报,2005,37(5):698-700.