两类正项级数敛散性判别法的改进及推广

曾 亮

(肇庆科技职业技术学院基础教学部,广东肇庆526114)

1 引 言

正项级数敛散性的判别方法有很多种,常见的有达朗贝尔比值判别法、柯西根值判别法、Raabe判别法、高斯判别法和对数判别法[1-3]等等,但每种判别法都其不足之处,也就是存在判别法失效的问题.近年来,学者们对正项级数敛散性的判别方法做了许多研究,提出了多种新的有效的判别法[4-11].本文将对其中两类作深入研究,得出它们的改进及推广形式,并通过实例验证其应用价值.

2 几个引理及定理

为了证明文中得出的定理,需下面的引理：

引理1[3]设为正项级数,且存在正数 N0,对一切 n＞N0,有则

(1)若∑νn收敛,则∑un也收敛;(2)若∑un发散,则∑νn也发散.

文献 [8]给出了Raabe对数判别法 (第二对数判别法),其表述如下:

引理2(第二对数判别法) 设∑a为正项级数 (a＞0),且则nn(1)当 l＞1时,级数∑an收敛;(2)当 l＜1时,级数∑an发散.

更一般地,可得到下面的判别法,其强弱依赖常数k,k越大判别法越强,越细致,所能判定级数的敛散范围也更宽.

则 (1)当 l＞1时,级数∑an收敛;(2)当 l＜1时,级数∑an发散.

文献 [9]中给出了一种新比值判别法:

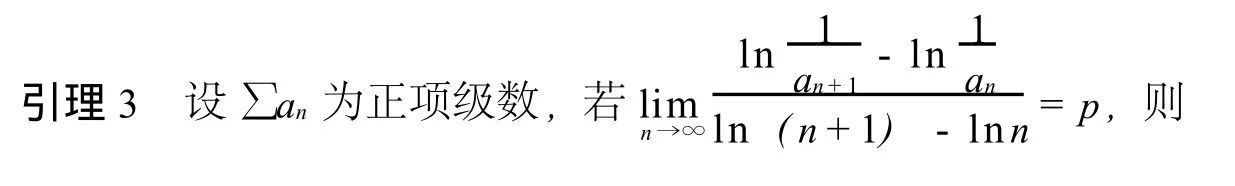
(1)当 p＞1时,∑an收敛;(2)当 p＜1时,∑an发散;(3)当 p=1时无法判断.

由于 p=1时,该判别法失效,为解决此问题,做如下改进:

当 l＞1时, ∑an收敛.

(2)当 l＜1时,则存在l＜p＜1,依上同理可证:∃N＞0,使得当 n＞N时有:

从而证得∑an发散.

更一般地,可得到下面的判别法,其强弱依赖常数k,k越大判别法越强,越细致,所能判定级数的敛散范围也更宽.

则(1)当 l＞1时,∑an收敛;(2)当 l＜1时, ∑an发散.

3 实际应用

分析与解答:本题利用引理2和引理3均无法判断 (因l=1,但利用定理1和定理3均可判断.

故由定理1知,级数

分析与解答:本题在文献 [3]中利用拉贝判别法无法判定,但利用文中的定理1和定理3均可判定.现利用定理1来判定.

[1] 徐森林,金亚东,薛春华.数学分析 (第三分册)[M].北京：清华大学出版社,2007：22-25

[2] (苏)吉米多维奇著,廖良文,许宁译.数学分析习题集 [M].合肥：安徽人民出版社,2005：230-268

[3] 华东师范大学数学系编.数学分析 (下册)(第二版)[M].北京：高等教育出版社,1991：8-19

[4] 李铁烽.正项级数判敛的一种新的比值判别法 [J].数学通报,1990,(01)：46-47

[5] 朱军.正项级数敛散性比值判别法的一种改进 [J].数学通报,1992,(05)：23-25

[6] 赵彦辉.正项级数的比值放大判别法 [J].西安建筑科技大学学报,1999,31(02)：185-188

[7] 马尔迈.关于正项级数比值判别法的一个推广 [J].浙江海洋学院学报：自然科学版,2003,22(04)：356-358

[8] 姬小龙,王锐利.正项级数的Raabe对数判别法 [J].高等数学研究,2007,10(03)：7-9

[9] 何国良.正项级数敛散性的两个判别法 [J].青海师专学报：教育科学,2005,(04)：34-36

[10] 刘启年.无穷级数比值判别法的推广 [J].荆州师范学院学报：自然科学版,2001,24(02)：25-26

[11] 祁建芳,刘一斐,董玉龙.有关收敛级数的两个问题 [J].河北北方学院学报：自然科学版,2006,22(02)：9-10