金融危机中企业受波及的数学模型的定性分析

吴庆华

(孝感学院数学与统计学院,湖北孝感 432000)

金融危机中企业受波及的数学模型的定性分析

吴庆华

(孝感学院数学与统计学院,湖北孝感 432000)

根据金融危机中企业受波及的无免疫型传染病模型,利用常微分方程的动力系统理论,对该模型进行了定性分析。得出了正平衡点的纵坐标是金融危机发生与否的临界值。

金融危机;波及;常微分方程;奇点;临界值

金融危机的发生和传播过程与传染病的发生和传播过程极其相似。谢德政[1]等首次利用传染病模型建立了金融危机中企业受到波及后及时调整,恢复常态后不再受波及的数学模型,即免疫型的数学模型。曹桃云[2]在前文的基础上,考虑了企业受到波及恢复常态后可能还会受到波及的情况,建立了无免疫型的数学模型。本文根据文献[2]提出的数学模型进行了修改,考虑了该系统的动力学行为。文献[2]建立了金融危机中受波及企业的无免疫型数学模型:

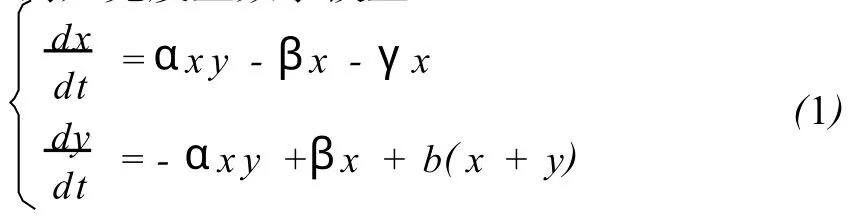
其中 x(t)表示t时刻正受到金融危机波及的企业数,y(t)表示t时刻易受到金融危机波及的企业数;α表示金融危机的波及率,β表示受到波及后的恢复率,γ表示受到波及后的倒闭率,b表示新批准企业率。自金融危机爆发以来,各国政府纷纷采取措施进行干预。但是干预的效果却不近人意,所以社会上对政府是否应该出手干预众说纷纭。下面在系统(1)的基础上加入政府干预项。

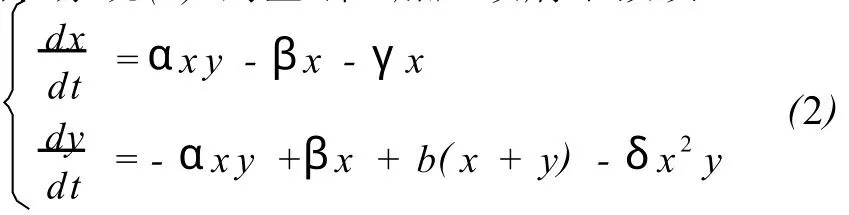
δ称政府干预系数,当金融危机发生时,政府会采取一定的宏观调控手段,使得易受波及的企业数随时间变化而减少。α,β,δ,γ,b皆为正常数。

1 模型分析

定理1系统(2)在第一象限内无闭轨。

证明取Dulac函数B(x,y)=xkym,k与m待定。则

取 k=m=-1,则 D=-(β+b)y-2。因为β＞0,b＞0,在第一象限内 y＞0,故 D ＜0。由Dulac准则,系统(2)在第一象限内无闭轨。

定理1说明金融危机不会周期性地发生。下面将分析系统(2)的平衡点的稳定性及平衡点附近的相图。

系统(2)有平衡点(0,0)和(x0,y0)=y0)是唯一的正平衡点。系统(2)在(0,0)点的线性近似为:

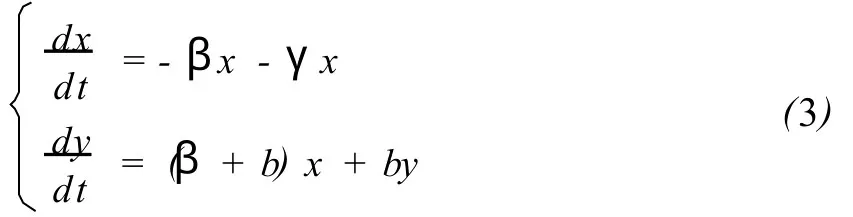
它的系数矩阵的特征根分别为λ1=-(β+γ),λ1=b所以(0,0)是不稳定的鞍点。

系统(2)在(x0,y0)点的线性化近似为

令方程(4)的系数矩阵 A的特征根为λ1,λ2,不难得出由(4) 式中的第一式可以得出,在上半平面 x(t)单调增加,下半平面x(t)单调减少,所以(x0,y0)不可能是双切结点。即只能是Δ≤0,所以得到下面的定理。

定理21)当Δ=0时,(x0,y0)是稳定的单向结点,轨线的相图如图1。

图 1 (Δ =0)

2)当Δ＜0时,是稳定的焦点,轨线的相图如图2。

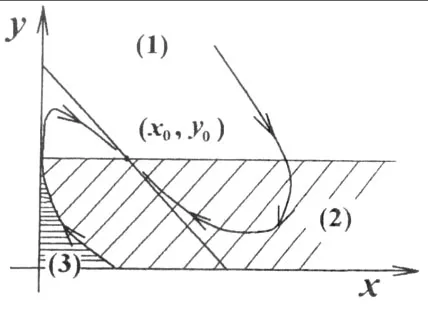
图2 (Δ ＜ 0)

相图1、2中的(1)区是金融危机爆发区,(2)区是危机缓解区,(3)区是危机解除区。

2 结论

1)金融危机不会周期性爆发,y0是临界值。当y(t)＞ y0时,即使 x(t)很小,随着时间推移,金融危机也会爆发;当y(t)＜y0时,即使x(t)很大,金融危机也很快会消失。

2)如果金融危机已经爆发,即初始时刻y(t0)＞y0,x(t)会先增大后减小。当y(t)=y0时,正受波及的企业数 x(t)最多,而是金融危机最终产生的破坏性影响的极限值。

3)减小b的值或者增加δ的值,会使x0减小。也就是说在金融危机已经发生时,减少新批准企业数,加大政府对企业的宏观调控可提高企业抗危机的能力,是控制金融危机的好办法。

[1] 谢政德,杨万年.金融危机中企业受波及的数学模型[J].数学的实践与认识,2007,3(37):1-3.

[2] 曹桃云.金融危机中企业受波及的数学模型[J].广州大学学报,2008,4(4):28-31.

[3] 王树禾.微分方程模型与混沌[M].合肥:中国科技大学出版社,1999.

Analysis of Mathematical Model of Enterprises Affected in Financial Crisis

WuQinghua
(School of Mathem atics and Statistics,Xiaogan University,Xiaogan,Hubei 432000,China)

In this paper,using the dynamical system s theory in the ordinary differential equation,we analyze the mathematical model of enterprises affected in financial crisis just as no-immune of infectious diseases.We conclude that the financial crisis will tend to some positive equilibrium and the ordinate of the positive equilibrium is the critical value of that financial crisis is broken out or not.

financial crisis;affect;ordinary differential equation;singular point;critical value

O175.1

A

1671-2544(2010)06-0021-02

2010-09-02

吴庆华(1977— ),女,湖北天门人,孝感学院数学与统计学院讲师,硕士。

(责任编辑:陈 鑫)