Dynamic Complexities in a Discrete Predator-prey System

ZHANG Li-min，LI Ling

（Dept. of Math& Finance-economics, Sichuan Univ. of Arts& Science, Dazhou Sichuan 635000, China）

Dynamic Complexities in a Discrete Predator-prey System

ZHANG Li-min，LI Ling

（Dept. of Math& Finance-economics, Sichuan Univ. of Arts& Science, Dazhou Sichuan 635000, China）

In this paper, the dynamic behavior of a discrete predator-prey system proposed in [2] is investigated for further study. Firstly, the conditions of existence for Hopf bifurcation are derived by using bifurcation theory. Secondly, the existence of chaotic behaviors in the sense of Marotto’s definition of chaos in certain conditions is proved. Finally, numerical simulations are conducted not only to verify the validity of the theoretical analysis but also reveal other complex dynamics behaviors such as period-doublings,period-halving bifurcations, attractor crises, quasi-periodicity, chaotic bands and periodic windows.

Hopf bifurcation; Marotto’s chaos; numerical simulation

1 Introduction

About the discrete predator-prey models, one of the early works was done by Beddington et al.[1]. After that, many authors have investigated the discrete predator-prey systems[2-6,10-16]. One important reason is that some species have no overlap between successive generations, thus discrete-time models are more realistic than continuous-time models to study these species. Another reason is that people always study population change by one year (month, week, or day) in practice, thus, it is important and necessary to obtain discrete systems from continuous population dynamical models , by which one studies their dynamical properties[9]. Recently, Zhang[2]proposed the following discrete predator-prey system:

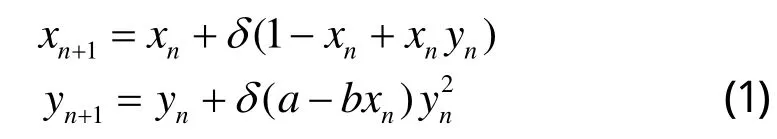
where is the integral step size. The more meaning of system (1) can refer to the reference[2]cited therein. It is shown in [2] that the system generates a flip bifurcation under some conditions.

In this paper, we continue to study system (1), to study its other dynamic behaviors, such as the existence of Hopf bifurcation and chaos. This paper is organized as follows. In the following section, we show that there exists Hopf bifurcation under some conditions. In Section 3, the existence of chaos in the sense of Marotto’s definition is proved. The numerical simulations are given in section 4.

2 Hopf bifurcation analysis

In this section, we establish conditions for the existence of Hopf bifurcation in system (1). Firstly, we introduce the following lemmas which are useful to establish our results

3 Existence of Marotto’s chaos

4 Numerical simulations

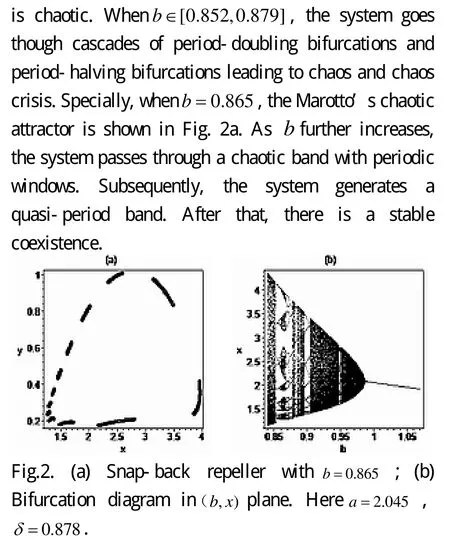
[1] Beddington JR, Free CA, Lawton JH. Dynamic complexity in predatorprey models framed in difference equations [J]. Nature, 1975, 255: 58-60.

[2] Zhang LM. Stability and bifurcation in a discrete predator-prey system with Leslie-Gower type [J]. Si Chuan University of Arts and Science Journal, 2010; 20 (2): 13-15.

[3] Celik C, Duman O. Allee effect in a discrete-time predator-prey system [J].Chaos, Solitons & Fractals, 2009, 40 (4): 1956-1962.

[4] Agiza HN, Elabbssy EM. Chaotic dynamics of a discrete prey-predator model with Holling type II [J]. Nonlinear Anal Real World Appl, 2009, 10:116-129.

[5] Liu Xl, Xiao DM. Complex dynamic behaviors of a discrete-time predator-prey system [J]. Chaos. Solitons & Fractals, 2007, 32: 80-94.

[6] Jing ZJ, Yang JP. Bifurcation and chaos in discrete-time predator-prey system [J]. Chaos, Solitons & Fractals , 2006, 27:259-277.

[7] Wiggins S. Introduction to applied nonlinear dynamical systems and chaos[M]. Berlin; Springer-Verlag, 1990.

[8] Marotto Frederick R. Snap-back repellers imply chaos innR[J]. Math Anal Appl , 1978, 63: 199-223.

[9] Zhang Y, Zhang QL, Zhao LC, Yang CY. Dynamical behavior and chaos control in a discrete function response model [J]. Chaos, Solitons &Fractals, 2007, 34: 1318-27.

[10] Francisco JS. Self-limitation in a discrete predator prey model[J]. Math Comput Model, 2008, 48: 191-196.

[11]Chen XX. Periodicity in a nonlinear discrete predator prey system with state dependent delays [J]. Nonlinear Anal Real World Appl, 2007, 8(2):435-446.

[12] Yang X. Uniform persistence and periodic solutions for a discrete predator prey system with delays [J]. J Math Anal Appl, 2006, 316:161-177.

[13] Fang N, Cheng X. Permanence of a discrete multispecies Lotka Volterra competition predator prey system with delays [J]. Nonlinear Anal Real World Appl, 2008, 9(5): 2185-2195.

[14] Chen FD. Permanence and global attractivity of a discrete multispecies Lotka Volterra competition predator prey systems [J]. Appl Math Comput, 2006, 181: 3-12.

[15] Xiao Y, Cao JD, Lin M. Discrete-time analogues of predator prey models with monotonic or nonmonotonic functional responses [J].Nonlinear Anal Real World Appl, 2007, 8(4): 1079-1095.

[16] Huo HF, Li WT. Stable periodic solution of the discrete periodic Leslie-Gower predator-prey model. Math Comput Model 2004, 40:261-269.

O175.7

A

1009－5160(2010)03－0036－05

一类离散捕食-被捕食系统的动力学复杂性

张莉敏，李 玲

（四川文理学院 数学与财经系，四川 达州 635000）

本文对文献[2]提出的一类离散捕食系统的动力学行为进行进一步研究. 首先利用分支理论，探讨了系统在一定条件下存在 Hopf分支；随后证明了系统在一定条件下存在 Marotto’s 混沌吸引子；最后利用数值模拟，不但验证了理论分析的正确性而且还揭示了系统其它动力学行为，例如：倍周期、到倍周期分岔，吸引子危机，拟周期, 混沌带和周期窗口.

Hopf 分支；Marotto’s 混沌；数值模拟

Biography：ZHANG Li-min (1982-), female, Lecturer, Research fields: Biological dynamics.

Supported by the National Natural Science Foundation of China (No.30970305), the Sichuan Provincial Education Department Scientific Research Project (No.TER2009-14)，the Sichuan Provincial Old Revolutionary Base Areas Foundation (No.SLQ2010C-17), and the Sichuan University of Arts and Science Natural Scientific Research Project (No. 2009B07Z).