北部湾潮汐潮流的数值模拟

徐振华, 雷方辉, 娄安刚, 曹圣山

(1. 中国海洋大学 数学系, 山东 青岛 266100; 2. 中海石油研究中心, 北京 100027; 3. 中国海洋大学 环境科学与工程学院, 山东 青岛 266100; 4. 中国海洋大学 海洋环境与生态教育部重点实验室 山东 青岛266003)

北部湾潮汐潮流的数值模拟

徐振华1, 雷方辉2, 娄安刚3,4, 曹圣山1

(1. 中国海洋大学 数学系, 山东 青岛 266100; 2. 中海石油研究中心, 北京 100027; 3. 中国海洋大学 环境科学与工程学院, 山东 青岛 266100; 4. 中国海洋大学 海洋环境与生态教育部重点实验室 山东 青岛266003)

基于正交曲线坐标的ECOMSED三维水动力模式, 对北部湾的潮汐潮流进行数值模拟。选用不同的海底摩擦系数、海底粗糙度系数以及水平湍流摩擦系数进行数值试验。试验结果表明, 当海底摩擦系数取 2×10-3～3×10-3, 海底粗糙度系数取 1×10-3～2×10-3m, 而水平湍流摩擦系数取 1×102～5×103m2/s时, 模拟所得潮汐、潮流结果与实测数据吻合较好; 并由此对北部湾的潮汐、潮流和潮余流等特征进行了分析。还给出了垂直湍流黏滞系数呈抛物型的分布特征。对该海域的水动力状况有了进一步的了解, 为该海域的环境保护规划提供了科学依据。

北部湾; 潮汐; 潮流; 数值模拟

北部湾是南海的主要海湾。夏华永等[1]在 1997年依经 Sigma坐标变换后具有自由表面的三维非线性 Navier-Stokes方程, 用分裂算子法对北部湾 M2和 K1分潮进行了三维潮流数值模拟, 孙洪亮等[2]在2001年利用 POM 三维水动力模式模拟了北部湾的潮汐、潮流特征, 殷忠斌等[3]在 1996年采用不同的参数对北部湾的 K1分潮进行了数值试验, 虽然北部湾的数值模拟工作开展得较为广泛, 但绝大部分工作都采用矩形网格, 并且网格都是均匀分布, 导致岸边界附近的流向很难与实际相符。作者基于二阶湍封闭模型的 ECOMSED三维水动力模式, 在北部湾建立了一个较为细致的正交曲线坐标系统, 并且对湾口处的网格进行加密, 垂向分为21层,可以更好地分析出各个物理量的垂直分布特征;采用不同的海底摩擦系数、海底粗糙度系数以及水平湍流摩擦系数进行数值试验, 并在此基础上, 分析出该海区潮汐、潮流和潮余流等特征, 以期对北部湾的水动力状况有进一步的了解, 并为制定该海域环境保护规划提供科学依据。

1 动力模式及其配置

作者所用的ECOMSED模式是由Blumberg等人在美国普林斯顿大学的三维海洋模式(POM)及其后来发展的河口、陆架和海洋模式(ECOM)的基础上发展而来的, 是一个较为成熟的集海浪和沉积输运为一体的浅海三维水动力学模式, 其中三维水动力模块从原始三维方程出发, 以自由水位、三方向速度分量、温度、盐度、密度以及代表湍流的两个特征量：湍动能和湍宏观尺度作为预报变量。关于此模块的特点和有关方程及其差分格式在Blumberg[4]2002年的有关文章中有详细叙述。

本文的计算范围为105.5°～111.5°E,15.5°～22.0°N。模式水平方向采用正交曲线网格, 网格空间步长最大为5 km; 垂向不等距分为21层, 采用σ坐标变换, 第一层取 0.007, 从而各物理量可以更好地逼近海表的物理场, 其余各层均匀分布。在模式中只考虑 M2和 K1分潮作为开边界的潮强迫条件, 其调和参数从海洋图集南海分册的同潮图内插得到; 模拟采用零初始条件, 计算选取的内模时间步长为134.631 s。为了保证计算的稳定性, 强迫的边界潮位从零开始逐步增加, 经过 3个潮周期后达到正常变化, 第四个潮周期后形成稳定的潮波。计算海区的水深分布及正交曲线计算网格分别见图1和图2。采用不同的海底摩擦系数、海底粗糙度系数以及水平湍流摩擦系数对北部湾的潮汐潮流进行数值试验。

图1 北部湾海底地形(单位：m)Fig. 1 The sea-floor topographic map in Beibu Bay(unit：m)

图2 北部湾正交曲线计算网格Fig. 2 Orthogonal curvilinear computation grids in Beibu Bay

2 有关参数的数值试验结果

作者用K代表海底摩擦系数,E代表水平湍流摩擦系数,C代表海底粗糙度系数。对于这3个参数分别进行试验。

对于K值, 以 1.25×10–3为间隔从 1×10–3到6×10–3取值。对于E值, 具体取值分别为：10, 1×102,5×102, 1×103, 5×103, 1×104, 5×104m2/s。表1 和表2是分别对应不同K值和E值的计算方案, 北部湾中几个计算点 K1分潮潮振幅和位相的变化, 点的位置见图1。结果分析发现, 当K取2×10-3～3×10-3,E取1×102～5×103m2/s时计算结果与实测结果比较符合,这与文献[3]基本一致。

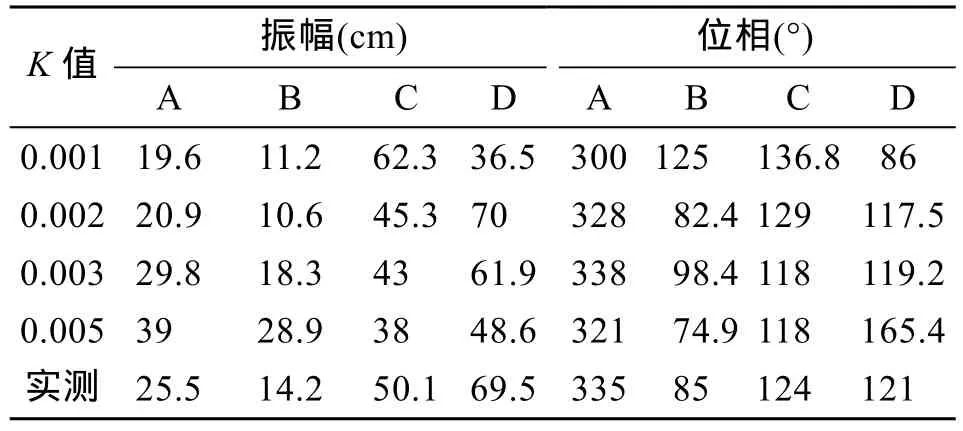
表1 不同K值K1潮汐要素的变化Tab. 1 Variation of the K1 tide at different values of K

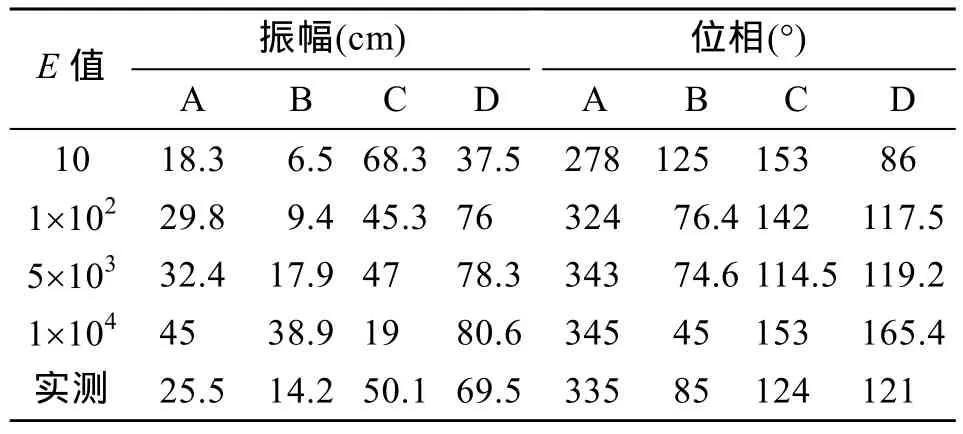
表2 不同E值K1潮汐要素的变化Tab. 2 Variation of the K1 tide at different values of E

对于C值, 以 5×10–4为间隔从 0 m 到 6×10–3m取值,K取为 2×10–3,E取为 1×102m2/s。分析发现, 当C取 1×10–3～2×10–3m 时, 计算结果与实测结果符合较好。当C为1×10–3m时计算和实测潮汐调和常数的比较结果见表3, 其中ΔH和Δg分别代表计算和实测分潮的振幅和迟角的差值, 并由此计算出K1和M2分潮振幅和迟角的绝对平均误差, 其中K1分潮振幅的绝对平均误差为 5.4 cm, 迟角的绝对平均误差为5.4°, M2分潮振幅的绝对平均误差为3.5 cm, 迟角的绝对平均误差为7.5°。

3 潮汐潮流的基本特征

3.1 潮汐

图3给出的是K1分潮计算所得同潮图, 其中实线表示迟角, 虚线表示振幅。由图3清晰可见, 在北部湾存在一个退化了的无潮点, 位于 107°5′E,16°40′N。在潮波由南向北的传播过程中, 振幅不断增加, 至北部湾湾顶振幅增至80 cm左右。

图4给出的是M2分潮计算所得同潮图, 其中实线表示迟角, 虚线表示振幅。由图4可见, 北部湾M2分潮的振幅要比全日分潮小得多, 但作为前进波,M2分潮明显地由湾口沿湾轴向湾顶传播, 迟角不断增大。在北部湾西北部的沿岸海域存在一个退化了的无潮点, 这与孙洪亮等[2]计算结果基本一致。

表3 潮汐调和常数计算值与实测值比较Tab. 3 Comparison between the simulated and observed constituent constants

图3 K1 分潮同潮图Fig. 3 Cotidal chart of K1 constituent

图4 M2 分潮同潮图Fig. 4 Cotidal chart of M2 constituent

3.2 潮流

同北部湾的潮汐现象一样, K1分潮潮流占主导地位, K1分潮的最强流速区出现在琼州海峡与海南岛西侧, 最大达70 cm/s。M2分潮的最强流速区则出现在琼州海峡与海南岛西北侧, 最大达20 cm/s左右。无论 K1还是 M2分潮, 它们的潮流长轴方向都与湾轴方向基本一致, 在琼州海峡则呈东西向分布。图5、图6分别列出了北部湾 K1与M2分潮流表层的椭圆长短轴分布, 其中箭头表示流速大小。从图5, 6上可见, 在北部湾大部分海区无论 K1分潮还是M2分潮, 潮流基本呈往复式。除在琼州海峡西侧, K1和M2分潮流表现出很强的旋转性外, K1分潮流在海南岛的西侧也表现出较强的旋转性。

图5 K1分潮表层潮流椭圆分布Fig. 5 Distribution of K1 tidel current ellipses in the surface layer

图6 M2分潮表层潮流椭圆分布Fig. 6 Distribution of M2 tidel current ellipses in the surface layer

3.3 潮余流

由于在北部湾中, K1分潮流占主导地位, 所以作者考虑K1分潮余流。图7给出了K1分潮余流的分布,由图7可见, 琼州海峡的潮余流由东向西, 进入北部湾后向西北而后向西南, 琼州海峡的潮余流最大,约为15 cm/s; 海南岛西岸有一由南向北的沿岸潮余流, 在 19°N附近与折向西南的潮余流汇合, 流速约10 cm/s。这也与孙洪亮等[2]计算结果基本一致。

图7 表层潮余流分布Fig. 7 Distribution of tidel residual current in the surface layer

3.4 水平速度的垂向分布

在北部湾中选取H, G两个点(点位置见图1), 水深分别为60 m和24.9 m。图8给出了H, G点水平速度的垂向分布特征, 垂向采用σ坐标, 水深范围规范化为 0～1, 其中最大流速表层至底层基本一致,反映了潮流是正压流动的特点; 最大流速方向随深度稍微左偏; 海底附近流速变小, 反映了底摩擦的影响。最大流速发生时刻从表层到底层H, G两点分别提前0.1 h和0.2 h。

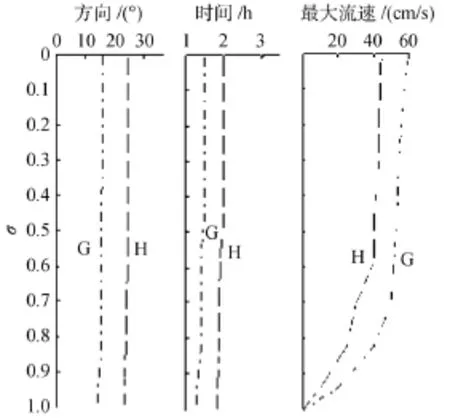
图8 水平速度垂向分布Fig. 8 Vertical distribution of the horizontal velocity

3.5 湍流黏滞系数的垂直分布

由湍能封闭模型得到的垂直黏滞系数同时具有时间和空间的变化, 图9给出了 H点湍流黏滞系数的垂直分布在1～6 h内的变化, 可以看出垂直分布为海底、海面小、中间大的抛物型, 最大值约在深度的中间偏下取得。

4 结论

利用 ECOMSED三维水动力模式, 采用正交曲线坐标, 较好地拟合地形, 对北部湾的潮汐、潮流和潮余流等特征进行了分析, 可以得到以下结论：(1)当海底摩擦系数、水平湍流摩擦系数、海底粗糙度系数分别取 2×10–3, 1×102m2/s, 1×10–3m 时, 计算结果与验潮站观测拟合较好, 其中 K1和 M2两个分潮的绝对平均误差：振幅分别为5.4 cm, 3.5 cm; 迟角分别为 5.4°, 7.5°。(2)在 107°5′E, 16°40′N 有一个退化了的 K1分潮无潮点, 在西北部沿岸海域存在一个退化了的M2分潮无潮点。(3)琼州海峡的K1分潮余流由东向西, 进入北部湾后向西北而后向西南; 海南岛西岸有一由南向北的沿岸潮余流。(4)最大流速表层至底层基本一致, 海底附近流速变小, 反映了底摩擦的影响, 最大流速的方向自上而下稍向左偏,最大流速发生时刻从表层到底层H, G两点分别提前0.1 h和0.2 h。(5)湍流黏滞系数的垂直分布为海底、海面小、中间大的抛物型, 最大值约在深度的中间偏下取得。

图9 H点垂直黏滞系数在6 h内的变化(每隔1 h)Fig. 9 Variation of the vertical turbulent viscosity in 6 hours at point H (every 1 h)

[1]夏华永, 殷忠斌, 郭芝兰, 等. 北部湾三维潮流数值模拟[J]. 海洋学报, 1997, 19(2)：21-31.

[2]孙洪亮, 黄卫民. 北部湾潮汐潮流的三维数值模拟[J]. 海洋学报, 2001, 23(2)：1-8.

[3]殷忠斌, 陈明剑, 李树华, 等. 北部湾潮汐数值计算参数的试验[J]. 广西科学, 1996, 3(2)：71-74.

[4]Blumberg A F. A primer for Ecomsed[M]. America：Hydroqual, Inc, 2002. 1-188.

[5]Chen Changsheng, Beardsley R, Franks P J S. A 3-D prognostic numerical model study of the Georges Bank ecosystem. Part I：physical model[J]. Deep Sea Research Part II: Topical Studies in Oceanography,2001, 48(1-3)：419-456.

[6]Ezer T, Mellor G L. Sensitivity studies with the North Atlantic sigma coordinate Princeton Ocean Model[J].Dynamics of Atmospheres and Oceans, 2000, 32(3-4)：185-208.

Numerical simulation of the tide and tidal current in Beibu Bay

XU Zhen-hua1, LEI Fang-hui2, LOU An-gang3,4, CAO Sheng-shan1
(1. Department of Mathematics, Ocean University of China, Qingdao 266100, China; 2. China Offshore Oil Research Center, Beijing 100027, China; 3. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China; 4. Key Laboratory of Marine Environmental Science and Ecology, Ocean University of China, Qingdao 266003, China)

Mar. , 6, 2006

Beibu Bay; tide; tidal current; numerical simulation

The model ECOMSED with the orthogonal curvilinear grid system is applied to simulating the tide and tidal current in Beibu Bay. We use different coefficients such as bottom friction, bottom roughness and horizontal turbulent friction for the numerical test. The results show that, when coefficient of bottom friction is 0.002 to 0.003,coefficient of bottom roughness is 1×10–3to 2×10–3m and coefficient of horizontal turbulent friction is 1×102to 5×103m2/s, the simulations of the tide and tidal currents agree generally with the observation. The characteristics of the tide, tidal current, and residual current in Beibu Bay are investigated based on the simulation. The vertical turbulent coefficients were found to display a parabolic structure. This study offers more understanding about the hydrodynamic condition in Beibu Bay and provides a scientific basis for the program of environmental protection.

P731.2 文献标识码：A 文章编号：1000-3096(2010)02-0010-05

2006-03-06;

2008-09-09

国家自然科学基金资助项目(40376034)

徐振华(1980-), 男, 山东青岛人, 硕士, 主要从事海洋环境数值模拟研究, 电话：0532-87452228, E-mail：xuzhh@2008.sina.com

刘珊珊)