QR码图像预处理技术研究

陈 杰

(温州大学物理与电子信息工程学院，浙江温州 325035)

QR码图像预处理技术研究

陈 杰

(温州大学物理与电子信息工程学院，浙江温州 325035)

针对光照不均条件下基于图像模式采集到的QR（Quick Response）码图像存在背景比较复杂的情况，提出基于背景灰度扩展的二值化处理方法.对于QR码识别过程中的几何失真，首先通过边界扫描找到畸变矫正控制点，再进行双线性变换矫正失真的条码图像，最后根据探测图形对图像进行旋转矫正.实验表明，方法简单有效，可提高QR码的识别率.

QR码；二值化；几何失真矫正

随着信息技术的发展，二维条码技术在我国的应用越来越广.QR码是二维条码的一种，具有信息量大、可靠性高、超高速全方位识读、高效汉字表示等优点.QR码呈正方形，由名义上的正方形小模块构成，由编码区域和包括寻像图形、分隔符、定位图形和校正图形在内的功能图形组成，结构如图1所示.

图1 QR码符号的结构Fig 1 Structure of QR Codes’ Symbols

二维条码的识读器主要分为两类，一类是激光读取式，一类是图像读取式.激光读取式因为受限于条码的制式，其发展空间变得越来越小.图像读取式因其二维信号的获取优势和可脱离专用识读器的特点，具有很大的发展空间.

目前主要采用以下算法对二维条码图像进行预处理：首先将灰度图像二值化，采用适当的边缘提取算子提取边缘，接着利用Hough变换或投影变换计算二维条码倾斜的角度，最后用双线性变换插值，防止失真[1].使用通用设备采集的条码图像，很容易受到光照不均和采集装置位置导致的几何失真影响，这会给译码带来很大困难，使译码的准确率大大降低.因此，如何对图像进行正确的二值化和几何矫正已成为QR码图像处理要解决的核心问题.

本文针对光照不均条件下的QR码，提出了一种基于背景灰度扩展的QR码图像二值化处理方法.针对QR码图像的几何失真，提出了通过边界点扫描确定几何校正控制点的方法.实验证明，本文的方法可以有效地提高QR码的识别率.

1 QR码图像二值化

与Ostu二值化算法[2]不同，本文提出的基于背景灰度扩展的二值化方法，是通过取适当的阈值使被阈值分开的两组的方差的加权和达到最小，这样容易将QR码中的弱目标合并到背景中去.文献[3]中自适应亮度均衡化采用逐行扫描，这样虽然能达到比较好的效果，但容易引起失真，不能取得满意的结果.本文提出的算法首先对图像的背景亮度进行分块，采取统计的方法，计算该区域中像素亮度的均值和标准差，然后根据统计值进行背景灰度计算，这样有利于排除噪声点的干扰，使鲁棒性更强.处理的具体步骤如图2所示.

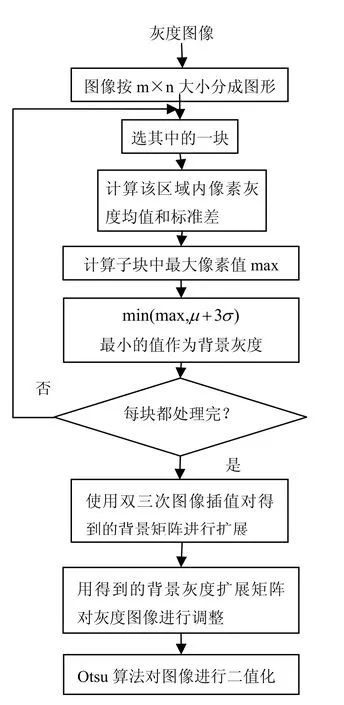
图2 系统流程图Fig 2 Flow Diagram of System

1.1 估计图像背景的灰度

选取图像中适当大小的图形块，计算该区域内的像素灰度均值μ和标准差σ，以 min(max,μ+3σ)作为该区域的背景灰度，其中 max为该区域像素的最大灰度值.

1.2 对背景灰度矩阵进行扩展

根据得到的背景灰度矩阵，将背景灰度矩阵扩展成和原始图像大小相同的矩阵，从而得到背景灰度扩展矩阵.

本文采用双三次图像插值[4]，先对得到的背景灰度矩阵，以行为单位，每4点为插值点进行三次插值，再以列为单位，每4点为插值点进行三次插值.将经过双三次插值后得到的插值图像矩阵作为原背景灰度矩阵的重建矩阵.例如，对128 × 128的图像矩阵A，选取8 × 8大小的图形块计算得背景灰度矩阵B：

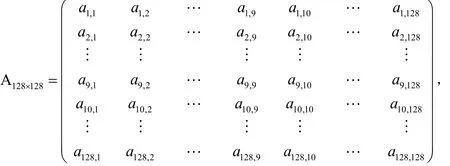
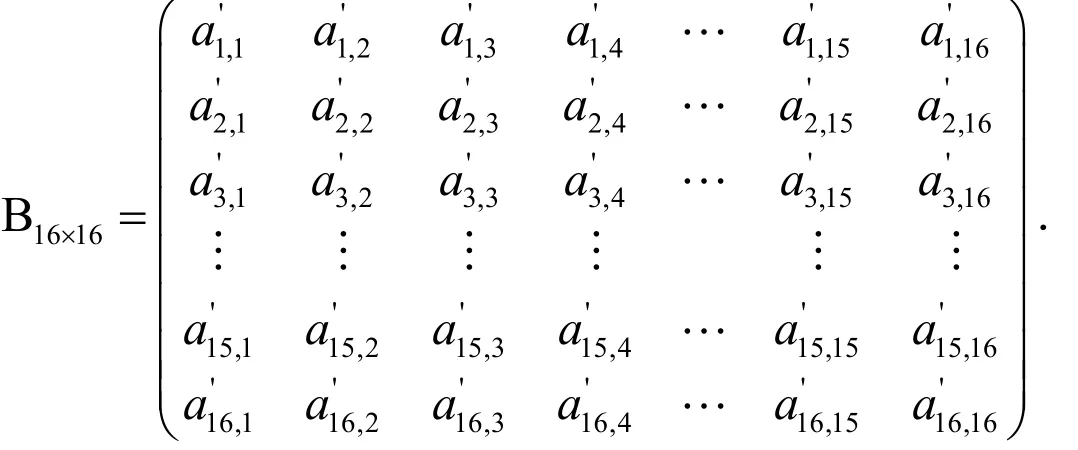
对背景灰度矩阵 B 的第一行进行每4点的三次插值.先以该行的前4个值作为f(x)在背景灰度扩展矩阵C中x=1,10,19,28的函数值，即以(),(),(1 9), (28,)为4个插值点代入下面的插值公式：

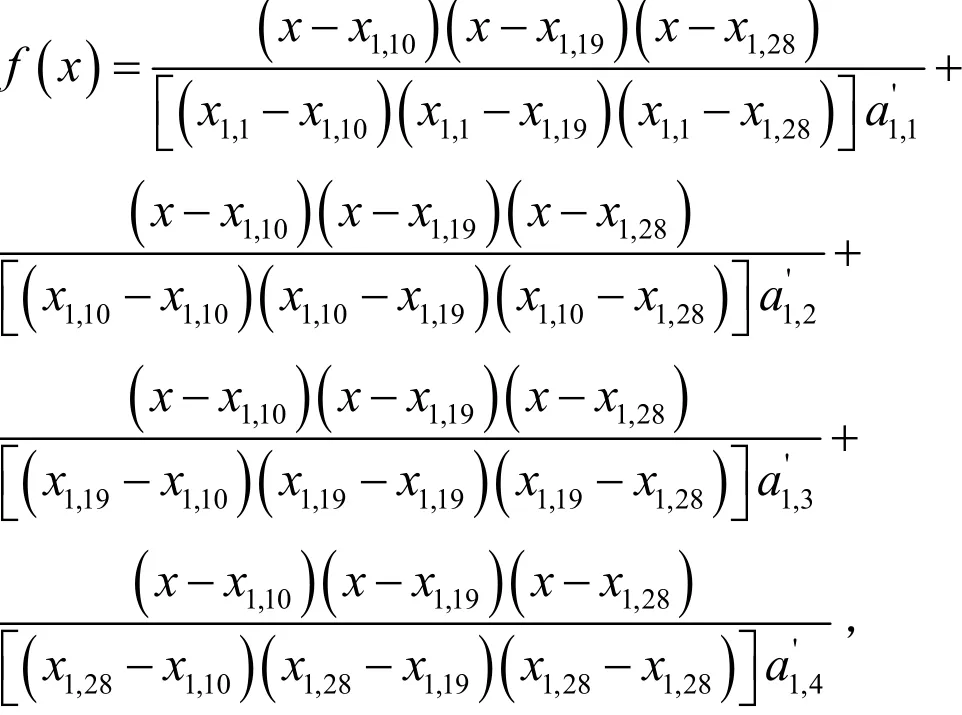
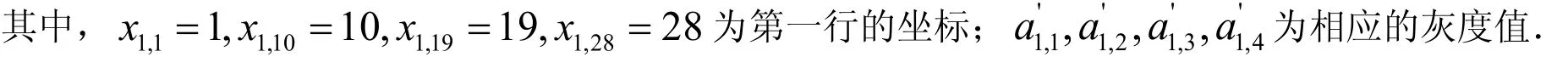
利用上面的插值公式可得a1,1,a1,10和a1,10,a1,19及a1,19,a1,28之间任一点的背景灰度值，即将求得的x=2,3,L,9,11,12,L,18,20,21,L,27的相应的f(x)函数值分别作为a1,x的近似.然后再以为插值点进行类似的三次插值，直到完成第一行的三次插值为止.其它各行均照此处理，完成行的三次插值.用同样方法完成各列的每4个点的三次插值.经过这样的行和列的双三次插值，可得到其它像素的灰度值，从而得到矩阵 B 经扩展后重建的背景灰度矩阵 C.

1.3 原始图像各像素的亮度值调整

用得到的背景灰度扩展矩阵 C调整原始图像各像素的亮度值，使得图像亮度高的区域衰减，亮度低的区域增强.

1.4 对图像进行二值化

对采集的图像分别用Otsu算法、自适应亮度均衡化算法和本文的背景灰度扩展二值化算法进行处理，处理结果如图3所示.

从图3可以看出，对不均匀光照条件下的QR码图像，采用Otsu算法处理容易将弱目标合并到背景中去；采用自适应亮度均衡化算法，虽然能达到比较好的效果，却容易引起失真；本文的背景灰度扩展二值化算法的处理效果最好.

图3 QR码二值化Fig 3 Binarization for QR Codes

2 QR码图像几何失真校正

受图像采集装置中图像传感器平面与条码平面之间的距离、相对角度和两平面的倾角的影响，条码图像往往会发生几何形变.传统寻找控制点的做法是，首先找到3个寻像图形，然后根据寻像图形找到4条边界，从而获得4个控制点.但是当几何失真比较严重，即探测图形模块序列相对比例严重偏离1∶1∶3∶1∶1时，采用传统算法是无法检测到位置探测图形的.对以上情况，可以首先通过边界扫描找到畸变矫正控制点，再进行双线性变换矫正失真的条码图像，最后根据探测图形对图像进行旋转矫正.

2.1 控制点选取

考虑到QR 码的自身特点，本文采用扫描边缘点拟合直线的方法来选取QR码4个顶点，以得到的4个顶点为控制点矫正图像.以图4为例，对算法的具体步骤进行说明.

1）图4（a）为畸变QR码图，对其进行多次灰度腐蚀和膨胀运算，目的是消除条码黑白模块之间的灰度差，最终得到如图4（b）所示的结果.腐蚀运算的结果表现为目标图像的边界点被去除，可以把小于结构元素的物体去除，或者去掉两个物体之间的细小连通.膨胀运算的结果则表现为图像周围的背景点合并到物体中.如果两个物体之间距离比较近，膨胀运算可能会将两个物体连通在一起.

2）对得到的图像即图4（b），利用Canny算子进行边缘检测，可以得到如图4（c）所示的包含条码边缘信息的图像.

3）如图4（d）所示，对所得到的条码边缘图像，从图像中心由内向上进行5次扫描，遇到第一个白点后停止本次扫描，并且记录下白点位置.这样，就可以得到边界上的5个采样点.利用最小二乘法，对这5个采样点进行曲线拟合，可以得到条码的近似边界.同理，从下、左、右三个方向进行扫描可以得到条码的另外三条近似边界.

4）如图4（d）所示，两相邻条码边界的交点即为畸变条码的顶点（4个白色的顶点），这就是我们所要求的4个畸变矫正控制点.

5）根据得到的控制点建立起校正前后图像的映射关系，利用这种映射关系对发生畸变的条码图像进行畸变校正.

2.2 平面投影转换

因为几何失真，得到的4个控制顶点会构成一个四边形，至少需要再进行一次形状上的转换，将四边形转换为正方形才可以让后续解码器识读，如图5所示，A、B、C和D点分别必须对应到条码的左上角（A'）、右上角（B′）、右下角（C′）和左下角（D′）.

套用Perspective Transform[5]平面投影转换公式，将原来的四边形转换为正方形.下面（1）式和（2）式中的(x,y)为原始拍摄影像上QR码坐标，(u,v)为平面投影转换后的正常坐标，a,b,c,d,e,f,g,h为转换公式中待解的8个参数，至少将转换前后4组坐标点对应代入（1）式和（2）式后才可得参数解.

图4 几何变换Fig 4 Geometric Transformation

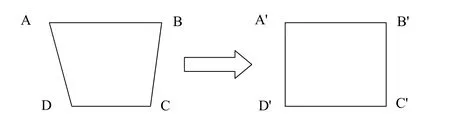
图5 控制点变换原理图Fig 5 Schematic Diagram of Control Point Transformation

整理后可得：

取QR码左上角、右上角、右下角和左下角4点坐标代入（3）式和（4）式后得：

经过条码定位流程取得的QR码4个顶点坐标，透过平面投影转换后，对应到预先设置的形状为正方形的坐标，将转换后正方形的边长设为原先4条边长的平均值W，中心点不变，可得该4点坐标对应点，依次为条码左上角、右上角、右下角和左下角的4个坐标.将各点坐标分别代入（5）式中计算可得：

将解出的8个参数代入（1）式和（2）式，得到 (u,v)坐标点对应到转换前的原始图像上的(x,y)，QR码平面投影转换的结果如图4（f）所示.

2.3 定位与定向

图6（a）为几何失真矫正后的结果，但是可以明显看出QR码并没有旋正，本来应该在左上角的探测图形，这时候在右下角，所以还要通过定位探测图形，来确定QR码的旋转角度，从而达到旋转定向.确定3个位置探测图形后，需要确定条码的方向，此时可以连接3个探测图形的中心点，构成一个三角形.设该三角形的3个角分别为α、β、δ.根据QR码的结构特征可知，3个角中度数最大的角的顶点就是QR码符号左上角的探测图形的中心点.所以只要以此中心点位置为参考，旋转一定角度（90°的整数倍）就可以实现条码符号的定向，如图6（c）所示.

图6 QR码旋转矫正Fig 6 Revolving Correction of QR Codes

2.4 对图像进行几何失真矫正

本文使用通用图像采集装置（照相手机）采集40幅QR码图像，分为普通光照明、弱光照明、强光照明、不均匀光照明几类，采样的分辨率为640 × 480.从QR码的下侧、上侧、右侧、左侧4个方向采集，分别用传统算法和本文的算法确定控制点，对图像进行几何失真矫正，处理结果见表1.图7所表示的为采集到的部分原始图像与其用本文算法进行几何失真矫正后的结果.

图7 QR码图像的几何失真矫正Fig 7 Geometric Distortion Correction of QR Codes’ Images

从表1可以看出，本文提出的通过边界点扫描确定几何矫正控制点的矫正方法，可以有效提高QR码的识别率.

表1 QR码解码结果统计Table 1 QR Code’s Decoding Result

[1]郑河荣, 熊丽荣, 王天舟. 基于HOUGH变换的二维条码图像矫正[J]. 浙江工业大学报, 2003, 31(2): 169-172.

[2]Otsu N.A threshold selection method from gray-level histo-grams [J]. IEEE Transactions Oil Systems, Man and Cybernetics, 1979, 9(1): 62-66.

[3]Hsia S C, Chen M H, Chen Y M. A cost-effective line-based light-balancing technique using adaptive processing [J]. IEEE Transactions on Image Processing, 2006, 19(5): 2719-2729.

[4]Durand C X, Faguy D. Rational zoom of bit maps using B-spline interpolation in computerized 2-D animation [J]. Computer Graphics Forum, 1990, 9(1): 27-37.

[5]Bleyl R L. Using Photographs to Map Traffic Accident Scenes: A Mathematical Technique [J]. Journal of Safety Research, 1976, 1: 59-64.

Research on Technique of QR Code Images Preprocessing

CHEN Jie
(College of Physics and Electronic Information Engineering, Wenzhou University, Wenzhou, China 325035)

Due to the ununiform lighting condition, the light background of QR (Quick Response) codes’images captured on the basis of image pattern might be complicated. Based on this phenomenon, a binary processing method, which is based on background gray-scale extension, was proposed. In the correction process of geometric distortion happened in recognition of QR codes’ images, control point of distortion correction should be identified by boundary scan in the first stage; distorted QR codes’ images should be corrected by means of bilinear transformation in the second stage; and the obtained images should be corrected by revolving the images at last. Experimental results showed that the method, which is simple and effective, can be used to improve precision of QR codes’ recognition rate.

QR Code; Binarization; Correction of Geometric Distortion

(编辑：王一芳)

TP391.41

A

1674-3563(2010)06-0016-08

10.3875/j.issn.1674-3563.2010.06.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2010-03-30

陈杰(1983- )，男，浙江宁海人，硕士研究生，研究方向：嵌入式图像处理