应用克兰克-尼克尔森法求解对称势阱中的 BECs波函数

杜 磊

(山西大学物理电子工程学院,山西太原 030006)

应用克兰克-尼克尔森法求解对称势阱中的 BECs波函数

杜 磊

(山西大学物理电子工程学院,山西太原 030006)

通过相互作用玻色子的二次量子化哈密顿量得出 G-P方程,说明计算双阱中 BECs波函数的重要性,最后应用克兰克-尼克尔森法数值计算得出任意一维对称双阱中左右阱的BECs的波函数.

克兰克-尼克尔森法;G-P方程;对称双阱;动力学方程

0 引言

近年来,处于两空间分离的弱耦合玻色-爱因斯坦凝聚体 (BECs)之间的宏观量子特性成为研究热点.对于两空间分离的弱耦合 BECs,囚禁其双势阱对该凝聚体的动力学性质有很大的影响,在不同的双势阱中BECs的动力学特性会有很大的差异,该特点对我们研究BECs将会有极大的帮助.同时,理论与实验对各种双势阱中 BECs动力学性质的研究也是近年来 BEC领域中的热点之一[1-3].

在研究不同的双势阱中BECs动力学性质时,很重要的一点是必须得到左右两个阱中的凝聚体波函数.一般情况下,该波函数需用数值方法才能计算出来,特别是当势阱形状要任意改变时.本文主要介绍了一套数值方法以研究对称势阱中BECs的波函数.

1 对称势阱中弱耦合玻色-爱因斯坦凝聚体的动力学方程

其中,^ψ+(r)和^ψ(r)分别是在r点玻色子场的湮灭和产生算符,U(r-r′)是两个玻色子间的相互作用势.

当弱相互作用的玻色气体为非均匀凝聚体时,即在有外场的作用下,使得凝聚体的性质,如临界温度、凝聚粒子数比率以及玻色气体热容量等等,都依赖于囚禁势的形状.此时,玻色子的场算符变为=Ψ(r)+.此处,Ψ(r)=＞,即Ψ(r)是玻色子场算符在系综水平上的统计平均值,通常称之为凝聚体的波函数.而是非凝聚体各态的场算符,一般在凝聚体的耗散很小时它是一个小量,满足＜＞=0.在稀化的玻色气体中,原子间的相互作用一般都较弱,所以我们可以使用一个简单的近似来简化原子间的相互作用势:其中m是玻色子的质量,a为s波散射长度,用δ(r)表征玻色子之间的相互作用是接触碰撞相互作用.将玻色子的场算符和相互作用玻色子的二次量子化的 Hamilton量式代入到海森堡方程,并将简化后的原子间的相互作用势代入,定义并在计算过程中考虑玻色-爱因斯坦凝聚体的特性[5],得:此即 G-P方程.

考虑置于对称势阱中的BECs[6-8],其波函数形式可通过求解含时 G-P方程(2)得到,我们寻找如下形式的解:

2 克兰克-尼克尔森法

由 John Crank和 Phyllis Nicholson发明的隐式差分格式[9]是基于求解网格中在行之间的点(x,t+k/2)处的抛物型方程

根据初始条件及边界条件,式(11)中右边的项都是已知的,因此可以将其化为三角形线性方程组 AX=B的形式,这样我们就可以通过迭代的方法求得(7)的数值解.

3 对称双阱中波函数的数值求解

对 G-P方程(2),考虑一维情况,并将其无量纲化和引入虚时间τ=it,可简化为[10]:

其中Vext为有效势,g1d描述玻色子间的相互作用强度.

由(4)我们知道,对称势阱中的玻色-爱因斯坦凝聚体,其基态及激发态波函数对应Φ+和Φ-,且Φ+、Φ-分别具有对称性和反对称性.因此若初始的试探波函数为偶函数,则可以通过上述方法求得Φ+,反之试探波函数取奇函数可求得Φ-.这样通过式(14)就可求得局域于势阱i(i=1,2)的波函数Φi(r).

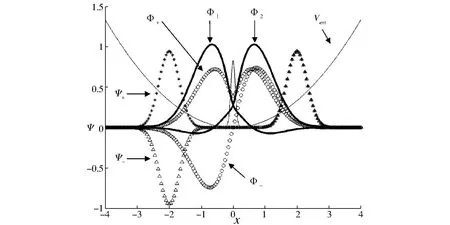
图 1 对称势阱中 BECs波函数Fig.1 W ave Function of BECs in 1D Symmetry Trap

总之,我们从最基本的相互作用玻色子二次量子化哈密顿量出发得出 G-P方程,再通过推导了两空间分离弱耦合 BECs动力学方程说明了计算双阱中 BECs波函数的重要性,最后介绍了应用克兰克-尼克尔森方法通过数值计算得出任意对称双阱左右阱中 BECs的波函数.这一套完整的方法可以用来研究任意对称势阱中BECs的波函数及其动力学性质,大量工作表明不同的对称势阱对其中 BECs动力学特性影响非常大,该特点为我们加深对BECs的认识会提供极大的帮助.

[1] GIOVANAZZIS,SM ERZIA.FANTON IS.Josephson Effects in Dilute Bose-Einstein Condensates[J].Phys Rev Lett,2000,84:4521-4524.

[2] ALB IEZ,M.Direct Observation of Tunneling and Non linear Self-trapping in a Single Bosonic Josephson junction[J].Phys Rev Lett,2005,95.

[3] LEVY S,LAHOUD E,SHOMRON I1 I,et a l.The a.c.and d.c.Josephson Effects in a Bose-Einstein Condensate[J].Nature,2007,449:579.

[4] DALFOVO F,GIORGIN IS,PITAEVSK IIL P,eta l.Theory of Bose-Einstein Condensation in Trapped Gases[J].Rev Mod Phys,1999,71:463.

[5] 李秀平,刘文森,张国锋.外势场中玻色-爱因斯坦凝聚性质的研究[J].量子光学学报,2003(1):27-31.

[6] JUHA JAVANA INEN.Non linearity from Quantum Mechanics:Dynamically Unstable Bose-Einstein Condensate in a Double-well trap[J].Phys Rev A,2010,81,051602(R).

[7] RAGHAVAN S,SM ERZIA,FANTON IS,eta l.Coherent Oscillations Between Two Weakly Coupled Bose-Einstein Condensates:Josephson effects,π oscillations,and macroscopic quantum self-trapping[J].Phys Rev A,1999,59:620-633.

[8] ZHANG Yun-bo,Müller-Kirsten H JW.Instanton App roach to Josephson Tunneling Between Trapped Condensates[J].Euro Phys JD,2001,17:351-363.

[9] JOHN H.MATHEW S,KURTISD FINK.数值方法 (MATLAB版)[M].周璐等译,北京:电子工业出版社,2005,12:432-435.

[10] HAO Ya-jiang,LIANG J-Q,ZHANG Yun-bo.Numerical Simulation on Tunnel Splitting of Bose-Einstein Condensate in Multi well Potentials[J].Euro Phys JD,2005,36:33.

Apply Crack-Nicholson Method to Resolve GP Equation and Get the Wave function of Bose Einstein Condensates in Symmetry Trap

DU Lei
(School College of Physics and Electronic Engineering Shanxi University,Taiyuan030006,China)

We use the Hamiltonian of the quadratic quantization between the interacting bosons to obtain the G-P equation,based on which the new dynamic equation about two weak coup ling BECs(Bose Einstein Condensates)with space separated is derived.Moreover,we calculate the wave functions of the left and right well respective in arbitrary 1D symmetric dual wells with C rack-Nicholson method.

Crack-Nicholson Method;G-P Equation;symmetry dual trap;dynamics equation

文章编号：0253-2395(2010)04-0577-05

O469

A

0253-2395(2010)04-0547-04

2010-04-28;

2010-07-11

山西省研究生优秀创新项目 (20093004)

杜 磊 (1981-),男,山西娄烦人,讲师,在读博士,主要从事凝聚态物理研究.E-m ail:dulei@sxu.edu.cn

book=550,ebook=122