XCP投弃式海洋探头阻力系数数值计算及试验研究

刘 宁 ，张 瑞 ，陈文义，张曼曼 ，陶金亮

（1.国家海洋技术中心，天津 300112;2.河北工业大学 化工过程机械专业，天津 300130）

XCP投弃式海洋探头阻力系数数值计算及试验研究

刘 宁1，张 瑞2，陈文义2，张曼曼2，陶金亮2

（1.国家海洋技术中心，天津 300112;2.河北工业大学 化工过程机械专业，天津 300130）

以XCP探头为模型，采用有限体积法结合κ-ε两方程湍流模型，对XCP探头阻力系数进行了数值计算，研究了XCP探头的阻力特性。获得了不同雷诺数下阻力系数的变化趋势和水下稳定运动时的极限速度。结果表明阻力系数随着雷诺数的增加而减小，其数值计算结果与海上实测数据基本吻合，验证了该数值计算方法的正确性，可为XCP探头结构设计提供参考。

阻力系数；极限速度；数值计算；XCP探头

引言

XCP投弃式海洋探头，可快速获取海洋环境剖面参数，主要用于科学调查、海洋环境预报、海洋环境监测和海军舰船的机动海洋动力环境观测等方面。目前掌握该类技术并生产这类仪器的国家只有美国和日本，为了打破国外对该技术的垄断，21世纪初我国开始对船载XCP投弃式剖面测量技术进行研究。

XCP探头的阻力系数是一个重要参数，它用于对探头进行优化设计，并为海上试验提供理论参考；通过阻力系数可根据公式[1]进一步算出探头入水极限速度，进而预测探头入水深度，为获得入水深度随时间的变化曲线提供保障。探头阻力与外形，尾翼翼型，表面积等多方面有关[2]。目前阻力系数可以通过水洞试验、探头海上实际投放和流场测量分析得到[3]。前两种方法所需费用较高，且测量结果依赖于试验手段，存在较大不确定性；第三种方法需要对流场进行复杂繁衍计算，工作量大。通过数值计算的手段进行探头阻力系数的研究，可以节约大量时间和经费。本文针对XCP探头进行阻力系数和入水极限速度的研究，并用国家海洋技术中心获得的海上试验数据进行验证，确保数值计算结果的科学性和合理性。研究结果对XCP探头水下运动规律研究和探头的设计具有参考价值。

1 数值计算基本假设

试验采用国家海洋技术中心设计的XCP探头模型，探头重1.65 kg，最大截面直径51 mm。图1为根据实物建立的XCP探头计算模型。为简化计算，忽略内部复杂结构；不考虑线圈释放时对阻力系数的影响；XCP探头以速度0 m/s从海平面开始垂直下落[4]。

图1 XCP探头计算模型

2 XCP探头运动基本方程

由于探头是轴对称体，且计算中只考虑垂向运动。建立坐标系如图2所示，

图2 求解坐标系

探头下落运动的运动方程和动量方程如下[5]：

式中：M为探头质量；m为附加质量（附加质量在探头做变速运动时是一个常数）；z为探头下落位移；v为探头下落速度；Ff为探头所受浮力；D为探头所受阻力；z0为探头初始位移；v0为探头初始速度。

海水浮力的计算：

式中：ρf为海水密度；Vt为探头的体积；G为重力加速度。

海水阻力计算：

探头在海水中下落阻力计算公式为：

式中：Cd为总阻力系数；S为物体浸湿投影面积；v为探头水中运动速度。

雷诺数计算：

探头周围的海水处于湍动状态，以XCP探头最大横截面直径Dmax和均匀来流速度v'为特征长度和特征速度，v为运动学粘性系数。则雷诺数可表示为：

3 控制方程与数值计算方法

计算流场设为黏性、不可压缩非稳态流场，采用k-ε两方程湍流模型。方程组如下[6]：

计算模型的求解采用有限体积法。设置探头与海上实验相同的16 r/s转速旋转。方程采用SIMPLE[7]算法进行压力和速度的耦合求解，对流项的离散采用二阶迎风格式[8]。计算域外边界包括模型表面设定为无滑移的壁面。计算域的入口设为速度入口，出口设为outflow。

4 模拟结果与实验结果比较分析

通过对不同雷诺数下XCP探头的数值计算，得出阻力系数变化规律。试验数据来自于国家海洋技术中心2009年10月在南海进行的运动测试试验。试验通过XCP探头传感器和接收设备，记录探头下沉全过程中获得的参数。根据探头下落的位移与时间关系，可以得出加速度以及阻力的大小，进而得出了不同雷诺数下的阻力系数。图3为数值计算与试验得到的雷诺数与阻力系数关系图。由图3可以看出，数值计算结果与试验结果基本吻合，阻力系数随着雷诺数的增加而减小。模拟结果小于试验结果的原因可能是模拟时建立的计算模型光滑，造成了摩擦阻力的减小，同时没有考虑探头释放导线造成的探头总质量和排水体积的变化及海水密度变化等复杂环境因素对阻力系数的影响。

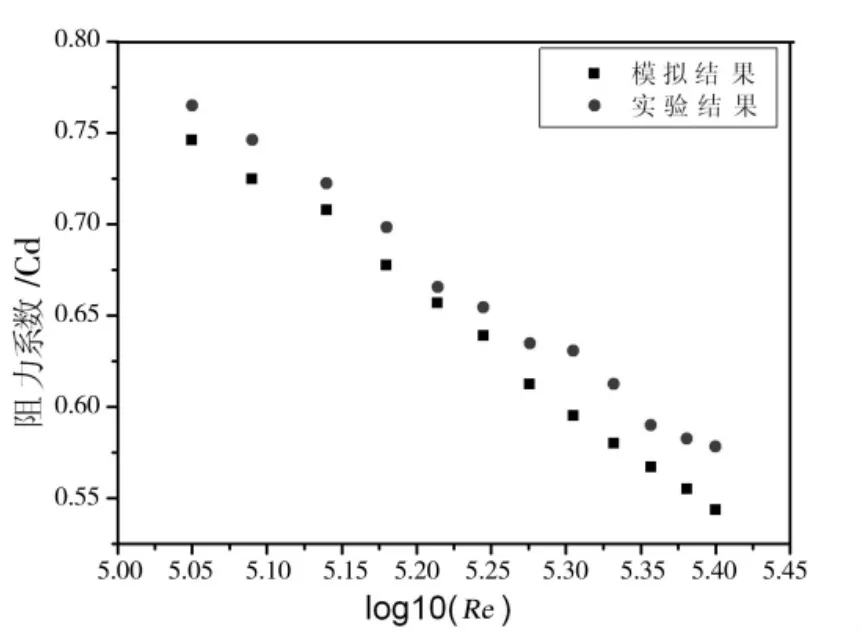
图3 阻力系数与雷诺数关系

从公式⑶可以看出，探头下降至阻力D=Mg-Ff时，将达到极限速度，之后物体将以此极限速度VT下降。位移与时间变化实测曲线，XCP探头阻力拟合比较图分别如图4、图5所示。

图4中位移和时间成线性变化，对图4国家海洋技术中心提供的XCP探头海上实验位移与时间实测曲线进行微分，获得了探头极限下落速度为3.799 2 m/s。图5通过数值计算获得的阻力系数，得到不同速度下阻力散点分布，根据散点分布拟合出阻力拟合曲线。由图5可知当阻力D=Mg-Ff时，极限速度为4.062 1 m/s。

图4 位移与时间变化实测曲线

图5 XCP探头阻力拟合比较图

表1 试验结果与模拟结果对比

表1为试验结果与数值计算结果关系。通过表1可以看出，数值计算结果与实验结果基本吻合，误差控制在10%左右，验证了数值计算模型的正确性和可行性。

5 结论

本文通过对XCP探头阻力系数数值计算的研究，得出主要结论如下：

（1）通过数值模拟得到了XCP探头的阻力系数和极限速度，阻力系数及极限速度随着雷诺数的增加而减小。并经国家海洋技术中心海域实测试验结果验证，吻合性较好，证明了数值计算方法的可行性。

（2）计算中对探头XCP阻力系数的确定具有一定的代表性，该数值计算方法可为其它类型探头的研究提供借鉴。

通过对不同雷诺数下阻力系数的对比分析，为探头结构的优化设计提供技术保障；同时对阻力系数变化规律的分析，还可以为进一步模拟其它因素对XCP探头的影响提供观察指标。

[1]孙涛，黄银水，陶建华.抛弃式温盐探头运动状态的数值模拟及其实验验证[J].海洋通报，2002，21(2):70-71.

[2]赵志敏，冯会全,冯旭.导弹水中阻力特性分析[J].战术导弹技术,2009(1):17-20.

[3]黄银水,陶建华.线圈释放式温、盐、深探头运动特性的数值计算方法研究[J].海洋技术,2003(3):45-48.

[4]刘宁.国家高技术研究发展计划（863计划）项目.2006.

[5]肖鸿,刘长根,陶建华.抛弃式温盐探头阻力系数的数值模拟及其实验验证[J].海洋技术,2006(3):35-37.

[6]童秉纲.鱼类波状游动的推荐机制[J].力学与实践,2000,22(3):69-74.

[7]B E Launder,D B Spalding.The Numerical Computation of Turbulent Flows[J].Computer Methods in Applied Mechanics and Engineering，1974,3:269-289.

[8]于勇.FLUENT入门与进阶教程[M].北京:北京理工大学出版社,2008.

A Numerical Study on Drag Coefficient of XCP Probe

LIU Ning1,ZHANG Rui2,CHEN Wen-yi2,ZHANG Man-man2,TAO Jin-liang2
（1.National Ocean Technology Center,Tianjin 300112,China;2.Hebei University of Technology,Chemical Process Mechanics Department,Tianjin 300130）

In order to study the drag coefficient of XCP probe,through the analysis of the basic equations of motion,the drag coefficient of XCP probe model was numerically simulated by finite volume methods.The drag coefficient under different Reynolds number and the limited velocity under submarine steady motion were obtained.The simulated results showed that the drag coefficient decreased as the increase of Reynolds number,which is approximately accordant to the experimental results.Compared with the experimental results,the numerical analysis method was justified.These research results will provide theory reference for the optimization design of XCP probe.

drag coefficient;limited velocity;numerical calculation;XCP probe

P716

A

1003-2029（2010）04-0012-03

2010-08-02

国家高技术研究发展计划（863）资助项目(2006AA09A304)；河北省自然科学基金资助项目（D2009000035）

刘宁（1977-），男，博士，主要研究领域：信号处理、海洋监测。Email:liun0130@yahoo.com.cn