L HS抽样遗传算法
2010-01-06陈明华
任 哲,陈明华
(1.合肥学院数理系,安徽合肥230022;2.皖西学院数理系,安徽六安 237012)
L HS抽样遗传算法
任 哲1,陈明华2
(1.合肥学院数理系,安徽合肥230022;2.皖西学院数理系,安徽六安 237012)
文献[1]研究了遗传算法的运行机理及特点,即遗传算法是一个具有定向制导的随机搜索技术,其定向制导的原则是:导向以高适应度模式为祖先的“家族”方向。以此结论为基础,利用拉丁超立方体抽样(LHS)的理论和方法,对遗传算法中的交叉操作进行了重新设计,给出了一个新的GA算法,称之为LHS遗传算法。将L HS遗传算法应用于求解优化问题,并与简单遗传算法和文献[2]中的佳点集遗传算法进行比较,通过模拟比较,可以看出新的算法不但提高了算法的收敛速度和精度,而且避免了其它方法常有的早期收敛的现象。
遗传算法(GA);拉丁超立方体抽样(LHS);LHS遗传算法(LHSGA)
1 引言
文献[1]指出了GA算法的本质是:遗传算法是一个具有定向制导的随机搜索技术,其定向制导的原则是:导向以高适应度模式为祖先的“家族”方向。文献[2]根据此机理,利用数论中的佳点集理论和方法[3]设计了一个新的交叉算法,提高了GA算法的效率。简单介绍文献[2]中给出的佳点集遗传算法。
1.1 佳点集GA算法
设在传统的GA算法基础上,在进行过复制后,对池中的元素按赌轮法选择两个元素A1,A2进行佳点集交叉操作。

不妨设A1,A2的前t个分量不同,后l-t个分量相同,令模式

由A1,A2进行交叉(不管是单点交叉或是多点交叉)其子孙必属于H,于是要在“高适应度模式为祖先的家族方向”上搜索出更好的样本,就是要在H中搜索出更好的样本。佳点集GA算法就是在H上利用佳点集方法找出好样本来,其方法是[2]:
将H的前t个分量看成一个t维的立方体(仍记为H)然后在H上求佳点集。
在t维空间中取佳点的方法如下:
在t维空间H中作含n个点的佳点集(当H是二进制立方体时)

其中rk=2cos(2πk/p),1≤k≤t,p是满足p≥2t+3的最小素数,或rk=ek,1≤k≤t,{a}表示a的小数部分。令交叉后产生的n个后代中第k个染色体

〈a〉表示,若a的小数部分小于0.5,则〈a〉=0;否则〈a〉=1。
这样在其“家族”中,产生n个后代,取其中适应度值最大者(或最大的几个),作为交叉后的后代。上述交叉操作,称为佳点集交叉操作。

1.2 拉丁超立方体抽样(L HS)
设在一个d—维单位立方体Cd=[0,1]d中要选n个点,先将每一维坐标区间[0,1]都分成n等分,并用标号i记小区间第j维坐标的n个标号(1,2,…,n)的一个随机排列。又设这d个随机排列相互独立,则得到一个n×d阶的随机矩阵π=(πij),然后令



为一个Latin Hypercube样本。我们称这样的抽样方法为L HS。所得到的样本称为L HS的样本。
在某种意义下,L HS是一种分层抽样,就某种均匀性来说要优于i.i.d.抽样(常指Monte Carlo抽样)。而且文献[5]、[6]都说明L HS具有良好的散布均匀性和代表性,加之它是随机的,搜索能力更强,故比佳点集有更好的表现。
2 L HS遗传算法
2.1 L HS交叉操作
设在传统的GA算法基础上,在进行过复制后,对池中的元素按赌轮法选择两个元素A1,A2进行L HS抽样交叉操作。

不妨设A1,A2的前t个分量不同,后l-t个分量相同,令模式
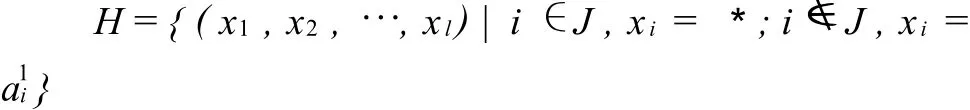
由A1,A2进行交叉(不管是单点交叉或是多点交叉)其子孙必属于H,于是要在“高适应度模式为祖先的家族方向”上搜索出更好的样本,就是要在H中搜索出更好的样本,L HS遗传算法就是要在H上利用L HS方法来找出好样本,其具体方法是[4]:
将H的前t个分量看成一个t维的立方体(仍记为H)然后在H上进行L HS抽样或将H的每d个分量分成一组(不妨设共分成s组),每组表示一个实数。于是s个组就表示s个实数。这样就将H变换成一个s维的实空间,可将其归一化变换成一个s维的单位立方体。然后在其上进行L HS抽样。
如(1,1,0,0,1,0,1,0,1,1,0,1)是12维二进制单位立方体中的一点,我们可以将它化成三维的实值空间的点(每4个分量合成一个实数)(1100,1010,1101)=(12,10,13);再将它归一化,得点(12/16,10/16,13/16)=(3/4,5/8,13/16),即为实3维单位立方体中的一点。
在t维空间中进行L HS的具体做法如下:


〈a〉表示:若a的小数部分小于0.5,则〈a〉=0;否则〈a〉=1。
这样在其“家族”中,产生n个后代,取其中适应度值最大者(或最大的几个),作为交叉后的后代。
上述交叉操作,称为L HS交叉操作。
变异:取染色体A,随机整数i,A=(a1,a2,…, al)变异成新的染色体B,

2.2 L HS遗传算法
给定交叉概率pc和变异概率pm,L HS遗传算法如下:
(1)每次进行遗传操作,以概率fi/∑fi复制A i,其中fi是A i的适应度值。
(2)以赌轮法随机取两个染色体,以概率pc对其进行L HS交叉操作(产生n个后代,n为待定参数)。
(3)以概率pm进行变异遗传操作。
(4)把经过遗传操作后得到的染色体都放到染色体池中,对新得到的染色体,计算其适应度值。若假定染色体的容量一定,当染色体的个体超过容量时,就将适应度小的染色体从池中删去(或按a%进行删除)。
(5)进行上述的遗传算法至第T代后(T是预先给定的常数),在第T代的染色体中取适应度最大的染色体,即为所求的染色体。
3 L HS遗传算法的测试比较和实验分析
在P4 3.0G PC机器上,在Matlab7.0计算平台上,利用遗传算法工具箱中“简单遗传算法”、文献[2]中的“佳点集遗传算法”和这里的“L HS遗传算法”对文献[2]中提供的5个函数进行了计算比较;计算中遗传算法参数为:种群规模为100,最大迭代代数为150,交叉概率为0.85,变异概率取0.05,每个执行100次。


实验结果:
表中:GA:简单遗传算法;GGA:佳点集遗传算法;L HSGA:拉丁超立方抽样遗传算法。
从上面结果可见,不管在求解精度上,还是在求解速度上,基于L HS的遗传算法比传统简单遗传算法和佳点集遗传算法的性能都要好得多,并能成功地避免“早熟”现象。
4 结论
本文改进了遗传算法中的交叉操作,我们知道遗传算法是一个具有定向制导的随机搜索技术,其定向制导的原则是:导向以高适应度模式为祖先的“家族”方向,所以任何一种交叉操作都无非是在以其父代为“祖先”的“家族”中寻找一个适应度值高的后代。现有的交叉算法:如单点交叉、多点交叉、树交叉[8]等,都只能保证求到的后代落在上述的家族中,但其搜索适应度值高的后代的能力不够强;佳点集法利用求得的子集的均匀散布性,使它们能较好代表其“家族”性能的普遍性,所以佳点集遗传算法构造的交叉操作提高了搜索适应度值高的后代的能力,但佳点集布点有方向性,并且当n取定后是确定的,不带随机性,更非统计意义下的抽样,这导致了其整体搜索能力仍不够强。L HS就克服了此不足,L HS所得的样本具有很好的均匀散布性,并且每次取得的样本集是随机均匀散布的,这样可以取到所有的格子点。所以L HS[4]遗传算法具有极强的整体搜索能力。实验证明不管在求解精度上还是在求解速度上,L HS遗传算法不仅优于GA算法,也优于佳点集遗传算法,并能较好地避免早熟现象,收敛到最优解。
[1]张铃,张钹.遗传算法机理的研究[J].软件学报,2000,11 (7):945-952.
[2]张铃,张钹.佳点集遗传算法[J].计算机学报,2001,24 (9):917-922.
[3]华罗庚,王元.数论在近似分析中的应用[M].北京:科学出版社,1978.
[4]Mekay.M.D.,Beckman.R.J.and Conover.W.J.A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Out Put from A Computer Code[J].Technometrics,1979,21:239-245.
[5]Stein.M.Large Sample Properties of Simulations Using Latin Hypercube Sampling[J].Technometrics,1987,29: 143-151.
[6]Owen,A.B.A Central Limit Theorem for Latin Hhypercube Sampling[J].J.R.Statist.Soc.Ser.B,1992,54:541 -551.
[7]吴少岩,张青富,陈火旺.基于家族优生学的进化算法[J].软件学报,1997,8(2):137-144.
[8]陈国良,王煦法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,1996.
Genetic Algorithm Based on Latin Hypercube Sampling
REN Zhe1,CHEN Ming-hua2
(1.Dept.of Mathematics and Physics,Hefei University,Hefei230022,China;2.Dept.of Mathematics and Physics,West Anhui University,L u’an237012,China)
By analyzing the genetic algorithm(GA)based on it’s idea density model,the essence and characteristics of GA are given. It is shown that the GA is a guided random search and the guiding direction always aims at the family whose ancestors have schemata with high fitness.Based on the results,the crossover operation in GA is redesigned by using the principle of Latin Hypercube Sampling.Then a new GA called Genetic Algorithm based on Latin Hypercube Sampling is presented.The new GA is applied to optimization function.Compared to Simple Genetic Algorithm(SGA)and Good Point Genetic Algorithm(GGA)for solving this problem,the simulation results show that the new GA has superiority in speed,accuracy and overcoming premature.
genetic algorithm(GA);Latin hypercube sampling(LHS);genetic algorithm based on Latin hypercube sampling(LHSGA)
TP301
A
1009-9735(2010)02-0018-04
2010-03-31
任哲(1957-),女,安徽淮南人,合肥学院数理系教授,研究方向:参数统计和大样本理论、人工智能、遗传算法。
陈明华(1954-),男,浙江鄞县人,皖西学院数理系教授,研究方向:参数统计和大样本理论、人工智能、遗传算法。
