用神经网络和地质统计学综合多元信息进行储层预测

李东安,宁俊瑞,刘振峰

(1.中国地质大学资源学院,湖北武汉430074; 2.中国石油化工股份有限公司石油勘探开发研究院,北京100083)

用神经网络和地质统计学综合多元信息进行储层预测

李东安1,宁俊瑞2,刘振峰2

(1.中国地质大学资源学院,湖北武汉430074; 2.中国石油化工股份有限公司石油勘探开发研究院,北京100083)

由于实际地下地质地球物理条件的复杂性和地震等资料品质所限,相关问题的解决较为困难。在研究中如何将多元信息结合起来是实现这一目标的可行途径。遵循这一思路,在D气田地震储层预测中,针对研究区储层地质、地球物理特点,尝试用神经网络和地质统计学作为不同信息的融合平台,并将二者结合起来,充分地将多种地震属性和测井资料相结合,有效地减少了储层预测的多解性,提高了储层预测精度,达到了良好的应用效果。

地震属性;神经网络;地质统计学;储层预测

减少预测结果的多解性、提高预测精度是储层地震预测的永恒话题。由于地震储层预测是一个典型的信息不对称问题,充分地占有多元信息对于减少问题的不对称性、减少储层预测的多解性至关重要。量纲不同、机理不同的信息如何充分地融合是业内人员始终关注的问题。目前比较成熟的方法主要有两种:一种是神经网络方法,另一种是地质统计学方法[1～7]。在实际应用中,两种方法及以其为基础的相关软件多单独使用。由于两种方法各有优劣,在面对复杂的储层地质地球物理条件时,单一方法的使用难以取得理想的效果[8～13]。基于以上考虑,笔者在从事大量的地震储层工作基础上,尝试着将神经网络和地质统计学两种数据(信息)融合平台结合起来使用。通过在D气田致密碎屑岩储层预测中的应用实践,证实了这一方案的有效性。

1 方法原理

1.1 概率神经网络属性优化

概率神经网络实际上是用神经网络结构来实现数学内插[10]。通过比较新点处的新属性与已知的培训中的属性来确定每一个点的输出,得到的预测值是培训目标值的加权组合。它的潜在优点是通过研究数学公式,并通过严密的推导来寻找地震属性和目标测井曲线之间的关系。

概率神经网络技术和多层正向充填神经网络技术输入的数据相同,都包含一系列培训样本,设有3个地震属性,在分析时窗内有n个测井采样值:

式中:Li为目标测井曲线上第i个采样点的值;Aij为第i个地震属性的第j个采样点的值。

对于给定的培训数据,该网络假设新的输出测井值是地震属性的非线性组合,地震数据样本

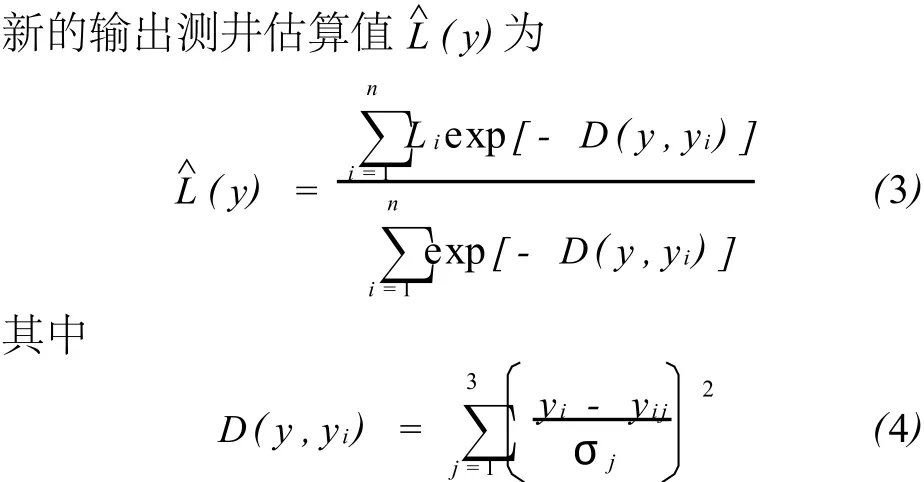
式中:D(y,yi)是输入点y与每一个培训点yi之间的变化量;σj为平滑参数;yij表示第i个采样点第j个属性。

预测的好坏主要取决于平滑参数,预测结果最优化的标准是实际的目标测井值与预测的目标测井值之间的误差最小。对于第m个目标采样点,新的输出测井值为:

由此可以计算每一个采样点的实际的目标测井值与预测的目标测井值之间的误差。对每一个采样点处理后总的累计误差EV(σ1,σ2,σ3)为:

误差的大小决定于平滑参数。

1.2 地质统计学随机模拟(反演)

地质统计学随机模拟是在地质统计学(空间信息统计学)基础上发展起来的一门技术。由于研究过程中涉及到的储层变量类型的不同,类型变量(离散变量,如沉积相、岩相)和连续变量(如孔隙度、渗透率、饱和度等)模拟方法有所不同。下面对具体工作中关系较为密切的几个个方面作以简要阐述。

1)地质统计学和随机模拟

地质统计学体系由4部分组成——区域化变量理论、空间结构变异性分析(变差函数)、克里金插值技术和随机模拟技术[3～5]。区域化变量理论阐述了地质统计学研究变量是空间位置的函数,空间变量具有确定性和随机性,不同空间位置变量相关性(空间变量变异性)与空间距离有关;空间结构变异性分析给出了研究空间变量变异性的工具——变差函数模型;克里金插值技术是在变差函数分析的基础上对未知区域进行插值的一门技术,其中包含了多种克里金算法。

随机模拟技术是在空间变异性分析和克里金技术的基础上,结合蒙特卡罗技术形成的一种对未知变量分布进行随机模拟的一种方法。简单而言,地质统计学研究的变量是随机的,经过空间变异性分析和克里金方程组的求解,可以获得空间某一未知点空间随机变量的累计概率分布函数,通过蒙特卡罗技术对该分布进行等概率的抽样,可以获得该点的一簇可能的变量值,为预测该点变量值提供依据。

2)连续变量的变差函数

变差函数是地质统计学方法中最常用的衡量储层变量空间变异性的工具。在储层建模过程中,综合各种不同来源的数据,研究变差函数的计算及理论拟合,是十分必要的。变差函数分析直接关系到建立储层模型的可靠性。这里对变差函数做简要介绍。连续变量Z(x)变差函数的数学表达式为:

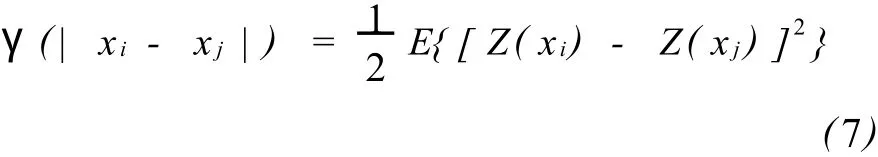
式中:γ(·)是半变差函数,一般直接称之为变差函数;E[·]表示数学期望;Z(xi)和Z(xj)是空间区域内两个位置的观测值。上式表明变差函数为空间两点的观测值差的平方的数学期望之半。

实际应用时估计变差函数采用下式计算:

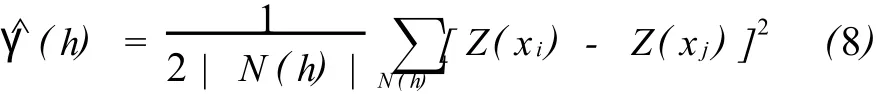
式中为估计变量函数;N(h)表示距离为h的点对个数。

图1示出了变差函数的主要参数。从图中可以看出,变差函数的一个基本参数是变程,当滞后距离h增大时,γ(·)的值随之增大,当γ(·)达到平稳值时的滞后距h值称为变程,它表示空间上的最大相关距离;另一个参数是基台值,即当γ(·)达到平稳值时的值,表示数值先验方差的大小,块金值是h=0位置的非零γ(·)值。可以看出,当h=0时,γ(·)=0,但实际上,还会出现块金值,产生这种现象的原因比较多,可能是由于采样和实验误差或小尺度的变化引起的。

3)类型变量的变差函数

在岩相参数等类型变量的变差函数求取前,首先要对岩相代码做一下指示变换,将岩相代码Z(x)转变为岩相指示代码I(x)(包含0和1两个值为例)。

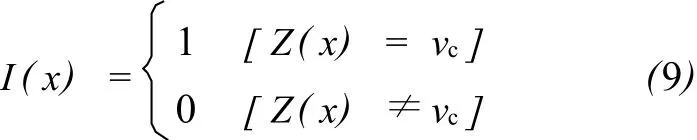
式中:vc为特定岩相代码值。

指示变差函数为:

实际应用时估计指示变差函数采用下式计算:

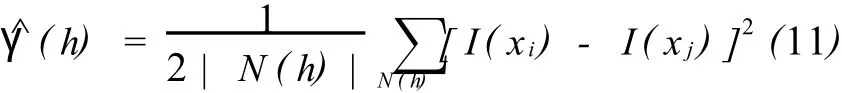
图1 变差函数主要参数示意图Fig.1 Main parameters of variogram

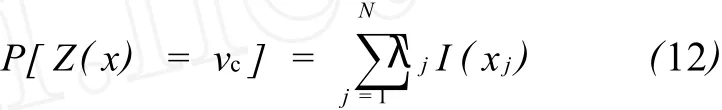
4)序贯指示模拟和序贯高斯模拟

在储层参数随机模拟过程中,类型变量多采用序贯指示模拟算法,连续变量多采用序贯高斯模拟算法。

序贯指示模拟的基本思想就是将地质信息进行离散的编码,通常编码成0与1两值的指示变量(两种类型变量为例),然后构建指示变量的变差函数模型,通过求解克里金方程组,得到指示变量的克里金估计。指示变量的克里金估计给出了未知位置变量的概率估计(通过解克里金方程组,权系数λj已知)。

式中:λj为权系数。

然后采用Monte Carlo技术对未知变量点进行赋值。对所有未知变量点按次序访问一遍得到随机模型的一个实现。

序贯高斯模拟是主要应用于连续型随机变量模拟的一种方法,属于参数估计的随机模拟方法。首先假定连续变量服从正态(高斯)分布,然后通过克里金估值技术确定正态分布的两个参数——数学期望和估计方差。其中数学期望为(通过解克里金方程组,权系数λj已知):

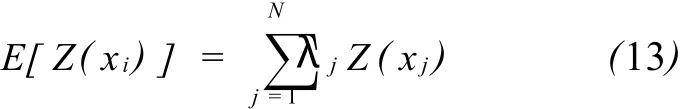
在确定了分布参数之后,对未知变量点通过Monte Carlo技术进行抽样赋值,对所有未知变量点按次序访问一遍得到随机模型的一个实现。

为了最大限度地充分利用或间接利用地震信息,在以上两种方法使用过程中,在克里金估计环节一般使用同位配置协克里金方法,将第二变量的影响考虑进去。如岩相模拟、孔隙度模拟时第二变量为波阻抗,在渗透率模拟和含气饱和度模拟环节第二变量为孔隙度信息。同位配置协克里金的估计值表达形式为:

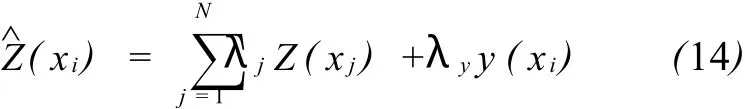
式中:λy为同位的主变量Z(xi)和第二变量y(xi)的线性相关系数。

1.3 二者结合的必要性

在神经网络多属性优化过程中,测井曲线被作为学习目标曲线,不参与到新属性的合成之中,其自身高频成分往往不能在优化属性得到直接的反映,因而优化属性只是多种地震属性的一种组合,垂向分辨能力较低。在地质统计学随机模拟(反演)过程中,测井信息是作为条件数据(硬数据)出现的,直接参与到模拟结果之中,因而具有较高的垂向分辨能力。在适用性上,在研究区钻井数目较少的情况下,如果钻井分布均匀,采用神经网络方法虽然分辨率低一些,但能较客观地预测储层参数的横向分布状态。地质统计学方法在钻井较为稀疏的情况下,很难对储层参数的变异结构做出较为合理的分析,因而往往会在平面图上出现“围井打圈”,剖面图上出现“圣诞树”或“平行轨道”等明显有悖于地质规律的现象。在储层、非储层阻抗差异微弱的情况下,由于“软数据”(地震数据)约束失效,会加剧以上不合理现象的出现。

考虑到二者的应用特点和适用情况,为了兼顾预测结果侧向上的客观趋势和垂向较好的分辨能力,如何将二者结合起来使用就成为研究工作当中需要考虑的问题。基于以上分析,结合D气田地震储层预测实际工作,笔者进行了将神经网络和地质统计学结合起来进行工作的尝试。

2 实际应用

2.1 应用需求

D气田是一个以上古生界致密碎屑岩岩性气藏为主的大型气田。储层地质地球物理条件较为复杂,储层砂体较薄(单砂体一般小于10 m)、侧向变化迅速。同时,目的层段砂泥岩阻抗差异微弱,地震资料主频较低(25～30 Hz),单从地震剖面上很难对储集体砂体做出预测。针对这种情况,研究中多种信息的利用成为优先考虑的问题。地震属性分析技术、基于地质统计学的储层参数反演技术得到了大量的应用并获得了较好的应用成效。但随着勘探开发的不断深入,储层预测的难度也在不断加大,如何在已有技术基础上进行优化现有方法技术,进一步减少储层预测多解性、提高储层预测精度就成为需要着重考虑的问题。

笔者在对已有技术分析的基础上认为,单一属性分析存在的主要问题是由原始地震数据带来的分辨能力不够、多解性强、缺少明确的地质含义;储层参数反演存在的主要问题是所使用的地震约束数据体(阻抗)对一些储层参数,如致密层段的岩性、孔隙度、含气性的分异度不够,从而导致在复杂层段和区域不能很好地起到侧向的约束作用,同时由于反演在时间域进行,需要分层段在空间域进行统计分析的参数模型很难求取准确。

2.2 应用方案

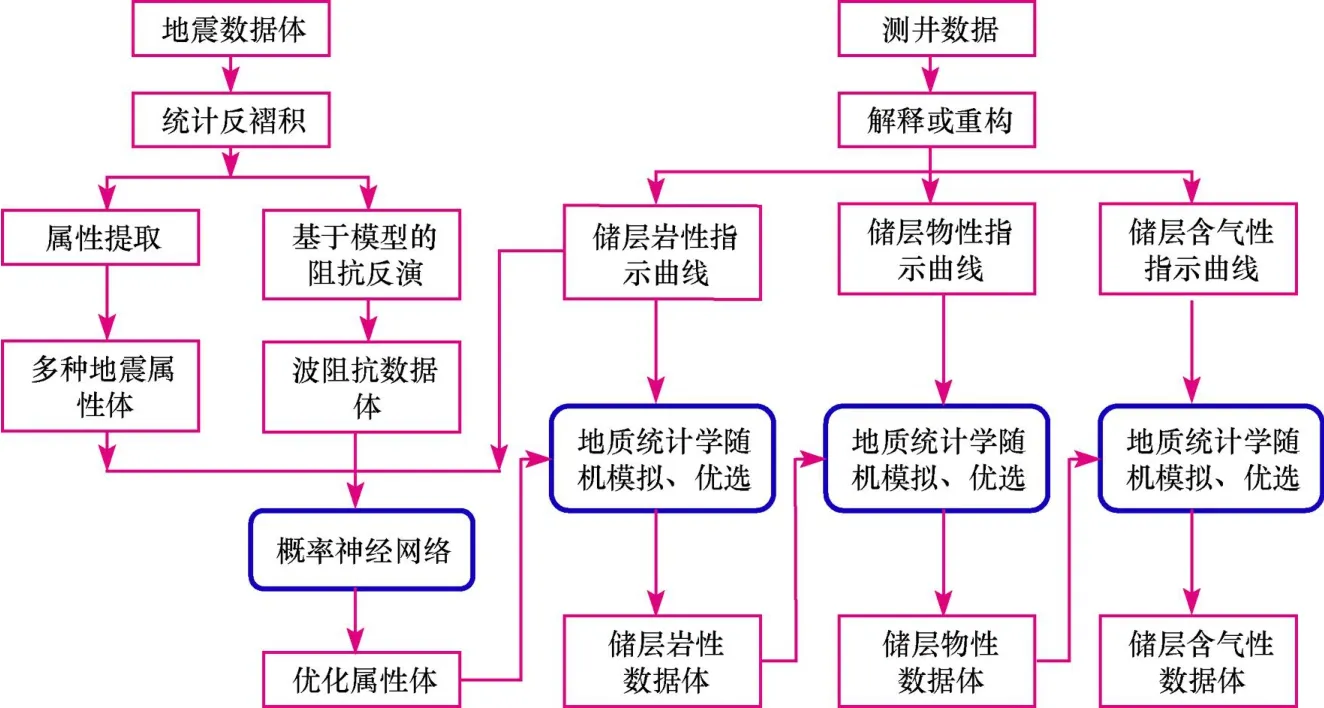
图2 神经网络和地质统计学整合多元信息流程图Fig.2 Flowchart showing the information integration based on artificial neural network and geostatistics

基于以上认识,应该在属性分析和参数模拟两个环节及两个环节的结合上进行研究方案的重调整。研究中应选择概率神经网络方法,以测井曲线作为学习目标,进行多种地震属性优化,获得地质含义较为明确的新的属性数据体。但是新的属性体的垂向分辨能力是不充分的。在此基础上,用新的优化属性体为约束,以测井数据作为条件数据(硬数据)进行储层参数地质统计学随机模拟(反演),最终得到较为精细,同时侧向分布合理的储层参数模型。在流程图(图2)中,岩性、物性、含气性(反演)模拟是分层次、逐级控制进行的,这也是与沉积地质学中对岩性、物性、含气性3者的关系相一致的。

2.3 流程调试和关键参数选择

应用概率神经网络,以重构的岩性指示曲线为目标测井曲线对地震属性进行了属性优化的相关分析工作。经过调试,最终确定了阻抗、二阶导数、绝对振幅积分、道积分、55～70 Hz信息、视极性、优势频率、瞬时相位余弦、瞬时相位9种地震属性作为敏感属性参与神经网络学习,学习得到的新的优化属性数据与重构的岩性指示曲线有较好的相关性,相关系数达到84.54%。从图3可以看出,优化属性与岩性指示曲线的相关性也较阻抗与岩性指示曲线的相关性有较大改善,单独由阻抗预测结果与岩性指示曲线的相关性仅有45.76%。而且因为优化属性以岩性指示曲线为学习目标进行了训练,因而具有明确的地质意义,低值(＜270)代表了砂岩的存在。图4给出了一条属性优化剖面,尽管垂向精度不够高,但较好地反映了砂岩侧向的展布趋势,可以作为岩性参数模拟的约束数据体。

在应用地质统计学进行储层参数反演(模拟)环节,最为关键的参数是各小层各岩相的变差函数模型,模拟是在深度域进行的,相应参数的空间统计得以较好地完成。

2.4 应用效果

在相关参数调试的基础上,依照图1所示的工作流程进行了相关工作,并按照随机模拟常用的模拟前后参数分布直方图最为近似的原则(“忠实于直方图”)进行了预测结果优选,最终得到了研究区目的层段的岩相、孔隙度、含气饱和度预测结果。图5显示了同一剖面的岩性、孔隙度、含气饱和度的分布状况。从剖面可以看到,薄层砂体的岩性、物性和含气性分布状况得到了较为精细的刻画。

以上研究成果被及时地应用到D气田井位部署工作之中,成为气田井位部署的主要参考依据之一。结合钻井情况分析,对储层参数模拟结果进行了钻井验证。

图3 阻抗预测结果(左)、优化属性预测结果(右)与岩性指示曲线相关性比较Fig.3 Correlations of predicted impedance(left)and optimized attribute(right)with lithology indicator curves

图4 属性优化剖面揭示的砂体侧向展布Fig.4 Lateral distribution of sandbody revealed by optimized attribute sections

图5 储层参数(岩性、孔隙度、含气饱和度)预测成果剖面Fig.5 Reservoir prediction profiles(lithology,porosity and gas saturation)

参加验证分析的未参与模拟的钻井共计20口,气砂岩厚度平均绝对误差值为0.36 m,平均相对误差值为13.72%。可见,预测结果准确率在85%以上,储层预测成果是较为可靠的。

3 结论

针对复杂地质地球物理条件下地震储层预测中遇到的多解性和精度问题,笔者从地震储层预测两种常用的信息融合工具——神经网络和地质统计学的原理出发,提出了将二者结合进行地震储层预测方案流程。结合D气田致密碎屑岩岩性气藏储层预测中遇到的实际问题,对该方案流程进行了验证性分析应用,应用结果表明,储层预测结果的精度较高,预测过程中的一些多解性现象得到显著改善,相关方案流程对于致密碎屑岩薄储层预测来说,是较为有效的。

1 侯景儒,尹镇南,李维明,等.实用地质统计学(空间信息统计学)[M].北京:地质出版社,1998.1～5

2 王家华,张团峰.油气储层随机建模[M].北京:石油工业出版社,2001.1～10

3 Pan Guocheng.地质统计学中的区域化变量理论[J].世界地质,1997,16(2):85～93

4 Pan Guocheng.地质统计学中结构分析的理论与方法[J].世界地质,1997,16(3):70～82

5 Pan Guocheng.地质统计学中的估值技术和条件模拟[J].世界地质,1997,16(3):83～10

6 刘振峰,郝天珧,杨长春.沉积模型和储层随机建模[J].地球物理学进展,2003,18(3):519～523

7 刘振峰.基于MRF模型的油气储层属性随机建模方法研究[D].中科院研究生院,2004.1～6

8 李军,熊利平,赵为永.基于确定性和随机模型的薄储层岩性预测[J].石油与天然气地质,2009,30(2):240～244

9 谯述蓉,张虹,赵爽.川西DY地区须家河组致密砂岩储层预测技术及应用效果分析[J].石油与天然气地质,2008, 29(6):774～780

10 许杰,何治亮,董宁,等.鄂尔多斯盆地大牛地气田盒3段河道砂岩相控储层预测[J].石油与天然气地质,2009,30(6):692～705

11 董宁,刘振峰,周小鹰,等.鄂尔多斯盆地致密碎屑岩储层地震识别及预测[J].石油与天然气地质,2008,29(5):668～675

12 Caers J,Ma X.Modelling conditional distributions of facies from seismic using neural nets[J].Mathematical Geology, 2002,34:143-167

13 Caers J,Avseth P,Mukerji T.Geostatistical integration of rock physics seismic amplitudes and geological models in North-Sea turbidite systems[J].The Leading Edge,2001,20 (3):308-312

Reservoir prediction with integrated information based on artificial neural network technology and geostatistics

Li Dongan1,Ning Junrui2and Liu Zhenfeng2
(1.Faculty of Resources,China University of Geosciences,Wuhan,Hubei430074,China;2.S INOPEC Petroleum Ex ploration and Production Research Institute,Beijing100083,China)

How to eliminate mistiness and improve the precision of seismic data interpretation is an everlasting topic in reservoir prediction.However,it is rather difficult to solve the problem due to the complexity of actual geological and geophysical conditions and low quality of seismic data.Recent study shows that integration of information from different sources is an effective way to deal with the issue.Guided by this understanding,we tried to combine artificial neural network technologies and geostatistics in reservoir prediction of the Dgas field. By doing so,we realized the integration of multiple seismic attributes with logging data,and effectively reduced the mistiness and improved the precision of prediction.

seismic attribute,artificial neural network,geostatistics,reservoir prediction

TE132.1

A

0253-9985(2010)04-0493-06

2010-06-28。

李东安(1963—),男,高级工程师,石油物探。

国家“十一五”科技攻关重大专项(2008ZX05002-005-003)。

(编辑 高 岩)