基于人工神经网络的ZK60镁合金热压缩变形行为

覃银江，潘清林，何运斌，李文斌，刘晓艳，范 曦

(中南大学 材料科学与工程学院，长沙 410083)

镁合金具有HCP结构，在室温下塑性变形仅局限于基面{0001}〉滑移和锥面孪生，因此加工十分困难，这大大限制了其应用领域。而在高温下变形时，由于非基面滑移和〈c+a〉滑移通过热激活而启动，使镁合金的塑性变形能力得到极大提高[1−2]。因此，研究镁合金热变形行为具有十分重要的意义。

流变应力是材料在热变形时的基本性能指标，无论在制定热加工工艺，还是在金属塑性变形理论研究方面都是极其重要的[3]。对流变应力的描述，通常是在大量实验的基础上，预先提出一个包含主要影响参数的经验关系式，然后用实验数据对数学关系式进行拟合。前人在拟合方法方面做了大量研究工作[4−9]，但该方法只能近似描述特定实验条件下的流变特征，推广能力较差，且计算工作量较大。材料加工过程中流变应力受变形温度、变形程度、应变速率和摩擦等众多因素的影响，属于典型的复杂非线性问题。人工神经网络(ANN)是近年发展起来的一种具有人工智能的系统，具有强大的处理复杂非线性问题的能力[10]。它提供一种与传统回归方法完全不同的处理流变应力的方法，其最大优势在于不需要预先给定数学关系式，而直接从已有的实验数据出发，经过有限次迭代计算得到一个反映实验数据内在规律的模型，能十分精确地逼近输入与输出间的映射，并能很好地反映预测对象的发展趋势。

目前，国内外已有一些关于采用人工神经网络研究流变行为的报道。韩丽琦等[11]采用人工神经网络预测热轧碳钢的变形抗力。刘雪峰和汪凌云[12]建立Al-Li合金高温变形稳态流变应力与应变速率和变形温度对应关系的人工神经网络模型。KAPOOR等[13]和REDDY等[14]分别采用人工神经网络模型研究了Zr-2.5Nb-0.5Cu与Ti-6Al-4V在不同相区的流变行为，与双曲正弦型的本构方程相比，所建模型具有更高的精度。BARIANI等[15]采用神经网络模型很好地预测Ni基合金热锻时的流变应力。PHANIRAJ和LAHIRI[16]以及WU等[17]运用ANN模型研究合金成分与变形参数对钢的热压缩流变应力的影响，所建模型具有很强的推广性。SHEIKH和 SERAJZADEH[18]建立考虑动态应变时效效应时AA5083铝合金人工神经网络流变应力模型，并应用实验验证模型的可靠性。但采用人工神经网络方法研究镁合金热变形行为的报道还很少。本文作者利用ZK60镁合金热压缩变形所得实验数据，建立描述该合金高温压缩变形流变应力变化规律的人工神经网络模型，并讨论变形参数对合金变形行为的影响。

1 实验

实验用ZK60镁合金的化学成分如表1所列，其铸态组织为平均晶粒尺寸约100 μm的等轴晶。铸态合金经673 K，12 h均匀化退火处理后线切割成d10 mm×15 mm的圆柱形试样。压缩实验在Gleeble−1500热模拟机上进行，通过自动控制系统在预设的温度和应变速率下进行恒温、恒应变速率压缩。试样压缩前的升温速度为10 ℃/s，在加热到预定变形温度之后保温 3 min。为减小试样与压头间的摩擦，在压缩试样两端分别加工一厚度为0.2 mm的凹槽以填充润滑剂，润滑剂组成为75%石墨(体积分数)+20%机油+5%硝酸三甲苯脂。实验应变速率为0.001、0.01、0.1和1 s−1，变形温度为200、250、300、350和 400 ℃，总压缩变形量为60%。

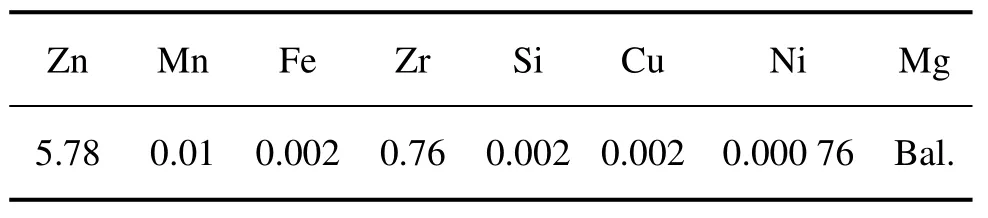
表1 ZK60镁合金的化学成分Table 1 Chemical compositions of ZK60 magnesium alloy(mass fraction, %)

2 ZK60镁合金流变应力的实验特征

图1所示为ZK60镁合金变形温度为200~400 ℃，应变速率为 0.001~1 s−1条件下的真应力—真应变曲线。从图 1可知，ZK60镁合金真应力—真应变曲线具有典型的动态再结晶特征。在实验应变范围内，真应力—真应变曲线可描述为如下4个阶段(见图2)：阶段Ⅰ(加工硬化阶段)，阶段Ⅱ(过渡阶段)，阶段Ⅲ(软化阶段)和阶段Ⅳ(稳态流变阶段)。在阶段Ⅰ(加工硬化阶段)，大量位错的产生和交互作用使晶体产生许多障碍和缺陷，阻碍了位错的进一步运动，合金变形抗力随应变增加而增大，此时加工硬化率大于软化率；在阶段Ⅱ(过渡阶段)，动态回复和部分动态再结晶的软化抵消了部分加工硬化，使合金的加工硬化率减小，当软化作用和硬化作用相等时，流变应力曲线达到峰值；在阶段Ⅲ(软化阶段)，动态再结晶软化作用超过加工硬化作用，使流变应力随应变增加而降低；当加工硬化与动态再结晶软化再次达到平衡时，流变应力即进入阶段Ⅳ(稳态流变阶段)。从图 1还可看出，在温度较高和应变速率较低时，合金很快发生再结晶，阶段Ⅱ(过渡阶段)变得不很明显甚至消失。

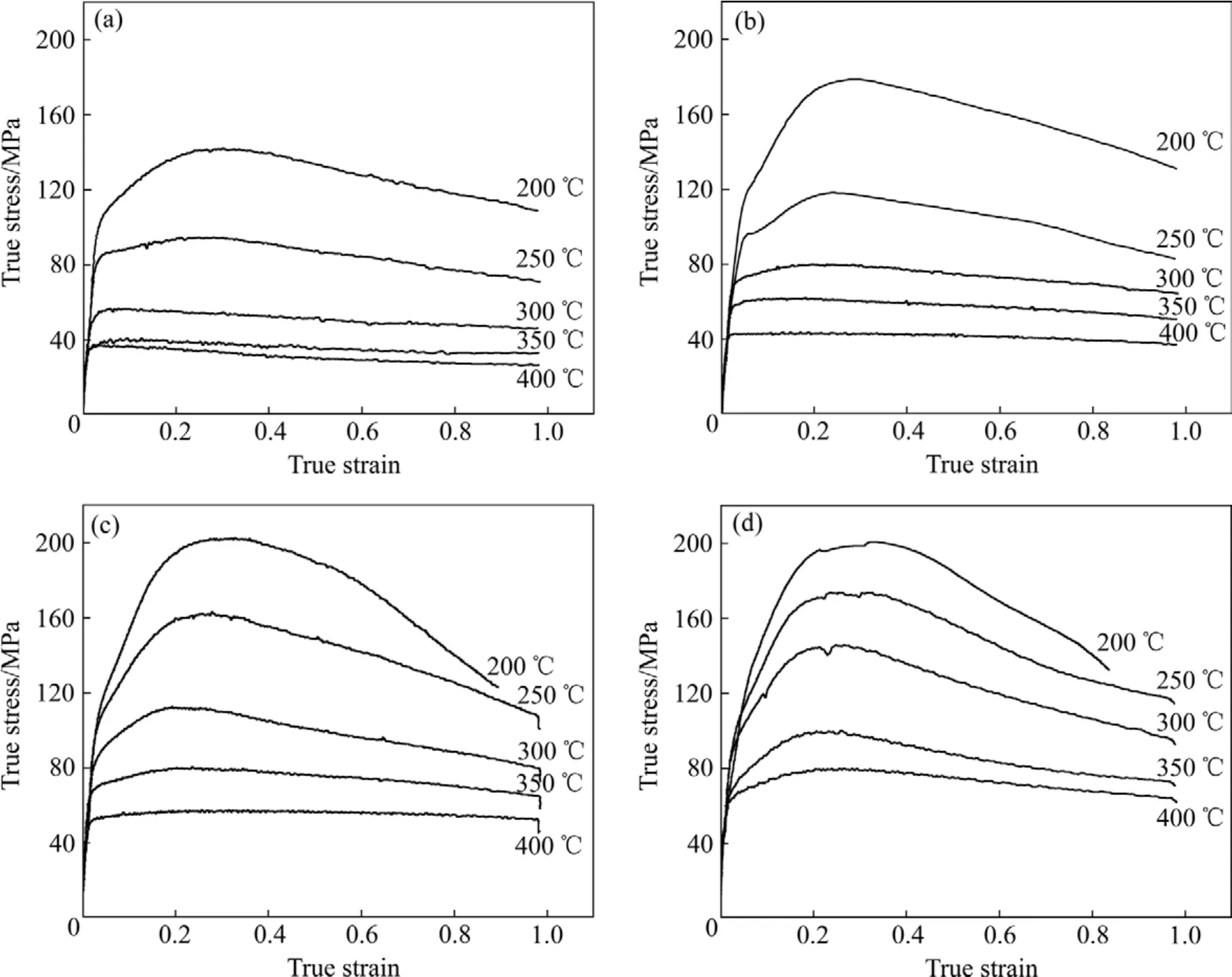
图1 ZK60镁合金在不同应变速率下的真应力—真应变曲线Fig.1 True stress—true strain curves of ZK60 magnesium alloy at different strain rates: (a) 0.001 s−1; (b) 0.01 s−1; (c) 0.1 s−1; (d) 1 s−1

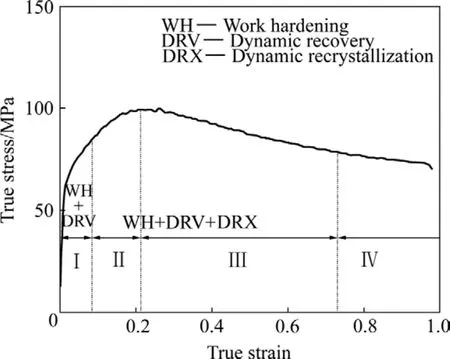
图2 ZK60合金在高温下的典型流变应力曲线Fig.2 Typical flow stress curves of ZK60 alloy at elevated temperature: Ⅰ—Work hardening stage;Ⅱ—Transition stage;Ⅲ—Softening stage; Ⅳ—Steady stage

3 人工神经网络(ANN)模型的建立

3.1 ANN结构的确定

本文作者采用一个多层前馈误差反向传播网络(BP网络)来建立ZK60镁合金流变应力本构模型。图3所示为一个三层BP网络的结构示意图，它包括输入层、隐含层和输出层。BP算法包括如下两个过程[19]：信息的正向传递和误差的反向传播。在正向传播过程中，输入信息从输入经隐含层计算传向输出层，如果在输出层没有得到期望的输出，则计算输出层的误差变化，然后转入反向传播。通过网络将误差信号沿原来的连接通路反传回来修改各层神经元的权值和阀值，直至达到期望目标。

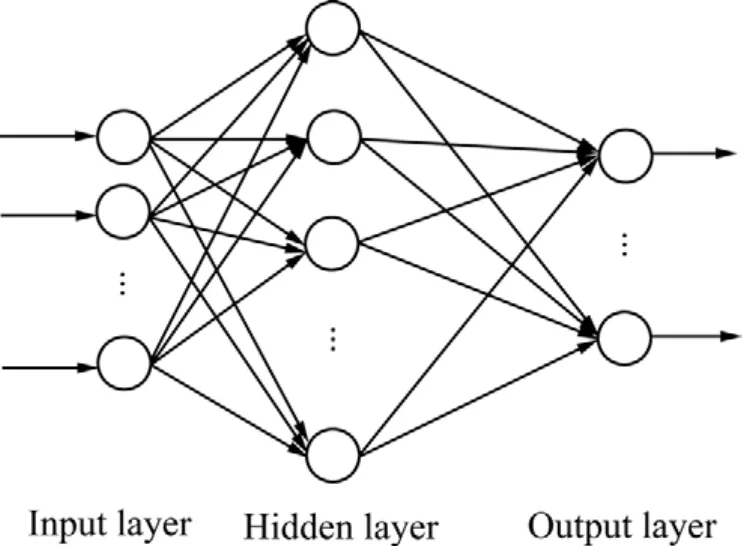
图3 前向ANN结构示意图Fig.3 Schematic diagram of structure of feed-forward ANN

根据ZK60镁合金高温压缩变形特点，确定网络输入分别为变形温度T，应变速率ε˙和应变ε，而流变应力σ为网络输出。对于隐层单元数的确定，没有理论依据可循，唯一公认的原则是能与给定样本符合的规模最小的网络就是最好的网络。本文作者采用试算法，计算不同隐层单元数条件下网络的均方误差，最终确定适宜的隐含层神经元个数为23。

经典的 BP算法实质是一种梯度最快速度下降静态寻优法，此法具有思路清晰、结构严谨等特点。但它的学习速度慢，且容易陷入局部极小，在实际应用中很难胜任。本文作者采用能够自适应调整学习率的Levenberg-Marquardt(L-M)算法对网络进行训练，大大提高学习效率。

3.2 样本数据及其预处理

本文作者从图1所示流变应力曲线中选取560组输入−输出数据来建立ZK60镁合金流变应力ANN预测模型。其中，随机选取的400组数据用来对网络进行训练，其余的160组数据在应变为0.1~0.8、步长为0.1处选得，用于对网络进行测试。这些数据的统计分析如表2所列。

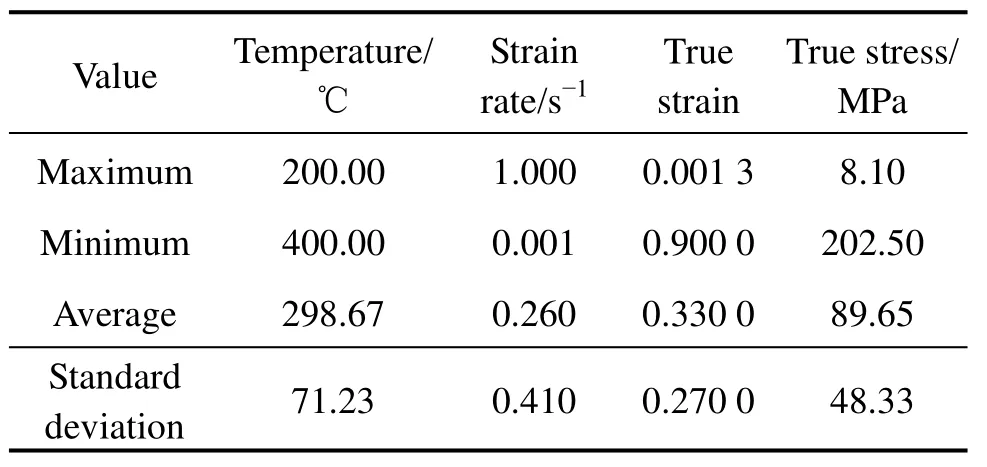
表2 输入与输出数据的统计分析Table 2 Statistical analysis of input and output data

为了避免网络模型迭代计算时数值过于集中在某些神经元和权值上而降低模型的计算精度，在神经网络训练之前，必须对所有的样本数据进行归一化预处理。本文作者采用如下的方程对变形温度T和流变应力σ进行归一化：

式中：X 为归一化前的数据；X′为与之对应的归一化后的数据；Xmax和Xmin为样本数据的最大值和最小值。由于应变速率ε˙变化较大，发生数量级的改变，如果采用式(1)对其归一化将归一化后的数据变得太小，神经网络不能很好地对其进行学习。因此，采用式(2)对应变速率进行归一化。由于应变值已经在0~1范围内，所以不需要再进行归一化处理。

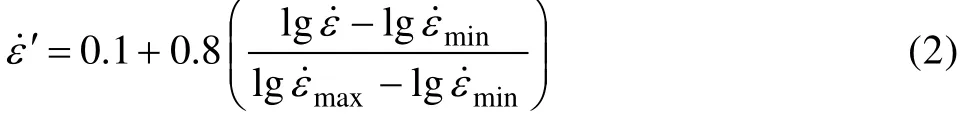
式中：ε˙为归一化前的应变速度；ε′˙为归一化后的应变速率；maxε˙和minε˙分别为应变速率的最大值和最小值。

4 结果与讨论

4.1 ANN模型性能评估

在本模拟中，流变应力模型经过1 545次迭代后收敛于预设的目标误差0.000 1，网络训练终止。采用不同的统计量对网络性能进行评估，它们分别是相关系数R，平均相对误差EA，均方根误差ER和发散因子S，表达式分别如下：

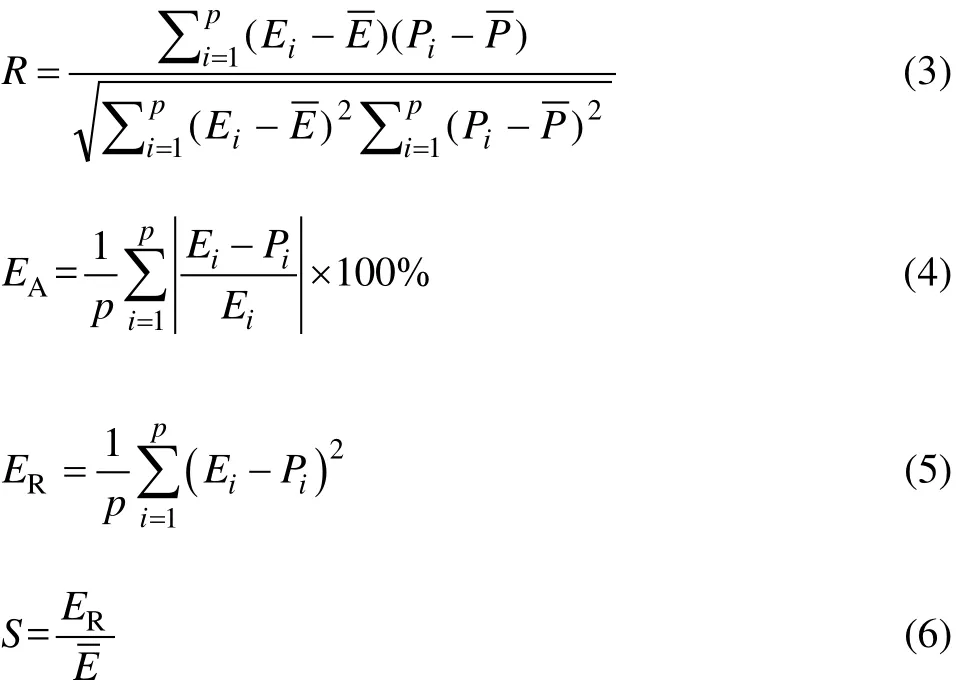
式中：Ei和Pi(i=1, …, p)分别为实验值和ANN模型预测值；p为样本总数；和分别为Ei和Pi的平均值。

相关系数R常用来表征实验值和预测值之间线性关系的强弱，但由于偏倚的存在，有时候高的R值并不是模型性能优良的充分条件[20]。因此，本文作者还采用ER和EA等无偏统计量来表征模型的预测能力。表3所列为采用以上统计量对网络性能进行评估的结果。由此可以看出，对训练样本和测试样本，模型的平均相对误差EA分别为2.70%和3.91%。这表明模型性能优良，具有很强的推广能力。采用该模型训练和测试得出的流变应力值与实验值的对比如图4(a)和(b)所示。由此可见，预测值与实验值吻合得很好，表明本文作者提出的神经网络模型可以很好地预测 ZK60镁合金的热压缩变形行为。

表3 ANN模型预测性能的统计分析

Table 3 Statistical analysis of performance of ANN model for training and testing predictions

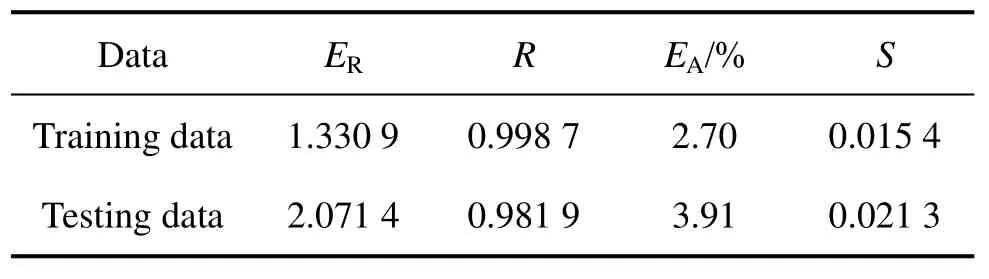
Data ER R EA/% S Training data 1.330 9 0.998 7 2.70 0.015 4 Testing data 2.071 4 0.981 9 3.91 0.021 3

为了更进一步分析采用 L-M 算法所训练网络的效果，对网络误差进行统计分析。对训练和测试的每一组样本分别计算相对误差，其计算式为

图 5所示为训练样本和测试样本的误差统计结果。结果表明，误差服从典型的Gaussian分布，误差平均值接近零。对90%以上的训练和测试样本，其预测值的误差均在±5%以内。这意味着预测误差的主要来源是实验数据的波动，而不能完全归咎于所建立的神经网络模型的预测能力。然而，在实验过程中，由于温度、应变速率和摩擦力等综合因素的影响，流变应力值的波动是不可避免的[21]。

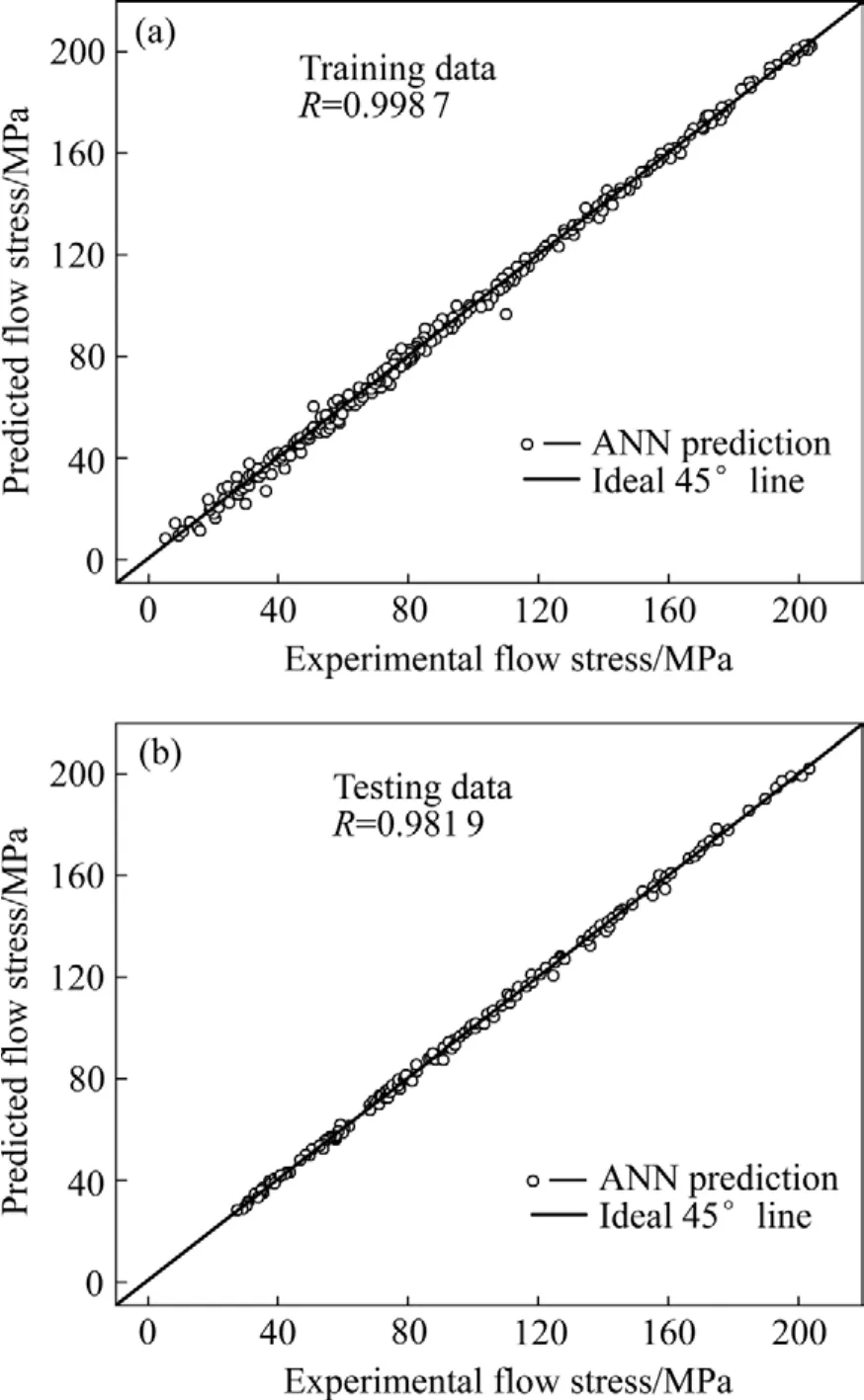
图4 ZK60合金流变应力实验值与ANN预测值的比较Fig.4 Comparison between experimental and predicted flow stress of ZK60 alloy using ANN: (a) Training data; (b) Testing data

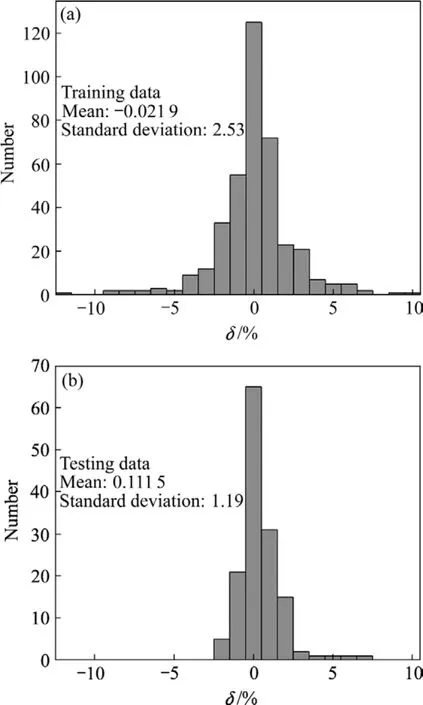
图5 采用L-M算法的ANN模型预测误差的统计分析Fig.5 Statistical analysis of error of ANN prediction employing L-M algorithm: (a) Training data; (b) Testing data

4.2 流变应力曲线预测

变形温度为 300 ℃和应变速率为 0.001 s−1时，ZK60镁合金的实验流变应力曲线与ANN预测值的对比如图6所示。由图6中可看出，ANN模型预测结果在图2所示的4个阶段均与实验流变应力曲线相符。这种方法避免常规的回归方法只能描述特定区域流变行为的缺陷。这再次证明所提出的模型可以十分精确地描述和预测ZK60镁合金的流变行为。该模型的缺点是，不能得出一个直观的数学表达式。但随着计算机技术的发展，在进行数值模拟和工程应用时可以直接运用所得到的ANN模型。

4.3 变形温度对流变应力的影响

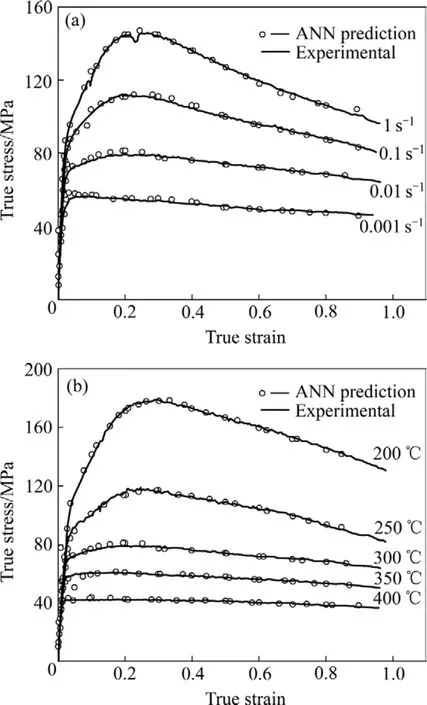
图6 ZK60合金实验流变应力实验值与预测值的比较Fig.6 Comparison between experimental and predicted flow stresses of ZK60 alloy using ANN: (a) t=300 ; (b)℃ ε˙=0.01 s−1

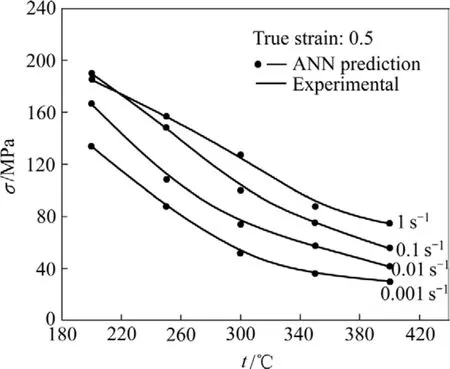
图7 温度对ZK60镁合金流变应力的影响Fig.7 Effects of temperature on flow stress of ZK60 magnesium alloy at different strain rates

采用本文作者提出的 ANN模型模拟变形温度对ZK60镁合金热变形流变应力的影响，其结果如图 7所示。从图7中可看出，预测结果与实验结果符合得很好。在应变速率相同时，随着变形温度的升高，流变应力降低，这与一般热加工理论得出的结果相符。因为当温度升高时，合金中原子热振动及扩散速率增加，位错的滑移、攀移及位错节点脱锚比低温时更容易，动态再结晶形核率增加，同时晶界迁移能力增强，这都将导致动态再结晶引起的软化作用增强，合金的流变应力降低。

4.4 应变速率对流变应力的影响

应变速率对 ZK60镁合金流变应力的影响也用ANN模型进行预测，其结果如图8所示。由图8可见，预测结果可以很好地符合流变应力σ与 ε˙ lg 之间的非线性关系。在同一变形温度下，随着应变速率的增加，流变应力升高。这主要是因为应变速率增加导致单位时间内产生的位错密度增加，合金的加工硬化作用增强。同时，合金的变形时间缩短，使得单位时间内动态再结晶的形核数目减少，软化程度下降，间接地也使合金的流变应力值增大。

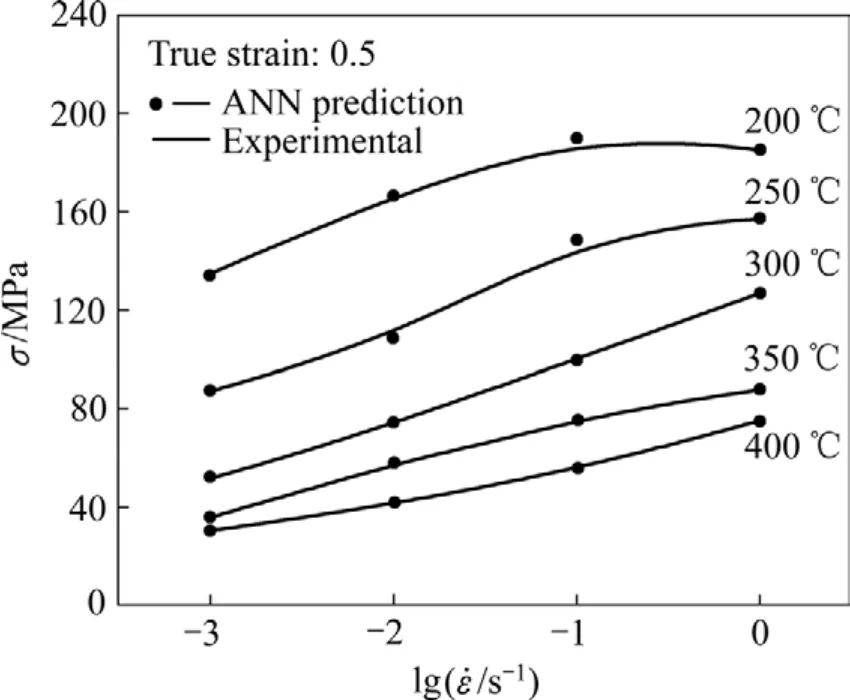
图8 应变速率对ZK60镁合金流变应力的影响Fig.8 Effects of strain rate on flow stress of ZK60 magnesium alloy at different temperatures

5 结论

1) ZK60镁合金高温压缩变形真应力—真应变曲线具有动态再结晶特征。应变速率一定时，流变应力随变形温度的升高而降低；变形温度一定时，流变应力随应变速率的增加而增大。

2) 建立描述ZK60镁合金流变应力的人工神经网络模型。模型为三层前馈误差反向传播网络，中间隐含层神经元个数为23，其输入参数分别为变形温度、应变速率和应变，输出为流变应力，采用 Levenberg-Marquardt算法对网络进行训练。

3) 模型预测的ZK60镁合金流变应力与实验值符合得很好，训练样本和测试样本对应的预测平均相对误差分别为 2.70%和 3.91%。预测变形温度和应变速率对流变应力的影响，其结果与一般热加工理论所得结果基本一致。

[1] SHENG Z Q, SHIVPURI R. Modeling flow stress of magnesium alloys at elevated temperature[J]. Mater Sci Eng A, 2006,419(1/2): 202−208.

[2] AL-SAMMAN T, GOTTSTEIN G. Dynamic recrystallization during high temperature deformation of magnesium[J]. Mater Sci Eng A, 2008, 490(1/2): 411−420.

[3] BARNETT M R. Influence of deformation conditions and texture on the high temperature flow stress of magnesium AZ31[J]. J Light Met, 2001, 1(3): 167−177.

[4] FOLLANSBEE P S, KOCKS U F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable[J]. Acta Met, 1988,36(1): 81−93.

[5] RAO K P, HAWBOLT E B. Assessment of simple flow stress relationship using literature data for a range of steels[J]. J Mater Process Technol, 1992, 29(1/3): 15−40.

[6] LASSRAOUI A, JONAS J J. Prediction of the steel flow stresses at high temperatures and strain rate[J]. Metall Trans A, 1991,22(7): 1545−1558.

[7] CINGARA A, MCQUEEN H J. New method for determining sinh constitutive constants for high temperature deformation of 300 austenitic steels[J]. J Mater Process Technol, 1992, 36(1):17−30.

[8] CINGARA A, MCQUEEN H J. New formula for calculating flow curves from high temperature constitutive data for 300 austenitic steels[J]. J Mater Process Technol, 1992, 36(1): 31−42.[9] HE X M, YU Z Q, LAI X M. A method to predict flow stress considering dynamic recrystallization during hot deformation[J].Comput Mater Sci, 2008, 44(2): 760−764.

[10] CAVALIERE P. Flow curve prediction of an Al-MMC under hot working conditions using neural networks[J]. Comput Mater Sci,2007, 38(4): 722−726.

[11] 韩丽琦, 臧 勇, 邹家祥, 章 博. 基于人工神经网络的热轧碳钢变形抗力预测[J]. 北京科技大学学报, 2001, 23(2):131−133.

HAN Li-qi, ZANG Yong, ZOU Jia-xiang, ZHANG Bo.Prediction of flow stress of carbon steel in hot strip rolling by artificial neural network[J]. Journal of University of Science and Technology Beijing, 2001, 23(2): 131−133.

[12] 刘雪峰, 汪凌云. 铝锂合金高温变形流变应力的人工神经网络模型[J]. 重庆大学学报: 自然科学版, 2001, 24(2): 68−71.

LIU Xue-feng, WANG Ling-yun. Artificial neural networks models for flow stress during high temperature plastic deformation of Al-Li alloy[J]. Journal of Chongqing University:Nature Science Edition, 2001, 24(2): 68−71.

[13] KAPOOR R, PAL D, CHAKRAVARTTY J K. Use of artificial neural networks to predict the deformation behavior of Zr-2.5Nb-0.5Cu[J]. J Mater Process Technol, 2005, 169(2):199−205.

[14] REDDY N S, LEE Y H, PARK C H, LEE C S. Prediction of flow stress in Ti-6Al-4V alloy with an equiaxed α+β microstructure by artificial neural networks[J]. Mater Sci Eng A,2008, 492(1/2): 276−282.

[15] BARIANI P F, BRUSCHI S, DAL NEGRO T. Prediction of nickel-base superalloys’ rheological behavior under hot forging conditions using artificial neural networks[J]. J Mater Process Technol, 2004, 152(3): 395−400.

[16] PHANIRAJ M P, LAHIRI A K. The applicability of neural network medel to predict flow stress for carbon steels[J]. J Mater Process Technol, 2003, 141(2): 219−227.

[17] WU R H, LIU J T, CHANG H B, HSU T Y, RUAN X Y.Prediction of the flow stress of 0.4C-1.9Cr-1.5Mn-1.0Ni-0.2Mo steel during hot deformation[J]. J Mater Process Technol, 2001,116(2/3): 211−218.

[18] SHEIKH H, SERAJZADEH S. Estimation of flow stresses behavior of AA5083 using artificial neural networks with regard to dynamic strain ageing effect[J]. J Mater Process Technol,2008, 196(1/3): 115−119.

[19] LIN Y C, ZHANG J, ZHONG J. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel[J]. Comput Mater Sci, 2008, 43(4): 752−758.

[20] SRINIVASULU S, JAIN A. A comparative analysis of training methods for artificial neural network rainfall-runoff models[J].Appl Soft Comput, 2006, 6(3): 295−306.

[21] CHUAN M S, BIGLOU J, LENARD G, KIM J G. Using neural networks to predict parameters in the hot working of aluminum alloys[J]. J Mater Process Technol, 1999, 86(1/3): 245−251.