让数学思想滋润学生的心田

李　新

名师档案

李新，1970年10月出生，中共党员，中学高级教师，江苏省小学数学特级教师，江苏省教育系统先进工作者，苏州市名教师，吴江市实验小学副校长。

他多次参与或承担苏州市与江苏省级的课题研究，论文在省、国家级刊物上发表或获奖的有60多篇。承担市、省、全国级的公开课20多次，获省级评课一等奖，多次应邀赴省外讲学。受到好评。2008年暑期担任教育部援助西藏中小学骨干教师培训班讲课专家和中西部农村中小学教师国家级远程培训主讲专家，圆满完成了任务。是九年义务教育课程标准实验教科书小学《数学》(江苏教育版)教材的编委，全程参与1-12册教材的编写工作。热忱培养青年教师。指导多名青年教师成长为吴江市、苏州市的骨干教师。

【教学内容】

苏教版义务教育课程标准实验教科书《数学》六年级(上册)第1页例1，并完成“练一练”和练习一第1～5题。

【教学目标】

1使学生经历探索运用方程解决较复杂的实际问题的过程，能将实际问题抽象成数学表达，并建立形如ax±b=c的方程，进而解决问题，初步体会建模思想。

2使学生经历探索运用等式的性质解形如ax±b=c的方程的过程，能将形如ax±b=c的方程逐步转化成形如x=a凸的形式。初步体会化归思想。

【教学过程】

一、引入

谈话：西安是我国的一座历史文化名城。那里名胜古迹众多，其中就有闻名遐迩的大雁塔和小雁塔(用课件出示大雁塔和小雁塔的图片)。这节课我们就先来研究与这两座塔有关的数学问题(用课件出示例1的文字部分)。

二、探索

1找数量间的相等关系。

(指名读题)

师：通过读题。你知道大雁塔和小雁塔的高度之间有什么关系吗?

生：大雁塔高64米。比小雁塔高度的2倍少22米。(教师用课件呈现“大雁塔的高度比小雁塔高度的2倍少22米”)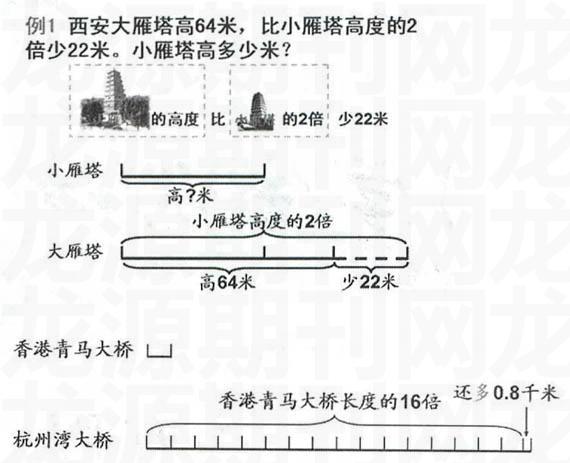

师：如果要用一幅线段图来表示大雁塔和小雁塔高度之间的关系。可以怎样画?同桌讨论一下。

生：我先画一条线段表示小雁塔的高度。

师：为什么呢?

生：因为可以把小雁塔的高度看作1份，任意画一条线段来表示，再画表示大雁塔高度的线段。

师：(课件演示画图的部分过程：先画一条线段，表示小雁塔的高度，再画出小雁塔高度的2倍)你们能接着画下去吗?请看老师发给你们的练习纸，上面已经画好了和银幕上一样的图。请根据“大雁塔的高度比小雁塔高度的2倍少22米”，接着画下去。(学生画图，教师巡视)

师：(用实物投影展示一名学生画的图)你能说说为什么要这样画吗?

生：(边指图边说)这是小雁塔高度的2倍，大雁塔的高度比小雁塔高度的2倍少22米，所以从这里往回画22米。

师：那么，哪一段表示了大雁塔的高度?

生：(指图)从这里到这里。

师：和他一样画、一样想的同学请举手。(大多数学生举手)

师：请大家看银幕(银幕上有如下内容)，现在银幕上有一个问题、一句话、一幅线段图。根据这些内容，你，能找出大雁塔与小雁塔高度之间的相等关系吗?可以先在小组里讨论一下。

生1：小雁塔的高度x2-22=大雁塔的高度。

师：(板书这一关系式)你是怎么想到这个关系式的?

生1：我是看着图想的。

师：能说说想的过程吗?

生1：我看到最下面的线段。“小雁塔高度的2倍”去掉“22米”就是“大雁塔的高度”。

生2：我是看着中间那句话来想的，因为“大雁塔的高度比小雁塔高度的2倍少22米”。所以就用“小雁塔高度的2倍”减“22米”等于“大雁塔的高度”。

师：两位同学的想法都很好。请用其中一种想法再想一遍，并和同桌说一说想的过程。

师：大雁塔与小雁塔高度之间的这种相等关系。你还能用别的等式来表示吗?

生：我用大雁塔的高度先加22再除以2。

师：(指线段图)大家看，“‘大雁塔的高度+22”跟什么是相等的?

生：大雁塔的高度+22-小雁塔的高度×2。

师：(板书这个关系式)讲得非常好!我们找到第二个等式来表示两座塔高度之间的相等关系了。还能找到第三个吗?(学生都不举手，多数脸上有疑惑的表情)那么这样，老师提示一下，这个等式的一边是“22米”，大家想，另一边可以写上怎样的式子，能和“22米”相等?

生：小雁塔的高度x2-大雁塔的高度=22。

师：谁能对照线段图或这句关键的话。分析一下这个关系式是否正确?

生1：“大雁塔的高度”比“小雁塔高度的2倍”少，所以用“小雁塔高度的2倩”减“大雁塔的高度”。

生2：我看线段图可以知道，“小雁塔高度的2倍”减“大雁塔的高度”等于22米。

2.列方程。

师：我们先看最先找到的关系式：小雁塔的高度x2-22=大雁塔的高度。在这个关系式中，已知“大雁塔的高度”是64米，求“小雁塔的高度”：像这样的题，适合用什么方法解答?

生：用方程解。

师：怎样设未知数呢?根据这个等量关系怎样列方程呢?同桌讨论一下。

生：设小雁塔高x米。2x-22=64。

师：这个方程的左边表示什么?右边呢?

生：左边的“20x”表示“小雁塔高度的2倍”。减22米后就是“大雁塔的高度”；右边是“大雁塔的高度”。

师：所以说这个方程左右两边表示了同一个数量。符合题意，是正确的。

3解方程。

师：这个方程和以前学过的方程有什么不同?

生：以前学过的方程左边只有一步。这个方程左边有两步。

师：你能联系实际问题，运用以前学习的知识，想出解这个方程的第一步吗?请动笔写一写。

(学生尝试解方程，教师巡视指导)

生1：2x-64+22。因为“2x”是“小雁塔高度的2倍”。它就等于“大雁塔的高度”加“22米”。

生2：我也认为2x=64+22。但我是这样想的。方程的左边要先算“2x”，就把“2x”当作一个整体，这样，方程的两边同时加22，就得到2x-64+22。

师：其实，×××(生1)的解法正好说明×××(生2)的解法是正确的。由于“小雁塔高度”未知。“小雁塔高度的2倍”也就未知，就可以把它看作一个整体。这样。原来的方程就可以看作是“一个整体22=64”。就能运用等式的性质来解了。请大家把这种想法和同桌说一说，然后把这个方程继续解完。

生：2x=86，x＝86÷2，x＝43。

师：这个方程的左边有两步，解这个方程时，最关键的步骤有哪些?

生：把2x看作一个整体，方程两边同时加22；方程变成2x=86后，两边再同时除以2。

师：大家看，方程两边同时加22后，方程左边由两步变成了一步；方程两边再同时除以2后，方程左边只剩下x，右边是43，就表示方程解完了。其实解方程的过程就是不断运用等式的性质等知识，把原来比较复杂的

方程变得越来越简单，一直简单到“2x等于几”的形式。

师：谁能检验一下，结果是否正确?

生：把x＝43代入原方程。左边=2x43-22=86-22＝64，右边=64，左边=右边，所以x=43是原方程的解。

师：一开始我们检验了所列的方程是正确的。现在检验了结果也是正确的。所以，小雁塔高43米。

4小结。

师：谁能回顾一下，我们刚才用方程解决问题主要经历了哪些骤?

生1：先找到了大雁塔与小雁塔高度之间的相等关系。

生2：然后设未知数为x，并列出方程。

生3：再根据等式的性质解方程，并检验，最后写出答案。

师：(结合学生口答，板书：找、设、列、解、验、答)你觉得这些步骤中。最关键的什么呢?

生：找数量问的相等关系。

5列不同的方程。

师：对这个问题，开始我们还写出了另两种关系式。请任意选一个关系式，也设小雁塔高x米，列出方程，并求出方程的解。

(生列方程、解方程)

生1：2x=-64+22，2x＝-86，x＝86÷2，x＝43。

生2：2x-64=22，2x=22+64，2x~=86，x=-86÷2，x=43。

师：观察3个解方程的过程，有什么相同的地方?

生：都有2x=86这一步。

师：原来都是比较复杂的方程。运用等式的性质或经过计算，都变成相同的简单方程。所以说，3个方程虽然是依据不同的等量关系所列，但实质上还是相同的。相比较而言，哪个方程所依据的等量关系思考时更顺一些?

生：2x-22=64。

三、练习

1完成“练一练”。出示一幅线段图：

师：能用一句话说明线段图所表示的数量关系吗?

生：杭州湾大桥全长比香港青马大桥的16倍还多0.8千米。

师：杭州湾大桥已经建成。它是目前世界上最长的跨海大桥，全长36千米。你能用方程求出香港青马大桥的长度吗?

(生解决问题)

生1：解：设香港青马大桥长x千米。16x+0.8=36.16x=36-0.8，16x=35.2。x=2.2。

师：你根据什么等量关系列的方程?

生1：香港青马大桥的长度×16+0.8=杭州湾大桥的长度。

师：谁能说说解这个方程，第一步可以怎样想?

生2：把“16x”看作一个整体，方程两边同时减0.8。

师：结果是否正确，怎样检验?

生3：16×2.2+0.8=35.2+0.8=36。

师：这个“练一练”和例题有什么相同的地方?

生1：都要根据等量关系列出方程解答。

生2：列出的方程左边都有两步计算。

师：而且都是“几x”加或减几。那么解方程时有什么相同的地方?

生1：都要把“几x”看作一个整体。

生2：都要两次运用等式的性质。

2完成练习一第1题。

请学生看书上的题，独立完成。教师巡视。请一位学生将解第(2)题“108+7x=3.9”的过程写在黑板上，集体评讲。

3完成练习一第2题。

请学生看书上的题，独立完成第(1)题的填空，教师巡视，发现有些学生不会填。组织集体讲评，课件逐步呈现如下内容，指导学生思考。再让学生独立完成第(2)题，交流思考过程。

4完成练习一第3题。学生看书上的题，独立完成。展示学生的作业，请学生说想的过程。

四、作业与总结(略)