图示教学法在数据结构与算法教学中的应用

沙宗尧 边馥苓

摘要:数据结构和算法的教学是计算机科学与技术、软件工程等相关专业最重要的教学内容之一,特别是在复杂的算法分析时,由于具有抽象性和较强的逻辑性,不采用好的教学方法,往往是事倍功半。本文提出用图示教学法教授数据结构中的算法,并以图状结构中的最小生成树算法为例,详细介绍了该图示方法描述数据结构算法过程,可以为数据结构的教学提供参考。

关键词:数据结构;算法;图示教学法;最小生成树

中图分类号:G642 文献标识码:B

1背景

数据结构和算法是计算机科学与技术、软件工程等相关专业的专业基础课,其重要性不言而喻,在教学过程中需要运用多种教学方法,让学生领会算法实现的过程和本质,加深对所学知识的理解、记忆和应用。在数据结构和算法课程教学中,图状结构的教学是一个难点,特别是涉及到图的具体应用时,更让学生难以掌握,本文将图示教学法应用到数据结构中关于图状结构的一个典型应用——最小生成树问题,给出该教学方法的基本方法和过程,取得了良好的教学效果。

最小生成树是图状(网络)结构中一个典型的实践应用,可以解决实际中诸如公路网的规划,即在n个城市中,如何规划n-1条公路,使得n个城市都可以连接起来,而所有城市间的连接线长度的总和最短(所要修建的公路长度最短,因而费用最少)。

对于这个典型的应用,绝大多数教科书均介绍了普里姆(Prim)算法,用于求最小生成树问题,然而教科书对这个算法实现的论述,一般是先介绍应用背景,然后就给出算法实现的过程,缺少形象的算法分析过程,课堂教学讲解如果按照这种方式去传授,学生在理解上十分吃力,而且不能有效地长期记忆。笔者结合自己在教学中的经验,将以上算法采用了图示教学法来分析其基本原理和实现过程,并给出算法实现过程,取得了良好的效果。

2教学方法

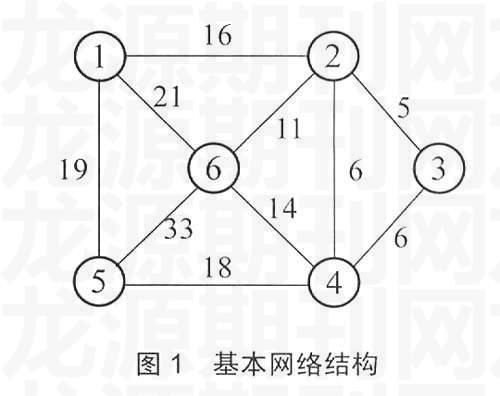
图示教学法就是用各种图形表示的方法描述问题、引导学生的思考,增强对新知识的记忆,并在教学中被广泛使用。最小生成树属于网络的实践应用,下面以图1为例,用图示教学法来对最小生成树算法进行图示过程分析。

假设某一区域内有n个城市,现要为这些城市修建城间公路,使得任意两城市间都能够相互通达(连通),由于要求所有的城市都在该公路网上,某两个城市间的道路称为一个路段,则修建的道路路段总数应等于n-1个(容易理解:如果路段总数小于n-1,则会有存在城市不能处在该道路网的节点上;如果路段总数大于n-1则会存在某两个城市间有至少两个路段,则路段距离的总和将不是最小),先从这些城市中任选一个作为种子,把剩下的城市用路段连接到由该种子城市为起始点的城市网络中,保证路段长度总和最小(最优路段网),则最后连接好的路段即为最小生成树。

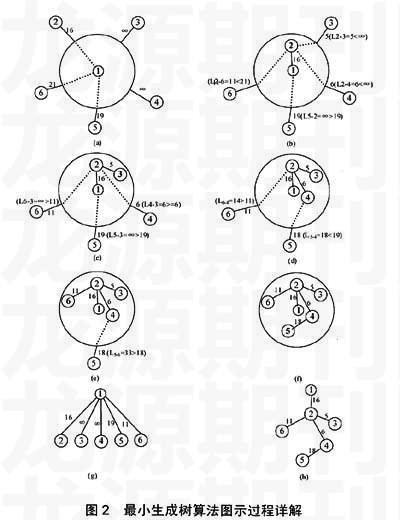
如图1,每个带圈的数字表示一个城市,城市间的边表示城市间的距离,如果两城市间没有边存在,则表示这两个城市间不适宜修道路(如有山脉或河流隔断,造价太高),假设种子城市为数字1(选定的网络的起始顶点),通过图示教学法求最优路段网的过程如图2:

图中,Li-j表示城市i与城市j间的距离,例如在(b)中,当把城市2加入到最优路段网后,城市3、4、6与该最优路段网的距离发生了变化,例如城市3,由于由L1-3(=∞)> L2-3(=5),故其与最优路段网的距离由原先的∞也转变为5

首先构造一个初始最优路段网,但该网络只有一个节点,即“种子城市”,其位于图2(a)中的中心圆圈内,圈外的节点称为外围节点或外围城市。然后根据图1城市间的距离(网络节点间的边的权值),求其它所有城市(网络节点)与种子城市间的距离(通过访问网络的物理存储结构如邻接表获取),该图表示仅通过了种子城市来连接所有的外围其它城市,图中中心圆圈外的城市当前还没有加入到最优路段网规划中,圈外连接每个外围城市与中心圆圈的实线表示该城市如果按当前规划方案加入到该路段网时所需要建造的路段长度(即网络边的权),圈内的虚线表示当前外围城市通过某一个最优路段网中的某城市为“桥梁”,而进入到该网络中。例如,城市2如果通过城市1进入规划网,则需要修建长度为16(仅表示相对数值)的道路,城市5要修建长度19的道路,城市6要修建长度21的道路,而城市3和城市4无法通过城市1来连接到最优路段网中(距离为无穷大,∞),而必须通过其它城市作为“桥梁”,来进入该规划网络中。很明显,如果按照该方案来把所有的外围城市都加入到初始最优路段网,得到的路段网如图2(g),需要修建的路段网总长度为∞,显然不是最优路段网。

注意到为了使规划的路段网是最优的(路段长度总和最小),只要保证每次加入到最优路段网中的城市都具有最短路段长度,则最后的路段总长度也必然最小。在图2(a)中,城市2与种子城市具有最小的距离(16),因而不可能找到其它任何一个路段,实现“种子城市与其它外围城市实现互连时,种子城市到其它任意一个城市的路段距离小于该值”,因而路段②-①必然是满足种子城市连通其它城市的最优路段,将城市2加入到最优路段网后,得到图2(b)。注意到当城市2加入到最优路段网后,城市3、4、6如果是通过城市2为“桥梁”(图中的虚线所示),加入到该最优路段网中,可以使各自的路段长度由原先的∞、∞和21分别缩短到5、6、11(其它城市通过城市2无法实现路段长度缩短,因为保持不变),此时路段总长度也由原先的∞缩小到57(即16+5+6+19+11),较图2(a),该方案有了很大的进步。然而该网络仍不是最优路段网,因为其仅保证了路段②-①的最优性(注意圆圈内的网络是最优的),而其它城市到该网络中的路段并非最优,这样不能保证路段总长度最小。

进一步注意到,在所有的当前外围城市中,城市3距离最优路段网的距离最短(5),也就是为了使当前最优路段网(圆圈内的城市及连线)与其它外围城市能够实现连通,且连通后的路段总长度最小,所以当前应加入城市3(图2(c))。城市3的加入或许可以使得其它的外围城市通过该城市为“桥梁”,而缩短外围城市到最优路段网的距离(当然这里城市3的加入实际并没有使其它城市到最优路段网的距离缩小)。同样的道理,在第4步(图2(d)),将城市4加入到最优路段网中(因为在余下的外围城市中,城市4到最优路段网的距离最小),该城市的加入,也使得城市1以该城市为“桥梁”而到最优路段网的距离由原来的19缩短到18(其它路段不变)。第5步将城市6加入到最优路段网中(图2(e)),该城市的加入没有影响余下的城市(当前仅剩一个城市,即城市5),最后将城市5加入到最优路段网中(图2(f))。得到的最终的最优路段网如图2(h),其路段长度的总和为56(16+5+11+6+18)。

3算法求解

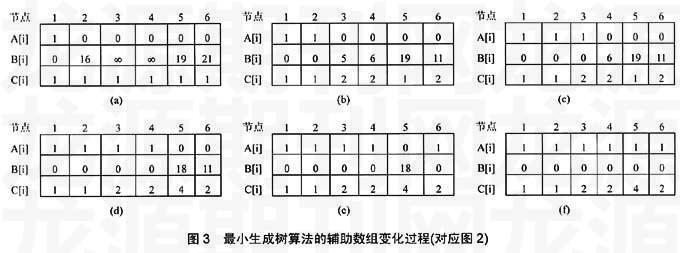
有了如上的图示教学法描述的计算最小生成树实现基本过程,在讲解算法时就比较容易了。算法在实现时需要构造三个辅助数组:第1个数组A[n](n为节点数)记录当前节点是外围节点还是已加入最短路段(路径)网的节点,数组元素A[i]=0或1,0表示节点i是一个外围节点,当加入到最短路段(路径)网后,A[i]=1;第2个数组B[n]记录各节点到最短路段(路径)网的距离,用B[n]表示;第3个数组C[n]记录外围节点通过最短路段(路径)网内的哪一个节点为“桥梁”而进入该路段(路径)网的。注意这里的路径R和路段L是两个不同的概念,路段是节点的边,而路径是具有共同节点的有序边起节点与尾节点首尾相连在一起的序列,如在图1中,其中的一个路径R1-3=L1-2+L2-3。下面结合图2和图3,给出这些数组的值在计算过程中的变化情况。

辅助数组的变化情况如下图3所示,其中图3(a)即对应于图2(a),图3(b)对应于图2(b),依此类推。在图3(a)中,首先只有第一个节点进入最短路段网,因此A[1]=1,其它的A元素均为0,外围节点与最短路段网的距离B[i]与图2(a)中的距离对应,这里节点1由于已在最短路段网,所以B[1]=0,由于所有的节点目前都是通过节点1与最短路段网连接,因而所有的C[i]的值都是1。在图3(b)中,由于节点2距最短路段网的距离最小(16),节点2进入最短路段网,因而A[2]=1,此时由于节点2已进入最短路段网,因而B[2]=0,而节点3和节点4通过节点2,使它们距最短路段网的距离由原先的∞缩短到5和6,节点6也通过节点2使B[6]由21缩小到11。图3(c)、3(d)、3(e)、3(f)的过程不再赘述。最后的结果(图3(f))表明,节点1通过其本身进入最短路段网,节点2通过节点1进入最短路段网,节点3、4、6均通过节点2为“桥梁”进入最短路段网,而节点5通过节点4进入最短路段网。

基于上述分析,不难给出以上算法的实现描述:

(1) 初始化数组A、B、C,结果如图2(a)、图3(a),这里假设以节点1为起始(源)节点,共有n个节点。

(2) 反复执行如下操作:将B[i]中值最小的元素对应的编号i(即节点i)放入A中(即修改A[i]为1),然后修改A[j]!=0(j!=i)对应的B[j]和C[j]的值,修改的依据是:如果B[j]>Li-j,则用B[j]的值更改为Li-j。直至所有的A[i](1<=i<=n)都是1为止。

(3) 输出结果,将B、C的最后值输出即可以得到最后结果,B所有的元素最后都为0,表示所有的元素都进入了最短路段网(最小生成数网),而C中的元素值表示的是当前节点元素(即节点1、2、3、4、5或6)是通过C中表示的节点编号而进入最短路段网的,即:节点1是通过其自身进入路段网,节点2通过节点1进入路段网,节点3、4和6均通过节点2进入路段网,节点5通过节点4进入路段网。

4结论

本文提出将图示教学法可应用于数据结构和算法课程教学的多个环节中,有些算法在大多数教科书中有了一定的图示过程表示,而有些算法却没有给出形象的图示表示,因而需要在教学中应补充。本文以图状结构中的最小生成树算法为例,通过图示分析,详细地讲解这个算法的核心思想和实现过程,通过视觉刺激,使学生能够加深对这个算法过程的把握,取得了良好的教学效果。

参考文献:

[1] 戴敏,于长云,董玉涛. 高效学习数据结构[J]. 计算机教育,2006(2):59-60.

[2] 余腊生,石献. 基于创新理念的数据结构教学方法探讨[J]. 计算机与信息技术,2006(11):110-114.

[3] 黄毅蓉. 关于多元复合函数偏导数链导法则的图示教学探讨[J]. 成都航空职业技术学院学报,2001(1):31-33.

[4] 薛超英. 数据结构[M]. 2版. 武汉:华中科技大学出版社,2002.