结构阻尼比对高速列车作用下桥梁动态响应的影响
2009-12-10沈永斌胡希冀亢元元
沈永斌 胡希冀 亢元元
摘要:车桥动态响应问题随着越来越多动车组的运行日益受到工程界的关注。通过有限元分析软件建立桥梁有限元模型,以移动质量模拟车辆,对不同工况下高速行驶的列车与简支桥梁的动力响应进行了研究和比较,得出了阻尼比对桥梁震动的影响。
关键词:高速列车;简支梁桥;移动质量
中图分类号:U441.3文献标识码:A文章编号:1000-8136(2009)29-0044-02
随着行车速度的不断提高,交通密度的不断增加,荷载的不断加重,交通车辆与结构的动力相互作用问题越来越受到人们的重视。特别是近年来越来越多的高速铁路相继投入运行。一方面,高速运行的车辆对所通过的结构物产生动力冲击作用,直接影响其工作状态和使用寿命;另一方面,结构的振动又对运行车辆的平稳性和安全性产生影响。
常见的对车辆的简化有以下几种形式:①将车辆荷载简化为集中力,在梁上移动;②将车辆简化为移动质量;③将车辆简化为移动的简谐力;④将车辆看作是在桥梁上移动的弹簧上的质量。这几种简化方法中。以移动弹簧上的质量模拟最为合理,但也最为复杂,而将车辆看作移动的集中力即移动荷载和移动质量这两种简化方式最为简单,但是在对桥梁进行初步估算时不失为最简便、快捷的方法。

本文通过建立移动荷载和移动质量的模型,采用有限元软件ANSYS来研究和比较车辆在不同阻尼比的简支桥梁上运行引起的车桥动力响应。
1模型的建立
用移动质量模拟车辆匀速通过跨度为32m简支梁的情形,采用ANSYS软件建立相应模型,对桥梁的动力响应进行仿真计算。计算中,模型忽略桥梁粗糙、不平顺的影响,不考虑外界风载及地震荷载的影响,不考虑车的初始状态,即认为车辆在理想的状态下运行通过桥面。
本文采用二维梁单元BEAM3来模拟桥梁,划分的单元数由荷载的移动速度和桥梁长度来决定。单元长度△L=L/N,其中,L为桥梁的跨长,N为划分的单元数。这样,荷载在单元之间的运行时间(即从i节点变化到i+1节点)为t=△L/v,其中,口为移动荷载的速度。计算时,划分单元数为50。

在计算结构动态响应时,时间步长△t的选取是否合适,对计算结果能否反映结构响应特征产生很大的影响。如果时间步长△t太大,有可能得到完全失真的响应曲线。在图1所示的响应曲线中,如果步长不当,将会得到如虚线所示的错误的响应曲线。
时间步长的选取,应根据动态响应的振动周期频率来确定。由于三点确定一条抛物线,因此为了真实描述结构动态响应,在一个振动周期中应至少取5个点。如果设T是结构振动的周期,是结构振动的频率,那么结构动态响应计算的时间步长应取为
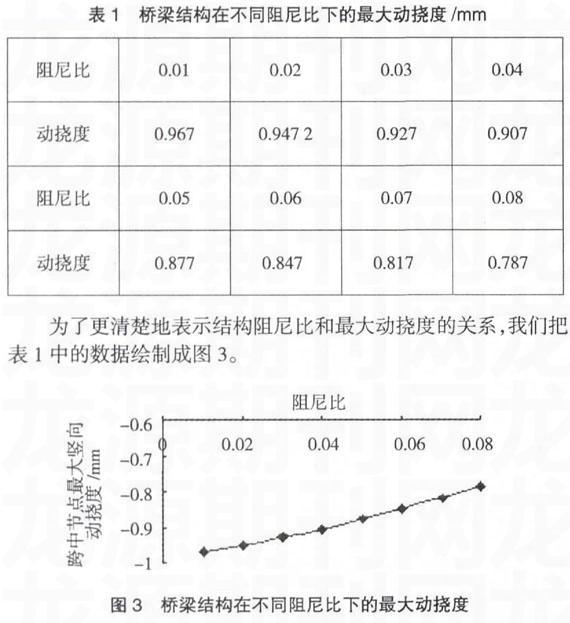
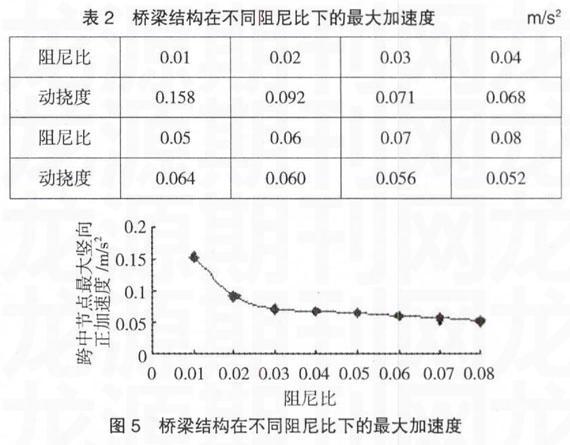
△L (1) 本文采用桥梁模型基准数据如下:简支梁跨度1=32m,连续梁跨度l=64m,材料为50号混凝土,弹性模量E=3.5×1010N/m2。箱型断面,断面高度2.8m,断面宽度13m,截面积为A=8.29m2。惯性矩I=8.6m4,密度p=2500kg/m3。 本文主要研究不同阻尼比的桥梁结构的动力性能(阻尼比变化范围为0.01~0.08),采用的基准车速为300km/h。3数值模拟及结果分析 图2表示了结构阻尼比为0.02、0.04、0.06、0.08时桥梁跨中节点的动挠度曲线。由图2可知,对于高速运行的车辆,随着梁上阻尼比的增加,梁上节点的动挠度逐渐减小。另外,随着梁上阻尼比的增加,各节点发生最大动挠度时荷载所在地位置逐渐后移。表1详细记录了阻尼比由0.01~0.08范围内桥梁跨中节点的最大竖向动挠度。 图3为表1数据所绘,从图中我们不难看出最大动挠度与结构阻尼比的关系已不再是线性的而变为非线性的。结构阻尼比越大,跨中节点的最大动挠度越小。 图4表示了结构阻尼比为0.02、0.04、0.06、0.08时桥梁跨中节点的竖向加速度曲线。可以看出,各节点的竖向加速度表现出类似于正弦曲线特性,随着阻尼比提高,其向下的竖向加速度明显减小。但是在一定范围内,随着阻尼比的提高,其向上的竖向及速度并没有明显减小。由此可见,通过适度提高结构阻尼比的方法可以在一定程度上控制桥梁结构的振动。 图5是由表2数据所绘,详细列出了结构在不同阻尼比下跨中节点的竖向加速度情况,从中不难看出,结构的竖向加速度和结构的阻尼比的关系不再是线性的,而变为非线性的。在结构阻尼比不大的时候,随着阻尼比的提高,结构的竖向加速度降低的速度比较快。随着结构阻尼比的增加,这种影响作用会越来越小。所以,在一定范围内控制结构阻尼比可以很好地控制桥梁结构的震动。 3结论 本论文采取了数值模拟计算的研究方法。对移动质量作用下桥梁的动态响应做了分析研究。通过ANSYS软件对车一桥藕合系统的动态模拟,得到桥梁的动力响应结构阻尼比的关系,通过数据分析得出如下结论: (1)桥梁结构在高速列车作用下的动挠度与结构阻尼比之间并非是线性的关系,但总体规律是随着结构阻尼比的增加,桥梁结构的动挠度逐渐减小。 (2)随着阻尼比的增加,桥梁结构的向下加速度明显减小,但是在一定范围内,随着阻尼比的提高,其向上的竖向及速度并没有明显减小。由此可见,通过适度提高结构阻尼比的方法可以在一定程度上控制桥梁结构的振动。