完全图K2n+1的2-因子分解
2009-12-04霍玉洪淮南师范学院数学与计算科学系安徽淮南232038
霍玉洪 (淮南师范学院数学与计算科学系,安徽 淮南 232038)
侴万禧 (安徽理工大学土木建筑学院,安徽 淮南 232001)
完全图K2n+1的2-因子分解
霍玉洪 (淮南师范学院数学与计算科学系,安徽 淮南 232038)
侴万禧 (安徽理工大学土木建筑学院,安徽 淮南 232001)
以奇阶完全图K2n+1的1-因子分解为基础,研究了奇阶完全图K2n+1的2-因子分解问题,给出了奇阶完全图K2n+1和2-因子分解的具体步骤以及H圈的具体构造方法,并以K13为具体实例进行了分析研究。
完全图;因子分解;奇阶;H圈;矩阵
1 基本引理
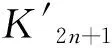
引理2[7,8]设完全图K2n+1的Δ(G)+1个1因子为E(G1),E(G2),…,E(GΔ(G)+1),则K2n+1的2-因子分解可归纳为Δ(G)+1个1因子E(G1),E(G2),…,E(GΔ(G)+1),并为n个H圈的边集E(C1),E(C2),…,E(Cn)。
2 2-因子分解
设G为完全图K2n+1,由引理1可得K2n+1的1-因子分解步骤如下:

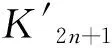
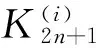
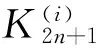
E(C1)={12,22n,42n,42n-2,…,52n-1,32n-1,32n+1,12n+1}
E(C2)={13,32n-2,72n-2,42n-3,…,52n,12n}
E(C3)={14,46,62n,102n+1,…,23,32n-2,72n-1,12n-1}
…
E(Cn)={1n+1,2n+1,2n,3n,…,82n,82n+1,72n+1,1n+2}
3 实 例
下面以K13为例来具体分析分解步骤。
K13的2-因子分解决定于K13的Δ(G)+1=13个1因子E(G1),E(G2),…,E(G13),而13个1因子E(G1),E(G2),…,E(G13)的构造步骤如下:

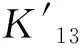
K13的n=6个H圈的边集E(C1),E(C2),…,E(C6)的构造步骤如下:
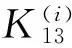
E(C1)={12,212,412,410,610,68,78,79,59,511,311,313,113}
E(C2)={13,310,710,67,611,211,213,413,49,89,58,512,112}
E(C3)={14,48,810,210,23,39,69,612,1213,513,57,711,111}
E(C4)={15,56,613,1113,811,38,312,712,47,24,29,910,110}
E(C5)={16,46,34,37,713,1013,510,25,28,812,1112,911,19}
E(C6)={17,27,26,36,35,45,411,1011,1012,912,913,813,18}
[1]刘振宏.应用组合论[M].北京:国防工业出版社,1993.
[2]孙淑玲,许胤龙.组合数学[M].合肥:中国科学技术大学出版社,1999.
[3]杨烨飞,王朝瑞.组合数学及其应用[M].北京:北京理工大学出版社,1992.
[4]Fred S Roberts,Barry Tesmar.Apllied Combinatorics[M].Beijing:China Machine Press,2007.
[5]卢开澄,卢华明.组合数学[M].北京:清华大学出版社,2006.
[6]van Lint J H,Wilson R M.A Course in Combinatorics[M].Beijing:China Machine Press,2004.
[7]侴万禧.2n名选手循环赛安排问题[J].数学的实践与认识,2006,36(2):252~256.
[8]侴万禧.2t名运动员的循环赛和对集的划分[J].安徽理工大学学报(自然科学版),2006,26(1):64~69.
[编辑] 洪云飞
O157.5
A
1673-1409(2009)02-N016-03
2009-03-07
安徽省2009年高等学校省级自然科学研究项目(KJ2009B269Z);淮南师范学院2007年度青年科研基金资助计划项目资助(2007Lkp05)。
霍玉洪(1976-),男,2000年大学毕业,硕士,讲师,现主要从事应用数学及图论方面的研究工作。
