关于数学解题教学的思考

李凤忠

关键词:模仿;变式;领悟;分析

中图分类号:G633.6 文献标识码:B

文章编号:1009-010X(2009)09-0063-02

波利亚在《怎样解题》一书中指出:“一个好的教师应该懂得并且传授给学生下述看法:没有任何问题是可以解决得十全十美的,总剩下些工作要做,经过充分的探讨与钻研,我们能够改进这个解答,而且在任何情况下,我们总能提高自己对这个解答的理解水平。”这就说明,分析解题过程不仅能“改进”解答,而且能提高“理解”水平。

一、简单模仿——学会解题的初步体验

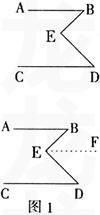
例:如图,AB∥CD,求证:∠B+∠D=∠BED

分析:(1)为了证明两个角的和等于一个角,需要建立这三个角之间的联系。

(2)由于已知条件只有一个AB∥CD,所以作辅助线EF∥AB,产生了AB∥CD∥EF(如图1),把∠BED分成两个角,与∠B和∠D也建立了联系。

(3)证明∠B=∠BEF,∠D=∠DEF;∠B+∠D=∠BEF+∠DEF=∠BED。

(4)由平行线的性质得出内错角相等,得出证明结论

证明一:如图1,作EF∥AB,因为 AB∥CD,所以 EF∥CD;所以,∠B=∠BEF,∠D=∠DEF;所以,∠B+∠D=∠BEF+∠DEF=∠BED。

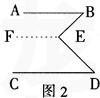
评析:上述处理有分析、有启引,注重了知识的发生过程,几何论证能力在潜移默化中得到提高。这时我们要让学生模仿证明方法,探索新的解法。

学生通过模仿探究出如图2的解法,运用两直线平行,同旁内角互补知识,得出证法二:作EF∥AB,因为AB∥CD,

所以EF∥CD;所以,∠B+∠BEF=180°,∠D+∠DEF=180°;又因∠BEF+∠DEF+∠BED=360°,所以,∠B+∠D=∠BED。

二、变式练习——主动实践与应用

引导学生分析题中已知条件,观察图中的线段,借助“有用捕捉、有关提取、有效组合”,得出如下信息:

证法三:如图3:延长BE交

CD于F。则∠BED=∠EFD+∠D;又因AB∥CD,所以,∠B=∠BFD;所以∠BED=∠B+∠D。

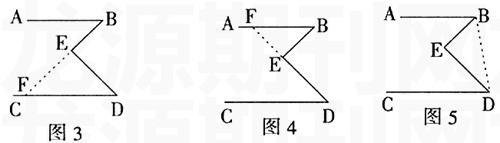
证法四:如图4:延长DE交AB于F。与证法三类同。

证法五:如图5:连接BD,则∠BED+∠EBD+∠BDE=180°;又因为AB∥CD,所以∠ABE+∠EBD+∠BDE+∠EDC=180°;

所以∠BED=∠ABE+∠EDC。

评析:上述三种证明方法通过作辅助线,构造出了三角形,再借助平行线的性质,建立了∠BED和∠B、∠D的联系,学生易于掌握并得出证明方法。

三、自发领悟——解题后的再思考

在平时的教学活动中,我们会到此为止,认为思路已经打通,学生都想出5种证法了,还有什么不满足的呢?如果此时此刻,忽视解题后的再思考,也就错过提高的最好机会,应对学生加以引导,是否从上面的几种证法中,将某些线段进行平移,得出新的证法?

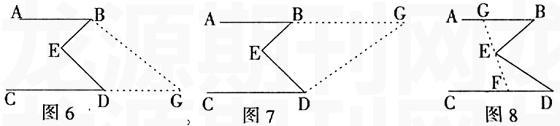
通过引导学生观察图形,组织学生探索、交流,得出将图4中的线段DF向右平移,使点F与点B重合,交CD的延长线于G。

证法六:如图6,由平移得到BG∥ED,则∠CDE=∠G;∠BED+∠EBG=180°;又因AB∥CD,则∠ABE+∠EBG+∠G

=180°;即∠ABE+∠G=∠ABE+∠D=180°-∠EBG;所以,∠BED=∠ABE+∠EDC。

证法七:如图7,将图3中的线段BF向右平移,使点F与点D重合,交AB的延长线于G,下面证法同证法六。

证法八:如图8,将图5中的线段BD向左平移至GF,使点E在GF上;这样构造出了△BGE和△DFE,则由三角形内角和定理得到:∠B+∠BGE+∠BEG=180°,∠D+∠DEF+∠DFE=180°,所以∠B+∠D=360°-∠BGE-∠BEG-∠DEF-

∠DFE=360°-(∠BGE+∠DFE)-(∠BEG+∠DEF)又因AB∥CD,∠BGE+∠DFE=180°;而∠BED=180°-(∠BEG+∠DEF)所以∠BED=∠B+∠D。

评析:上述三种证法通过平移线段得到新的方法,仍然是建立∠BED和∠ABE、∠EDC三者之间的联系,使探究问题得到升华。教师的主导作用就在于相机引导,使学生处于“愤”、“悱”状态,发展学生的发散思维能力,有效地激发了学生的学习兴趣,培养了学生的创新精神,领悟了平面几何证明题的魅力。

四、自觉分析——暴露数学思维的过程

对解题过程进行自觉的反思,使理解进入到深层结构,这是一个通过已知学未知、通过分析“怎样解题”而领悟“怎样学会解题”的过程,也是一个理解从自发到自觉、从感性到理性、从基础到创新的飞跃阶段。

让学生审视上述几种证明方法,证法一、二、三、四、八作的辅助线均过E点,看看哪位同学有新的发现?学生通过自觉反思,合作交流得到如下的证明方法:

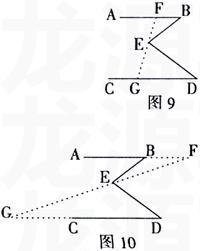
证法9:顺时针转动图8中的线段GF,得到图9,其证法与证法八类同。

证法10:继续顺时针转动图中的线段GF,当GF与EB重合时(和证法三同),继续转动得到图10。

因为∠ABE=∠F+∠BEF,∠FED=∠G+∠D;又因AB∥CD,所以∠F=∠G,∠ABE+∠G+∠D=∠F+∠BEF+∠FED=∠F+∠BED,即∠BED=∠ABE+∠D。

继续顺时针转动图10中的线段GF,当GF与AB、CD没有交点时,情况是怎样的?同学们一个个摩拳擦掌,跃跃欲试,得出GF∥AB∥CD(这样就归结到了证法一、二),让学生感受了极限思想。

评析:通过转动过E点的辅助线,实现了上述几种证法的有机统一,使学生认识到只要作过E点的直线即可得到证明方法。这是因为有了这条线,就建立起了∠BED和∠ABE、∠EDC的联系;本课例的数学对象是生动有趣的,学生的学习活动也是积极活跃的。一题多解是培养学生创新能力的有效途径。由静止到运动,开阔了学生的视野,感悟了问题解决的美妙。

《数学课程标准》要求数学教学是数学活动的教学,需要学生用内心的体验与创造的方法来学习数学,教师应创设有利于学生生动活泼、主动发展的情境,让学生亲历探究过程。只有这样,教师才能成为学生学习的引导者、组织者与合作者。